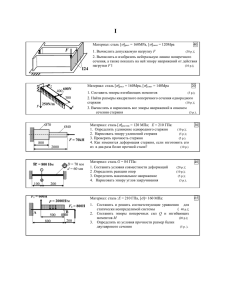
Изобразим стержень с одной опорой (правой), соблюдая

Методическое пособие к выполнению задания № 2
Рассмотрим № 00.
С х е м а I (кручение)
M 1  2 kHм,
М 2  3 кНм ,
М 3  4 кНм ,
Дано:
а  0,2 м;
D / d  1,2;
b / d  1,1;
h / b  1,3 .
   100 МПа ,
G  8  10 4 МПа .
1. Построение диаграмм крутящих моментов М КР и углов закручивания  для
стержня без одной опоры (правой или левой).
Решение:
Изобразим стержень с одной опорой (правой), соблюдая масштаб линейных величин. Диаграммы строятся на осях параллельных оси стержня с проставлением значений ординат в характерных точках и также с соблюдением масштаба.
Реактивный момент в опоре определяется из уравнения равновесия системы: сумма моментов относительно оси Х равна нулю (ось Х – ось стержня).
m X  M A  M 3  M 1  M 2  0 ;
M A  M 3  M 1  M 2  4  2  3  3 kHм .
2
Определение (внутренних) крутящих моментов
Внешние скручивающие моменты (сосредоточенные) разделяют стержень на
силовые участки, в сечениях которых внутренние моменты определяются из
уравнений равновесия какой-либо части стержня (правой или левой) образуемой сечениями 1, 2, 3 (см. схему стержня).
Сечение 1. (выделяем правую часть)
0  х  1,5 а
(Сечение перемещается от М 2 до М 1 )
Правило знаков для крутящих моментов:
Момент считается положительным, если при
взгляде со стороны нормали на поперечное сечение, он направлен против хода часовой стрелки.
Крутящий момент определяется из уравнения равновесия:
 m X  М КР  М 2  0 ;
Обычно уравнение равновесия в таком виде не записывается, а формируется
M КР   М 2  3 кНм .
сразу результат следующий из него
Последняя запись очевидна, если в сечении изображать внутренний момент
М КР в положительном направлении, а в правой части уравнения (как результат) записывать внешние моменты, ориентируясь на его знак.
Как видим, М КР не зависит от текущей координаты х и распределение
его по соответствующей длине линейно.
Соответственно указанным пределам изменения х отображаем уравнение
графически на диаграмме М КР .
Аналогичным образом поступаем с другими частями стержня.
Сечение 2 (правая часть):
M КР
0  х  1,5 а
  М 2  М 1  3  2  1 кНм
Сечение 3 (левая часть):
0  х  0,5 а
M КР  М А  3 кНм .
3
Построение диаграммы углов закручивания
Для определения поворота одного сечения стержня относительно другого, удалённых друг от друга на расстояние  , исходным является выражение
М 
   КР .
закона Гука:
G  JP
Эта формула действительна только для части
стержня постоянного сечения на длине  .
Произведение G  J P называется жесткость
стержня при кручении, J P - полярный момент
инерции поперечного сечения стержня.
 d4
Для сплошного круга:
.
JP 
32
4
  D4   d 4   D4   d  
JP 


 1     .
Для кольцевого сечения:
32
32
32
  D  
Для прямоугольника вместо полярного момента инерции введено понятие геометрического параметра (фактора) жесткости J K , который по смыслу эквивалентен полярному моменту инерции сечения. Выражение его получено методами теории упругости:
J K  J P    b3  h
При формулировании условия прочности при кручении используются
геометрические характеристики, которые называются полярными моментами
сопротивления, и находятся они по определению:
JP
WP 
.
 МАХ
Для сплошного круга
 d3
 МАХ  d / 2 :
.
WP 
16
Для кольцевого сечения
4
  D3   d  
 МАХ  D / 2 :
WP 
 1     .
16
  D  
Для прямоугольного сечения используется геометрический параметр эквивалентный по смыслу полярному моменту сопротивления:
WK  WP    b 2  h .
Коэффициенты  и  зависят от отношения сторон h b и определяются
по таблице. Следует обращать внимание на то, что b есть малая сторона прямоугольника.
Ниже приведён фрагмент этой таблицы и показана графически операция
определения этих коэффициентов для отношений сторон не включённых в таб-
4
лицу. Эта операция называется интерполирование. Считается, что в промежутке межу табличными значениями изменение идёт по линейному закону.
Можно эти коэффициенты определять аналитически по выражениям, которые непосредственно следуют из графического представления операции.


0,196  0,141
 0,3  0,174 .
0,5
0,5
 1,5   1,0
0,231  0,208
 1,3   1,0 
 0,3  0,208 
 0,3  0,2218 .
0,5
0,5
Определим геометрические характеристики поперечных сечений стержня, выразив их размеры через один определяющий параметр (н/п, d ), используя
заданные соотношения между размерами.
Введём нумерацию характеристик, чтобы в дальнейшем с ними не запутаться.
Прямоугольник: b  1,1  d ; h  1,3 b  1,3  1,1  d  1,43  d ;

1,3  
1,0

1,5
1, 0
 0,3  0,141 
J 1  0,174  1,1  d 3  1,43  d  0,3312  d 4 ,
W1  0,2218  1,1  d 2  1,43  d  0,3838  d 3 .
Кольцевое сечение:
D  1,2  d ;
4
  1,2  d 4   1  
J2 
 1      0,1054  d 4 ;
32
  1,2  
4
  1,2  d 3   1  
W2 
 1      0,1757  d 4 .
16
  1,2  
 d4
 d3
4
J2 
  0,0982  d ;
W2 
  0,1963  d 3 .
Круг:
32
16
Определим повороты сечений для частей стержня, где крутящие моменты и
жесткости постоянны по длине:
Поворот сечения 1 относительно А:
5
1 / A 
3  10 3  0,1
 1,132  10 8 
1
 м4
8  10  0,3312  d
d
Поворот сечения 2 относительно 1:
 1  10 3  1,5  0,2
1
8
 2 /1 


3
,
558

10

 м4
10
4
4
8  10  0,1054  d
d
Поворот сечения 3 относительно 2:
 3  10 3  0,1
1
8
3/ 2 


3
,
558

10

 м4
10
4
4
8  10  0,1054  d
d
Поворот сечения 4 относительно 3:
 3  10 3  0,2
1
8
4
4/3 


7
,
637

10


м
8  1010  0,0982  d 4
d4
Поворот концевого сечения 5 относительно 4:  5 / 4  0 .
По вычисленным значениям углов определяются повороты всех сечений относительно неподвижного сечения А. Так, поворот освобождённого конца равен:
 5 / A  1 / A   2 / 1   3 / 2   4 / 3   5 / 4 .
Процедура вычислений показана на диаграмме углов закручивания.
10
4
4
2. Построение диаграммы М КР для стержня с двумя опорами.
Статика даёт одно уравнение равновесия при двух неизвестных моментах в
опорах:
m X  M A  М В  M 3  M 1  M 2  0 .
Задача статически неопределима. Дополнительное уравнение можно записать,
учитывая, что в опорах стержня его сечения не поворачиваются.
Устраним правую опору, заменив её действие моментом Х. Очевидно
этот момент будет равен реактивному М В , если поворот сечения равен нулю.
Дополнительное уравнение:  В  0 .
Определяем угол поворота на основании принципа суперпозиции:
M  0,5a  M 1  0,5a M 1 1,5a   M 2  0,5a M 2  2a M 2  a 
 
  
В  3
 



G  J1
G

J
G

J
G

J
G

J
G

J

1
2  
1
2
3 
 X  0,5a X  2a X  2a 
  0
 


G

J
G

J
G

J
1
2
3 

Находим момент:
J1 
J
J 
  M 2  0,5  M 2  2  1  M 2  1 
J2 
J2
J3 
;
J1
J1
0,5  2 
 1,5 
J2
J3
 M 3  0,5  M 1  0,5  M 1  1,5 
X
6
0,3312 
0,3312
0,3312 
  3  0,5  3  2 
 3

0,1054 
0,1054
0,0982 
X
 1,524 kHм .
0,3312
0,3312
0,5  2 
 1,5 
0,1054
0,0982
Примечание: для определения момента Х можно воспользоваться выше
найденным углом поворота концевого сечения стержня с одной опорой:
X  0,5a X  2a X  1,5a


 5/ A  0 ,
G  J1
G  J2
G  J3
1
 13,621  10 8 4
d
X 
 1,524 кНм .
1
1  0,1
2  02 1.5  0,2 





8  1010 d 4  0,3312 0,1054 0,0982 
Возвращаясь к уравнению равновесия, определяем момент в опоре А:
M A  М В  M 3  M 1  M 2  1,524  4  2  3  4,524 kHм .
После определёния моментов в опорах строится диаграмма М КР .
 4  0,5  2  0,5  2 1,5 
7
3. Подбор размеров поперечных сечений стержня из условия прочности.
М
 МАХ  КР   
Необходимо обеспечить условие прочности:
WP
и соотношения между параметрами поперечных сечений частей стержня.
Определим размеры прямоугольного поперечного сечения, исходя их того, что в этой части M КР МАХ  4,524 кНм .
М КР МАХ
0,3838  d
3
   ;
d
3
Примем d  5  10 2 м  50 мм .
Размеры прямоугольного сечения:
 МАХ 
С этими размерами
4,524  10 3
0,3838  100  10
6
 4,903  10 2 м .
b  1,1  50  55 мм , h  1,43  50  71,5 мм
4,524  10 3

0,3838  5  10

2 3
 94,3 МПа .
Недогрузка составляет 5,7%
Проверим прочность кольцевого сечения: D  1,2  50  60 мм :
 МАХ 
1,476  10 3


2 3
 67,2 МПа   .
0,1757  5  10
Проверим прочность круглого сечения:
1,524  10 3
 МАХ 
 62,12 МПа    .
2 3
0,1963  5  10
Примечание: Если не удовлетворяется условие прочности для какой-либо части
стержня, необходимо его обеспечить для неё, определив необходимые размеры,
затем по ним назначить размеры других сечений и проверить их прочность.


4. Построить диаграмму углов закручивания для стержня с двумя опорами.
Поворот сечения 1 относительно А:
4,524  10 3  0,1
1
8
1 / A 

1
,
707

10

 м4
10
4
4
8  10  0,3312  d
d
Поворот сечения 2 относительно 1:
0,524  10 3  1,5  0,2
1
8
 2 /1 

1
,
864

10

 м4
10
4
4
8  10  0,1054  d
d
Поворот сечения 3 относительно 2:
 1,476  10 3  0,1
1
8
4
3/ 2 


1
,
7505

10


м
8  1010  0,1054  d 4
d4
Поворот сечения 4 относительно 3:
 1,476  10 3  0,2
1
4/3 
 3,7574  10 8  4  м 4
10
4
8  10  0,0982  d
d
8
Поворот концевого сечения 5 относительно 4:
1,524  10 3  0,1
1
5/ 4 
 1,9093  10 8  4  м 4
10
4
8  10  0,0982  d
d
Проверка: поворот сечения В (или 5) равен
10 8
10 8
 В  (1,707  1,864  1,751  3,757  1,909)  4  0,028  4 .
d
d
Погрешность 0,5%.
По вычисленным значениям строится диаграмма (см. схему). Величины углов в
радианах находятся при замене диаметра d его числовым значением и в градусах умножением:  о    рад   180 о /  .
5. Рассчитать опорные закрепления стержня с двумя опорами (сварка).
Касательные напряжения в сварном шве образуют опорные моменты, которые уравновешивают крутящие моменты в примыкающих к опорам сечениях
стержня.
В левой опоре усилия T1    0,7  t  b и T2    0,7  t  h образуют момент
h
b

M A  2   T1   T2      0,7  t  b  h  b  h     0,7t  2 Aпр .
2
2

В правой опоре момент образуют напряжения, распределённые по кругу:
 d
d
 d2
M B   (  0,7t  d)     0,7 
   0,7t  2 Акр .
2
2
0
9
Апр , Акр - площади, ограниченные контуром поперечных сечений стержня..
Это не площади поперечных сечений стержня, которые могут быть полыми.
Напряжения в швах:
MA
MВ
,
 пр 
 кр 
0,7t  2 Апр
0,7t  2  Акр
Можно заметить, что эти площади следует определять по средней линии шва:
  d  t / 22
*
*
Акр  2 
.
Апр  2  b  t / 2  h  t / 2 ,
4
Из условия     прочности определяется толщина шва.
Для прямоугольника:
MA
4,524  10 3
t пр 

 8,2  10 3 м  8,2 мм .

6
6
0,7  2bh    1,455  71,5  10  100  10
Для круга:
MВ
1,524  10 3
t кр 

 5,54  10 3 м  5,54 мм
2
2
3
 d
0,7  2
   1,4  3,14  50  10
 100  10 6
4
4
Расчет очевидно приближенный, чтобы не решать квадратные уравнения, которые будем иметь, если использовать А * . Его можно уточнить и назначить
толщину швов несколько меньше полученных значений.
Примем t пр  7,5 мм, t кр  5 мм . При этом напряжения:

 пр 
 кр 
МА
*
1,4  t  Апр
МВ



4,524  10 3
1,4  7,5  10 3  55  3,75 71,5  3,75   10 6
4  1,524  10 3
1,4  5  10  3,14  50  2,5  10
Этим результатом можно удовлетвориться.
1,4  t 
*
Акр
3
2
6
 97,46 МПа .
 100,57 МПа .
10
Схема II. (Изгиб двухопорной балки)
Дано: а  1,5 м, b  2 м, с  3м, М  20кНм, q  10kHм .
   160 МПа ,
Е  2,110 5 МПа .
1. Построение диаграмм поперечных сил Т и изгибающих моментов М И .
Следует соблюдать масштаб изображаемых величин.
Реакции:
 a  2b  c

m A  R B  2b  P  2b  c   M  q  a  2b  c   
 a  0 ,
2


 1,5  2  2  1,5

 15  2  2  3  20  10  1,5  2  2  3  
 1,5 
2

  37 ,19 kH
RB 
.
22
 a  2b  c

m B  R A  2b  P  c  M  q  a  2b  c   
 c  0 ,
2


 1,5  2  2  1,5

15  3  20  10  1,5  2  2  3  
 3
2


RА 
 32,81 kH .
22
11
Проверка: Y  R A  R B  P  q  a  2b  c   32,81  37,19  15  10  8,5  0 .
Построение диаграмм Т и М И .
В поперечных сечениях стержня внутренние силовые факторы следует изображать в положительном направлении, согласно принятому правилу знаков:
Знак момента М И принят по знаку кривизны, знак поперечной силы Т по знаку
касательных напряжений.
Сечение 1. (правая часть)
0  х  с  3м ,
mC  0 следует
Из уравнений равновесия: Y  0,
T   P  q  x  15  10  х , (прямая)
q  х2
10  х 2
. (парабола)
MИ  P х 
 15  х 
2
2
Парабола имеет экстремум (максимум или минимум),
где её производная равна нулю.
P 15
dM
 T  0   P  q  x 0 , x 0    1,5 м
dx
q 10
10 1,5 2
( М И )хо  15 1,5 
 11,25кНм .
2
Вначале следует построить диаграмму Т , затем, видя распределение касательных функции М И , изобразить её.
Результаты вычислений, по которым строятся диаграммы, рекомендуется
представлять таблицей.
0  х  2b  4 м ,
Сечение 2. (правая часть)
Координату сечения отсчитываем от опоры.
12
T   P  R B  q  с  х   15  37,19  10  c  x   42,19  10  3  x  ,
q   x  c 2
10  3  x 2
M И  P  c  x   R B  x 
 15  3  x   37,19  x 
.
2
2
Текущую координату сечения можно отсчитывать от конца стержня.
При этом:
c  х *  c  2b ,
T   P  R B  q  х  15  37,19  10  х  42,19  10  х ,
MИ
q  х2
10  х 2
.
 P  х  RB  х  с 
 15  х  37,19   х  3 
2
2
Сечение 3. (левая часть):
0  х  а  1,5м ,
T  q  х  10  х
MИ
q  х2
10  х 2
.


2
2
Для самоконтроля правильности построения диаграмм:
на диаграмме Т наблюдаются разрывы (скачки) функций в месте сосредоточенных сил, равные значениям этих силам. На диаграмме М И сосредоточенный момент изображён также соответствующим разрывом функций, сосредоточенные силы точкой излома (изменение угла наклона касательной).
2. Изображение изогнутой оси балки.
Без количественной оценки перемещений поперечных сечений балки её изогнутую ось изображаем по распределению изгибающих моментов по длине,
зная, что в шарнирных опорных устройствах возможен поворот и линейные перемещения отсутствуют (если опоры не перемещаются), а в защемлении отсутствуют оба перемещения. Необходимо учитывать: положительному моменту
соответствует положительная кривизна и наоборот; смена кривизны (точка
перегиба), где изгибающий момент равен нулю; кривизна там больше, где
больше изгибающий момент.
3. Определить размеры поперечного сечения стержня из условия прочности:
13
МИ
 y МАХ    .
JZ
Геометрические характеристики поперечного сечения.
Изгиб осуществляется относительно главной центральной оси Z, положение которой необходимо определить.
Сечение образовано из двух элементарных фигур: прямоугольника и полукруга,
для которых геометрические характеристики обычно известны:
2b  b 3
,
A1  2b  b, y c1  0,5b;
J z1 
12
  r 2   0,8b 2
4  r 4  0,8b
A2 

,
y c2 

,
J z2  0,1098  r 4  0,1098  0,8b 4
2
2
3
3
Определим положение центра тяжести всего сечения относительно вспомогательной оси (см. рисунок):
  0,8b 2 4  0,8b

A1  y c1  A  y c2 2b  b  0,5b 
2
3    0,6552  b .
yC 

A1  A2
  0,8b  2
2b  b 
2
Момент инерции сечения относительно оси Z определяется как алгебраическая сумма моментов инерции элементарных фигур приведённых к этой
оси:
 2b  b

J Z  J z1  a12  A1  J z2  a 22  A2  
 0,6552b  0,5b 2  2b 2  
 12

2

4  0,8b    0,8 2 

4
4
 0,1098  0,8b    0,6552 b 
  0,0697  b .
 
3 
2



Определение размеров поперечного сечения
Для стержня постоянного сечения по длине расчетная величина изгибающего
момента есть максимальное его значение (по модулю) на диаграмме. Сечение с
максимальным значением момента называется "опасным". В нашем случае:
М мах РАСЧ  24,61 кНм ,
Знак показывает, что верхняя часть сечения (выше нейтральной оси Z ) сжимается, нижняя часть растягивается. Координаты точек сечения наиболее удалённых от нейтрального слоя находятся в растянутой зоне:
 у МАХ Р  0,6552  b
Из условия прочности:
M max  P
JZ
0,0697  b 3

 0,1064  b 3 
,
 
YMAX  P 0,6552  b
 МАХ 

b3
 
24,61  10 3
0,1064  160  10 6

 11,309  10 2 м .
Принимаем b  11,3 см
14
Диаграмма распределения нормальных напряжений по высоте сечения.
Нормальные напряжения изменяются по линейному закону:
М
у  И y
JZ
Для построения диаграммы достаточно определить напряжения в двух точках
(максимально удалённых от нейтральной оси Z ):
М МАХ
24,61  10 3
 МАХ  Р 
 0,6552  b 
 0,6552  160,3 МПа
2 3
0,0697  b 4
0,0697  11,3  10
М МАХ
24,61  10 3
 МАХ С 
 (1  0,6552 )  b 
 0,3448  84,4 МПа
2 3
0,0697  b 4
0,0697  11,3  10
Диаграмма распределения касательных напряжений по высоте сечения.




Касательные напряжения определяются по формуле Журавского:
T  S Z ОТС
у 
, где
J Z  by
 у - напряжения на уровне у удалённого от
нейтральной оси Z ,
S Z ОТС - статический момент площади выше
уровня у или ниже:
S Z ОТС  АОТС   уС ОТС ,
b y - ширина сечения (по материалу) на уровне у .
Точки, в которых необходимо определить напряжения, указаны цифрами на
поперечном сечении балки.
В наиболее удалённых точках поперечного сечения касательные напряжения
отсутствуют. Точка 1 и 4: S Z ОТС  0,  1  0,  4  0 .
Точка 2:
Аотс  0,4  b 2 ,
y c  0,2448  b .
Напряжения определяем в сечении, где
сдвигающая сила имеет максимальное
15
значение.
По диаграмме Т MAX  22,19 kH .
T  ( S Z ) отс2 Т  0,4  b 2  0,3548  b 22,19  10 3  0,4  0,3548
2 


 1,72 МПа
J Z  bу
0,0697  b 4  2  b
0,0697  (11,3  10 2 ) 2  2
Точка 3:
( S Z ) отс3  А1  у с1  А2  у с2 .
Необходимо определить площадь сегмента и положение его центра тяжести.
Площадь сегмента находится как разность площади сектора с центральным
углом ( 2   ) и треугольника:
А

180
  r 2  h  r 2  h2 ,
h
r
Положение центра тяжести относительно центра круга:
S
yc  Z ,
A
Статический момент площади сегмента относительно оси, проходящей через
центр круга:
r
3
2
S Z   y  dy   y  2 r 2  y 2  dy   r 2  h 2 2 .
3
A
h
В нашем случае: r  0,8  b, h  0,6552  b .
3/ 2
2
S Z  0,8 2  0,6552 2
 b 3  0,0645  b 3 .
3
0,6552
  arc cos
 35 0 ,
0,8
35
A2 
 3,14  0,8  b 2  0,6552  b  0,8 2  0,6552 2  b  0,0902  b 2
180
0,0645
yc 
 b  0,718  b .
0,0902
  arc cos .




16
у с2  у с  h  0,718  0,6552   b  0,00566  b .
b y  2  b  0,8 2  0,6552 2  b  1,082  b .
0,3448


T   2  0,3448  b 2 
 b  0,0902  b 2  0,00566  b 
2

3  

0,0697  b 3  1,082  b

22,19  10 3  0,1184

0,0697  11,3  10

2 2
 1,082
 2,73 МПа .
Схема III. (Изгиб консольной балки)
1. Построение диаграмм поперечных сил Т и изгибающих моментов М И .
Реакции определяются из уравнений равновесия:
Y  R A  P  q  a  q  b  c   0 ,
R A   P  q  a  q  b  c   15  10  1,5  10  2  3  20 kH .
a
b  c

m A  M A  M  P  a  b   q  a   q  b  c   
 a  0,
2
 2

17
a
b  c

 q  b  c   
 a,
2
 2

1,5 2
23

M A  20  15  1,5  2  10 
 10  2  3  
 1,5   116,25 kHм .
2
 2

Как и для схемы II осуществляется построение диаграмм внутренних сил.
Заметим, что реакции можно не определять, если при определении внутренних
сил на участках рассматривать правую часть стержня (перемещаться от свободM A   M  P  a  b   q  a 
ного конца: сечения 4-3-2-1). Значение реакций можно увидеть на диаграммах.
3.Подбор размеров поперечного сечения балки из условия прочности.
Геометрические характеристики поперечного сечения.
Сечение имеет две оси симметрии и положение главных центральных осей известно.
Момент инерции сечения относительно главной центральной оси Z:
2


a

a

J Z  4   J z1    b  y c   A , y MAX    b  .
2

2



Осевой момент сопротивления сечения определяется выражением:
J z  a 2  b  y c   A
J
.
WZ  Z  4  1
y MAX
a 2b
По условию прочности требуемый момент сопротивления:
M И РАСЧ 116,25 103
WZ 

 7,266  10 4 м3  726,6 см3
6
 
160  10
J z1  a 2  b  y c  2  A
4
 726,6 см 3 ,
Получаем уравнение:
a 2b
которое решается подбором (последовательными приближениями).
Назначим неравнополочный уголок №11/7, для которого из сортамента
проката находим:
А  13,9 см 2 , t  0,8 см, В  11 см, b  7 cм, у с  1,64 см, J z1  54,6 см 4




18
Следует обратить внимание на обозначение осей в сортаменте и принятое в
расчёте.
Уравнение получает вид:
4  54,6  а / 2  7  1,64 2  13,9
3
 726,6 см
a/27
Примем а  20 см :




4  54,6  10  7  1,64  2  13,9
3
 784,5 см (существенное превышение требуе10  7
мого значения).
Уменьшим размер а  18 см :


4  54,6  9  7  1,64  2  13,9
3
 730,2 см .
97
726,6  730,2
Недогрузка:
 100  0,5% .
726,2
С последним результатом:
J Z  W Z  y MAX  730,2  16  116,83  10 2 cм 4  116,83  10 6 м 4
Примечание: аналогичный результат можно получить с уголком меньших или
больших размеров, подобрав соответствующий размер a.
Диаграмма распределения нормальных напряжений по высоте сечения.
МИ
116,25  10 3
2
 МАХ   1 
 y1 

16

10
 159,2 МПа .
JZ
116,83  10 6
МИ
116,25  10 3
2 
 y2 
 9  10  2  89,5 МПа .

6
JZ
116,83  10
Диаграмма распределения касательных напряжений по высоте сечения.
Т  2 В  t   a 2  b  t / 2 35  10 3  2  11  0,8  9  7  0,4   10 6
2 

 0,374 МПа.
6
2
J Z  2B
116,83  10  2  11  10
Т  2 В  t   a 2  b  t / 2 35 10 3  2 11  0,8  9  7  0,4  10 6
3 

 5,14 МПа. .
J Z  2t
116,83 10 6  2  0,8 10  2
Т  2  A  a 2  b  y c  35 10 3  2 13,9 10 4  9  7  1,64  10 2

 7,47 МПа. .
6
2
J Z  2t
116,83 10  2  0,8 10
5. Определение вертикального перемещения концевого сечения стержня.
2 
Универсальное уравнение изогнутой линии включает "начальные параметры" и
слагаемые от нагрузки (составляющие выражение изгибающего момента после
двойного интегрирования):
19
EJ Z  v  EJ Z  v 0  EJ Z   0   M i
x  a M 2
i
  Pi
x  a P 3
i
  qi
x  a q 4
i
2!
3!
4!
i
i
v 0 - перемещение сечения (прогиб) в начале координат,
Здесь:
 0 - поворот сечения в начале координат,
a M i , a Pi , a qi - координаты приложения сосредоточенных моментов M i , сосреi
доточенных сил Pi , начала равномерно распределённых нагрузок q i .
Примечание:
1. Начало координат принимается на одном из концов стержня
2. Распределённая нагрузка, если она не доходит до конца стержня, продлевается и одновременно компенсируется.
3. В уравнении слагаемые от нагрузки, включая и компенсирующие распределённые нагрузки, записываются последовательно при перемещении от принятого начала координат к концу стержня.
Начальные параметры необходимо определять из граничных условий
(ограничений на перемещения в опорных устройствах).
Если начало координат в защемлении, начальные параметры:
v0  v A  0 ,  0   А  0 .
С этими параметрами уравнение 1-го участка: 0  x  a ,
x2
x3
x4
EJ Z  v   M A
 R A   q1 ,
2
6
24
уравнение 2-го участка:
a  x  a  b,
x  a
x  a
x2
x3
x4
EJ Z  v   M A
 RA
 q1
 q1
 q2
,
2
6
24
24
24
4
уравнение 3-го участка:
4
a  b  x  a  b  c,
 x   a  b 
x  a
x  a
x2
x3
x4
EJ Z  v   M A
 R A  q1  q1
 q2
P
2
6
24
24
24
6
4
.
4
Можно заметить, что уравнение каждого следующего участка включает в
3
20
себя предыдущие уравнения, поэтому обычно записывается только последнее
уравнение, в котором уравнения всех других участков отмечаются разделителями с указанием диапазона изменения текущей координаты:
3
4
4
4
x2
x3




x

a

b




x

a
x

a
x
EJ Z  v   M A
 R A  q1  q1
P

q 2
2
6
24
6
24
24
0 x  a
M 
 x   a  b  c 2
2
a  x  a b
 q2
a b x  a b  c
 x abc 4
24
a b  c  x  a b  c  0 , 5 a
При q1  q 2 и х  х В  a  b  c  0,5a  1,5  2  3  0,5  1,5  7,25 м из уравнения находим перемещение свободного конца стержня v B .
7 ,25 2
7 ,25 3
7 ,25 4
EJ Z  v B  116 ,25
 20
 10

2
6
24
5,75 4
3,75 3
0,75 2
0,75 4
 20
 15
 20
 10
 1418 ,36 kH  м 3
24
6
2
24
3
1418,36  10
vB  
 5,781  10  2 м  5,78 см .
11
6
2,1  10  116,83  10
Аналогичным образом, можно определить перемещения и других сечений
стержня и построить график представляющий изогнутую ось стержня.
6. Определение силы, которую необходимо приложить на свободном конце,
чтобы его перемещение отсутствовало.
Из решения задачи
изгиба консольного стержня
сосредоточенной силой
приложенной на свободном
конце перемещение его
равно:
(v B ) X
X  L3
.

3  EJ Z
На основании принципа независимости действия сил перемещения при одновременном приложении нагрузки и силы X определяется алгебраической
21
суммой перемещений от нагрузки и силы, действующих независимо друг от
друга. Из условия, что перемещение концевого сечения должно отсутствовать,
следует равенство перемещений:
X  a  b  c  0,5a 3
(v B ) X 
 vB .
3  EJ Z
Из него находим силу:
Х
v B  3EJ
a  b  c  0,5a 3

5,781  10 2  3  2,1  1011  116,83  10 6
7,25 3
 11,166 кН .
Далее определяются обычным образом реакции в защемлении R *A , M *A ,
строятся диаграммы внутренних сил T , M И и по диаграмме изгибающих моментов изображается искривлённая ось стержня.
Решение проверяется по ранее записанному уравнению изогнутой оси.
Следует убедится, что перемещение концевого сечения стержня с найденной
22
силой действительно отсутствует. Для этого в уравнении необходимо заменить
М А на М *А , R A на R *A :
EJ Z  v B  35,27
7,25 2
7,25 3
7,25 4
 8,83
 10

2
6
24
5,75 4
3,75 3
0,75 2
0,75 4
 15
 20
 10
 1843,56  1843,99  0,43 kH  м 3
24
6
2
24
3
0,43  10
6
B 

17
,
5

10
м  0,0175 мм. (должно быть 0)
2,1  1011  116,83  10 6
0,43
Погрешность расчёта составляет
 100  0,023% .
1843
Перемещения других сечений определяются по уравнению изогнутой оси
при соответствующих значениях текущей координаты х . Например, перемещение сечения ( х  a  b  3,5 м ), где приложена сосредоточенная сила Р будет:
3,5 2
3,5 3
3,5 4
2,0 4
EJ Z  v x 3,5 м  35,27 
 8,83 
 10 
 20 
 103,74 kH  м 3
2
6
24
24
3
 103,74 10
 ч 3,5 м 
 0,423 10 2 м. = 0,423см .
11
6
2,110 116 ,83 10
Можно заметить, что приведённое решение соответствует расчёту статически неопределимой балки с защемлёнием одного конца и с шарнирноподвижной опорой на другом.
 20