переходные процессы в цепях постоянного тока

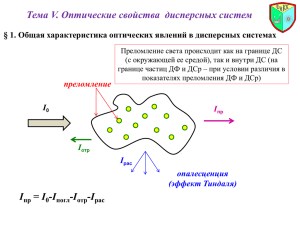
Лабораторная работа №2.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ ПОСТОЯННОГО ТОКА
Цель работы - ознакомление с переходными процессами в простейших цепях
постоянного тока и графическими методами оценки характеристик переходных
процессов.
1. Общие положения
1.1. Постановка задачи
ПЕРЕХОДНЫЕ ПРОЦЕССЫ - это переход системы - электрической цепи – от
одного режима работы к другому, чем-либо отличающемуся от предыдущего:
амплитудой, фазой или частотой входных сигналов тока или напряжения, значениями
параметров схемы или конфигурацией схемы. Переходные процессы вызываются коммутациями - замыканиями или размыканиями выключателей.
Физически переходные процессы - это переход системы от одного
энергетического состояния, соответствующего докоммутационному режиму, к другому послекоммутационному. Если в электрической цепи присутствуют ёмкости или
индуктивности, являющиеся накопителями электрической или магнитной энергии, то
переходной процесс не может происходить скачком, т.к. с энергетических позиций
невозможны скачкообразные изменения энергии и, как следствие напряжения на
конденсаторе и тока в индуктивности. Соответственно, можно сформулировать основные
законы коммутации:
iL (0  )  iL (0  ) ; uC (0  )  uC (0  ) ,
(1.1)
где ” 0  ” и “ 0  ” соответствуют моментам времени до, и после коммутации.
Использование этих законов позволяет однозначно определить состояние электрической
цепи в начале переходного процесса при t  0  .
Математически задача о переходном процессе, вызванном коммутацией,
сводится к отысканию интересующей нас выходной функции xвых (t ) , например,
изменение во времени тока в некоторой ветви схемы или напряжения на некотором
элементе схемы, в результате решения дифференциального уравнения, которое для
линейных цепей с сосредоточенными параметрами R , C , L , M является в общем случае
линейным обыкновенным неоднородным. Решение этого уравнения, xвых (t ) , может быть
получено различными методами, например, классическим, операторным и т.д., и будет
единственным для конкретных начальных условий (см. Приложение 1).
Переходный процесс происходит либо плавно, тогда его называют
апериодическим, либо носит характер затухающих колебаний - его называют
колебательным. В приложении 1 показано, что поведение системы в переходном
состоянии определяется лишь собственными свойствами системы - её конфигурацией и
значениями параметров R , C , L , M .
Для непосредственного наблюдения динамических свойств системы введём
понятие временной или переходной функции системы h(t ) . Если электрическая цепь
подключается к источнику постоянной э.д.с. или постоянного тока величиной x1 или
отключается от источника энергии, то такое воздействие на схему называют ступенчатым
и обозначают xвх (t )  x11(t ) , где 1(t ) - единичная функция. Тогда xвых (t )  x1h(t ) , где h(t ) реакция системы на ступенчатое единичное воздействие.
Временная функция h(t ) достаточно просто может быть получена
экспериментальным путем- подачей на вход системы ступенчатого воздействия xвх (t ) с
одновременным наблюдением выходной величины xвых (t ) , тогда h(t ) будет равна
xв ых (t )
.
x1
Подобный метод называется временным методом исследования динамических свойств
цепи.
В данной работе временным методом исследуются переходные процессы в
простейших неразветвлённых электрических, RC - и RCL - цепях. По виду полученных
кривых hэ (t ) , вообще говоря, можно оценить корни характеристического уравнения и
постоянные интегрирования и записать выражение h р (t ) . Т.к. в исследуемых схемах
известны значения параметров R , C , L , то в результате решения дифференциального
уравнения можно найти hТ (t ) . Согласие зависимостей hТ (t ) и hэ (t ) определяется
погрешностями эксперимента и обработки результатов.
1.2. Переходные процессы в RC - цепях
Если на вход RC - цепи (рис.1.1а) подается ступенчатое напряжение
u1 (t )  u1  1(t ) , то в соответствии с классическим методом решения (см. Приложение 1)
можно найти выражение для выходных функций u 2 (t ) и i (t ) :
u 2 (t )  u пр  u св  u1  Au e pt  u1  u1e
i(t )  iпр  iсв  0  AI e pt 
t

,
u1  t 
e ,
R
(1.2)
u1 (t )
R
u1
t
u1 (t )
i (t )
u 2 (t )
u2 (t )
C
u1
t
i (t )
u1
а)
б)
R
t
Рис.1.1. RC - цепь (а) и временные диаграммы (б),
где значения p находятся из характеристического уравнения 1  RCp  0 : p   1
RC
,
тогда   RC ; постоянные интегрирования определяются по начальным условиям;
независимыми начальными условиями являются uC (0  )  uC (0  )  u 2 (0)  0 . Графики
выходных функций приведены на рис.1.1б. Значение  может быть определено из
графика u 2 (t ) или i (t ) как проекция подкасательной на ось t , проведённой к любой точке
кривой, например, при t  0 .
1.3. Переходные процессы в неразветвлённых RCL - цепях
На рис.1.2. приведена неразветвлённая RCL - цепь. Характеристическое уравнение этой
цепи и выражение для его корней имеют вид:
p2  p
p1, 2  
R
I

 0;
L LC
R
R2
1
1


; p1  p 2 
.
2
LC
2L
LC
4L
Независимые начальные условия:
iL (0  )  iL (0  )  i(0)  0 ; u C (0  )  0 .
(1.3)
(1.4)
R
L
i (t )
u1 (t )
uC
u1 (t )
u1
C
t
uL
u C (t )
u1 (t )
t
u1
t

u C (t )
t
i (t )
t
u L (t )
t
u L (t )
T
 x
t
i (t )
t
Рис.I.2.
В зависимости от соотношения значений R , C , L переходные процессы будут
либо апериодическими, либо колебательными.
Апериодический процесс имеет место, если R  Rкр  2 L
C
. Тогда p1 и p 2 -
отрицательные действительные различные корни и выходные переходные функции,
например, u C (t ) , ищутся в виде:
uC (t )  uСпр  uCсс  u1  A1e p1t  A2 e p2t  u1 
где A1  u1


u1
p2 e p1t  p1e p2t ,
p1  p2
p2
p1
 0 ; A2  u1
 0 ; A1  A2 .
p1  p2
p 2  p1
Выражения для i (t ) и u L (t ) найдём в соответствии с их определением:
i(t )  C


duC
u1

e p1t  e p2t ,
dt
L p1  p2 
(1.5)
u L (t )  L


u1
di

p1e p1t  p2 e p2t .
dt p1  p2
(1.6)
Переходный процесс характеризуется двумя постоянными времени:
1  1 p ,  2  1 p , 1   2 .
1
2
Как следует из выражений (1.5), (1.6) и рис.1.26, определение  1 и  2 путём графической
обработки кривых переходных функций достаточно сложно.
Колебательный процесс (рис.1.2в) будет, если R  Rкр и p1, 2    j , где
1
R2
 2 .
LC 4 L
  R 2L ,  
Динамические характеристики колебательного переходного процесса
следующие:

1


T  2
2L
- постоянная времени затухания,
R
 -период затухающих колебаний.
Переходные функции пишутся в виде:
uC (t )  uCпр  uCсв  u1  Aet sin t  x   u1 
где tgx  
u1
e t sin t  x  ,
 LC
(1.7)
di
u1
duC
u
 1 e t sin( t ) , u L (t )  L  
e t sin( t  x) .
dt
L
dt
 LC
(1.8)
u1
 , A   LC .
Выражения для i (t ) и uL (t ) имеют вид:
i (t )  C
Как следует из графика на рис.1.2в, легко определить величины T и  - как проекцию
подкасательной на ось t , проведённой к огибающей колебаний Ae t в любой точке.
Если R  Rкр , имеет место предельный апериодический процесс, корни будут
равными действительными, т.е. p1  p2  p , и решение ищется в виде:
uC (t )  uCпр  uCсв  uCпр  ( A1  A2t )e pt .
1.4. Схема эксперимента
RC - или RCL - цепь устанавливается переключателем S1 . Переходный процесс
наблюдается на экране осциллографа, для чего обеспечивается его периодическое
повторение с помощью генератора прямоугольных импульсов ГПИ. Частоту повторения
импульсов рекомендуется брать в диапазоне от 25 до 50 Гц.
Подключая щуп осциллографа к различным элементам схемы можно наблюдать
на экране u вх (t ) , u C (t ) , u L (t ) , u R (t ) . Оценка масштаба по оси времени производится по
известной частоте ГПИ, с учётом того, что T  I ,
f
ГПИ
C
uC
L
uL
R
uR
uвх
Рис.1.3. Схема эксперимента.
2. Предварительная подготовка
Внимательно изучить разделы 1.1., 1.2. и Приложение 1. Оформить разделы
отчёта "цели работы", "схемы эксперимента", "теоретические пояснения". В последнем
разделе следует:
1. привести выражения переходных функций u С (t ) , i (t ) для RC - цепи и u C (t ) , u L (t ) ,
i (t ) для RCL - цепи, получающихся при отключении цепей от источника с напряжением
u 0 и замыканием накоротко;
2. провести предварительный расчет значений R , C для RC -цепи и R , C , L для
RCL - цепи, обеспечивающих апериодический и колебательный переходные процессы
таким образом, чтобы длительность переходного процесса t п (см. Приложение 1) не
превышала 0.01с. Допустимые диапазоны изменения: R  0  1 кОм, C  1 40 мкФ,
L  0.02  0.03 Гн. Результаты занести в табл.1.1.;
3. в соответствии с законами коммутации определить n - независимых начальных
условий, т.е. значения токов в индуктивностях и напряжений на конденсаторах для t  0  ,
которые должны быть равны значениям при t  0  ; очевидно, что для этого может
потребоваться расчёт цепи в докоммутационном состоянии;
4. на основе составленной системы из k - уравнений и вычисленных независимых
начальных условиях находится значение i (0) ; для отыскания значений производных
искомой функции при t  0 следует каждый раз (для каждой последующей производной)
целенаправленно образовывать новую систему из k - уравнений путем
дифференцирования одного или нескольких уравнений из системы, используемой на
предыдущем шаге, и сохранения остальных уравнений в неизменном виде;
5. подстановка в систему (3.5) найденных значений i (0) , i   (0) ,  , i ( n1) (0) и
решение её относительно Ai ;
6. окончательная запись решения в виде (3.2) с найденными значениями Ai , p i .
В рассматриваемых в нашем курсе электрических цепях значения p i всегда
отрицательны, если p i - действительные, а если p i - комплексные, то их действительная
часть также отрицательна. В противном случае переходный процесс не будет стремиться к
новому устойчивому состоянию.
Для количественной оценки собственных свойств системы используются
следующие показатели:
p i - действительные отрицательные: постоянные времени системы  i ,
рассчитываемые как  i  1
pi
;  i - это время за которое значение i - ой экспоненты
уменьшается в e раз; геометрически  i равно проекции подкасательной на ось времени t ,
проведённой к любой точке экспоненты (см. рис.3.2а).
Ai e
t
Ae t

t
Ai
t
T
а)
б)
Рис.3.2. Геометрическая интерпретация постоянных времени апериодического
процесса (а) и характеристик колебательного процесса (б).
Переходный процесс в этом случае носит апериодический характер. Т.к. функция
i (t ) стремится к нулю при t   , но никогда не принимает значение " 0 ", то можно
говорить о длительности переходного процесса лишь условно, например, как о времени
t п , когда для всех t > t п выполняется условие
i (t )  iпр (t )  iсв (t ) < i , t > t п .
Обычно за время t п принимается 3 , где  - наибольшая постоянная времени.
p i - комплексные сопряженные, т.е. p1, 2    j ; в этом случае переходной процесс
носит характер затухающих колебаний (см. рис. 3.2б) и представляется периодом
колебаний T  2
1
 и постоянной времени их затухания    .
Таблица 1.1.
Предварительные расчёты значений параметров цепи
Значения
Вид
цепи
Параметров
R, 
C , F
Характер
L, H
tп , s
Rкр
процесса
апериоди-
RC
ческий
RLC
периодический
RLC
колебательный
Следует подготовить кальку и карандаш для срисовывания с экрана осциллографа
переходных процессов.
3. Экспериментальная и расчётная часть
1. Собрать схему эксперимента по рис.1.3.
2. Образовать RC - цепь. Наблюдать на экране осциллографа переходные процессы
при заряде и разряде конденсатора, меняя значения R и C , при этом соблюдать условие
t п < 0.01 с. Срисовать с экрана u вх (t ) , i (t ) , u C (t ) для получения R и C ; рассчитать
 р  RC . Обработать полученные кривые: нанести масштабы по осям, графически
определить значение  э и записать под графиком  э и  р .
3. Образовать RC - цепь. Наблюдать переходные процессы, меняя значения R , C , L .
Установить апериодический режим, записать значения R , C , L и рассчитать  1 и  2 .
Срисовать с экрана u вх (t ) , u C (t ) , u L (t ) , i (t ) . Обработать эти кривые- указать масштабы по
осям, записать для каждого графика и для заряда и для разряда цепи значения
принужденных составляющих и подтвердить, что t п < 0.01 с. Записать под графиками
значения  1 и  2 .
Установить колебательный режим, записать значения R , C , L , рассчитать
значения  и  . Срисовать с экрана входную и выходную функции- u вх (t ) , u C (t ) , u L (t ) ,
u R . Обработать эти кривые- указать масштабы по осям, определить значения Tэ ,  э ,
принуждённые составляющие решений при заряде и разряде. Нанести на графике
значения T р , Tэ и  р ,  э .
4. Анализ результатов
Сопоставить экспериментальные и теоретические результаты и сделать
соответствующие выводы.
5. Перечень контрольных вопросов
1) Как при последовательном соединении R и C значение сопротивления R влияет на
форму кривых тока и напряжения u C ?
2) Объяснить физический смысл постоянной времени и графические методы её
определения.
3) Написать, при каких условиях переходный процесс при последовательном
соединении R , C , L является апериодическим, а при каких условиях имеет
колебательный характер.
4) Нарисовать кривые i (t ) , u C (t ) , u L (t ) при подключении цепи RCL к постоянному
напряжению в апериодическом и колебательном режимах.
ПРИЛОЖЕНИЕ 1
Классический метод расчета переходных процессов.
Постоянные времени системы
Предположим, в некоторой электрической цепи следует определить закон
изменения тока i (t ) в некоторой ветви после коммутации (см. рис.3.1.)
i (t )
П
E
Zн
uн
Рис.3.1.
Поведение системы в переходном процессе в общем случае будет описываться
системой дифференциальных уравнений с k  неизвестными, которые рекомендуется
составлять либо на основе законов Кирхгофа, тогда k  число ветвей цепи, либо по методу
контурных токов, тогда k  число независимых контуров.
Если разрешить эту систему относительно интересующей нас переменной i (t ) , то
получится неоднородное линейное дифференциальное уравнение степени n , где n  число
независимых основных накопителей энергии ( L и C ) в послекоммутационной схеме:
a0
d n i(t )
di (t )
   a n 1
 a n i(t )  b(t ) .
n
dt
dt
(3.1)
В выражении (3.1) коэффициенты a i определяются параметрами цепи R , C , L ,
M и ее конфигурацией, а b(t ) - функция времени, учитывающая действие внешних
источников энергии и, если в послекоммутационной схеме они отсутствуют, то b(t )  0 .
Решение уравнения (3.1) следует искать в виде:
i (t )  iпр (t )  iсв (t ) ,
где iпр (t ) - принуждённый ток, соответствующий частному решению уравнения (3.1) с
правой частью, a iсв (t ) - свободный ток, соответствующий общему решению уравнения
(3.1), когда правая часть равна нулю. В действительности в схеме имеется только ток i (t ) ,
а токи i пр и iсв играют вспомогательную роль- они являются расчётными компонентами,
которым можно приписать определённый физический смысл, облегчающий процедуру их
отыскания, а именно: i пр - значение искомого тока в новом установившемся состоянии
схемы, рассчитываемое любым методом для послекоммутационной схемы;
n
i (t )   Ai e pi t ,
(3.3)
i 1
где p i - корни характеристического уравнения
a 0 p n    a n 1 p  a n  0 ,
(3.4)
Ai -постоянные интегрирования, определяемые из нулевых начальных условий, т.е.
значений искомой функции i (t ) и ее (n  1) производной при t  0 .
Учитывая вышеизложенное, процедура отыскания функции сводится к
следующему:
1. расчёт iпр (t ) по послекоммутационной схеме любым методом.
2. составление характеристического уравнения системы, например, как входное
сопротивление цепи относительно любой ее ветви; отыскание его корней p i и запись
свободной составляющей iсв . Если корни действительные и разные, то
n
iсв (t )   Ai e pi t ;
i 1
если среди n - корней имеются равные действительные корни кратности m , то для них
решение следует записывать в виде:
A  A
i
i 1

t    Ai  m 1t m 1 e pt ;
если среди корней имеются комплексные сопряжённые корни pi ,i 1    j , то для них
решение записывается в виде:
Ai e t sin( t   i 1 ) .
3. составление системы из n - уравнений для отыскания постоянных интегрирования:
i (0)  iпр (0)  iсв (0) ,
 (0)  iсв (0) ,
i (0)  iпр
……………
(3.5)
( n 1)
i ( n1) (0)  iпр
(0)  iсв( n1) (0) .
4. расчёт значений i (0) , i (0) , ……., i ( n1) (0) ; это наиболее трудоёмкая процедура, для
выполнения которой следует:
Составить для послекоммутационной схемы систему из k уравнений на основе
законов Кирхгофа;