подобрать арматуру для балки и проверит её прочность.

ГЛАВА III. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ БАЛОК
1. Общие сведения о железобетонных балках
Балки относятся к изгибаемым элементам, подвергающимся действию
изгибающего момента (М) или изгибающего момента и поперечной силы
(М+Q).
Основные изгибаемые элементы в общей конструкции зданий – плиты и
балки.
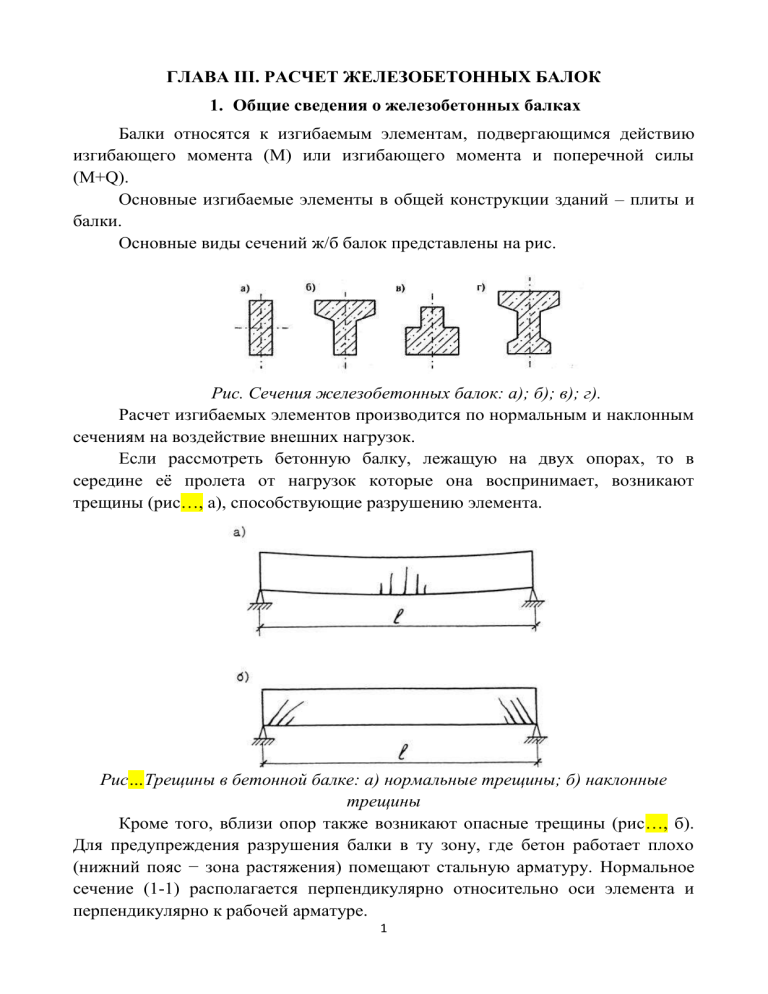
Основные виды сечений ж/б балок представлены на рис.
Рис. Сечения железобетонных балок: а); б); в); г).
Расчет изгибаемых элементов производится по нормальным и наклонным
сечениям на воздействие внешних нагрузок.
Если рассмотреть бетонную балку, лежащую на двух опорах, то в
середине её пролета от нагрузок которые она воспринимает, возникают
трещины (рис…, а), способствующие разрушению элемента.
Рис…Трещины в бетонной балке: а) нормальные трещины; б) наклонные
трещины
Кроме того, вблизи опор также возникают опасные трещины (рис…, б).
Для предупреждения разрушения балки в ту зону, где бетон работает плохо
(нижний пояс − зона растяжения) помещают стальную арматуру. Нормальное
сечение (1-1) располагается перпендикулярно относительно оси элемента и
перпендикулярно к рабочей арматуре.
1
Наклонное сечение (2-2) располагается под углом к оси элемента.
1
2
2
2
2
1
Рис…Появление трещин в бетонном элементе
Для защиты элемента от разрушения по наклонным сечениям его усиляют
специальными арматурными изделиями (отгибы, отдельные стержни, каркасы),
которые
также
как
и
основная
рабочая
арматура
располагаются
перпендикулярно к оси рассматриваемого сечения. Самые опасные участки, на
которых образуются наклонные трещины – участки вблизи опор (≈1/4 длины
балки).
б)
a)
Рис…Виды арматурных элементов для защиты балок от нормальных и
наклонных трещин: а) усиление элемента вертикальными стержнями; б)
усиление элемента отгибами
Разрушение железобетонного элемента начинается тогда, когда в его
наиболее опасных сечениях либо бетон достигает предельных значений либо
арматура приобретает значительные деформации. Разрушение начинается в
сечениях, в которых появляются
максимально предельные
значения
сопротивлений материалов.
Разрушение элемента по наклонному и нормальному сечениям происходит
по различным причинам. По нормальному сечению конструкция разрушается
2
от воздействия изгибающего момента (М), а по наклонному сечению от
воздействия поперечных сил (Q) и реже, изгибающих моментов (М).
В железобетонных «нормально» армированных изгибаемых элементах
разрушение начинается с растянутой зоны, когда расчетные сопротивления
растянутой арматуры достигают своего предела. Возникновение напряжений в
сжатой зоне бетона и разрушение его защитного слоя вызывает разрушение
нижележащих слоёв и постепенное растяжение продольной арматуры.
Увеличение прогиба элемента вызывает растрескивание защитного слоя бетона
в растянутой зоне. Однако, если элемент переармирован, то разрушение может
начаться и со сжатой зоны бетона, при этом напряжения в растянутой арматуре
будут ниже предельных значений, что не удовлетворяет требованиям
оптимального конструирования элементов. Разрушение железобетонного
элемента с жатой зоны может происходить не только из-за некорректного
конструирования. Разрушение бетона сжатой зоны происходит также при
небольших температурах его нагрева и значительных сжимающих напряжениях
в нем, когда пластические свойства бетона при нагреве не успевают проявиться
и модуль упругости снижается незначительно. Этот случай аналогичен
разрушению переармированных железобетонных изгибаемых элементов при
обычной температуре и характеризуется недоиспользованием механических
свойств растянутой арматуры.
Таким образом, различают
две схемы разрушения железобетонных
«нормально» армированных изгибаемых элементов:
1) когда причиной потери прочности элемента будет является достижение в
растянутой арматуре расчетных сопротивлений (Rs) по пределу текучести;
2)когда прочность элемента исчерпывается вследствие разрушения сжатой
зоны бетона раньше чем напряжения в растянутой арматуре достигнут
расчетного сопротивления.
3
Тавровые сечения балок
При расчете прочности нормального сечения изгибаемых элементов
предполагается, что в растянутой зоне бетона образуются трещины, и бетон в
этой зоне уже не работает на восприятие нагрузок. Учитывая то что, что
возникает необходимость оптимизации размеров строительных конструкций и
снижения их материалоемкости, стараются максимально уменьшить расход
материалов (в нашем случае бетона в растянутой зоне), не нарушая при этом
прочности элемента в целом.
В прямоугольном сечении балки можно заметить, что боковые участки
растянутой
зоны
практически
не
участвуют
в
восприятии
нагрузки,
следовательно, их можно убрать. Таким образом, получается тавровое сечение
балки. Такая балка из железобетона работает за счёт того, что сжимающие
усилия
воспринимаются
бетонной
полкой,
а
растягивающие
усилия
воспринимаются достаточным количеством арматуры в ребре элемента.
Рис… Тавровое сечение железобетонной балки: b’f −ширина полки; h’f −
высота полки; b-ширина ребра; h – высота балки; ho − высота рабочей зоны
балки; Аs − площадь сечения растянутой арматуры.
Другим примером такого рода оптимизации формы изгибаемого Ж/б элемента
является видоизменение плит.
4
Рис….Элементы таврового сечения: а) балки таврового и двутаврового
сечения; б)элементы, сечение которых заменяется на тавровое; в)
конструкции, из которых условно вырезается тавровый элемент для
расчета.
При выполнении расчета тавровых элементов встречаются 2 случая их
расчета: 1 случай- когда граница сжатой зоны бетона находится в полке
элемента; 2 случай – когда граница сжатой зоны бетона проходит в ребре
элемента
Рис….Расчетные схемы тавровых элементов при первом и втором расчетном
случае: а) 1-ый случай расчета (х≤h’f); б) 2-ой случай расчета (х>h’f).
5
При расчете балок таврового сечения возникают две основные задачи:
подобрать арматуру для балки и проверит её прочность.
Основные уравнения прочности для нормального сечения тавровых
элементов имеют следующий вид:
Для первого расчетного случая (х≤h’f):
M ≤ Rb·b’f·ho2 ·Ао
M ≤ Rs·Аs· ho·η
Rb·b’f·ho= Rs·Аs
Для второго расчетного случая (х>h’f):
M ≤ Rb·(b’f-b)·h’f (ho-0,5 h’f)+ Rb·b·ho2 ·Ао
Rb∙( b’f-b) ·h’f + Rb·b∙ξ∙ ho = Rs·Аs
Расчетный случай тавровых элементов определяется из предположения,
что нейтральная ось проходит по низу полки, на границе между первым и
вторым случаем.
При этом положение центра тяжести сжатой зоны находится на уровне
половины высоты полки и расстояние между равнодействующей сжимающих
напряжений в бетоне и центром тяжести арматуры определяется как (ho –
0,5h’f), а её величина будет равна Nb=Rb·b’f·h’f
Тогда изгибающий момент, воспринимаемый элементом при полностью
сжатой полке (момент полки) будет равен:
M’f = Rb·b’f·h’f·(ho – 0,5h’f)
Далее сравнивают значения внутреннего момента полки с моментом,
воздействующим на элемент и определяют расчетный случай:
-если М≤М’f то имеет место первый случай расчета тавровых Ж/б элементов;
-если М>М’f то имеет место второй расчетный случай тавровых элементов.
Алгоритм подбора продольной арматуры для Ж/Б балки таврового
сечения:
1.Определяется нагрузка на элемент, строится расчетная схема и определяется
максимальный изгибающий момент.
2.Принимается сечение балки:
6
h≈(1/12-1/8)l, l-длина элемента
b≈(0,3-0,5)h, h-высота элемента
3. задаются классом бетона, классом арматуры и по СНиП определяют их
расчетные сопротивления;
4. Устанавливают коэффициент условий работы бетона (по СНиП).Чаще
всего=0,9
5. Задаются расстоянием от крайнего растянутого волокна бетона до центра
тяжести арматуры(а≈3-5 см)
6. Определяют рабочую высоту балки ho=h-a
7.Определяют расчетный случай тавровых элементов: M’f = Rb·b’f·h’f·(ho –
0,5h’f)
8.В зависимости от расчетного случая имеет место следующие алгоритмы:
Для первого расчетного случая:
8.1. Определяют коэффициент Ao
Ао = M /Rb· γb∙b’f·ho2
8.2. По таблице СНиП определяют коэффициент Aor и сравнивают его с
коэффициентом Ao: Ao ≤ Aor.
Предельные значения коэффициентов Ao и ξ
(при значении коэффициента условий работы бетона 0,9
Класс арматуры
ξr
Aor(Aomax)
А240 (А-I)
0,612
0,425
А300 (А-II)
0,577
0,410
А400 (А-III)
0,53
0,39
Если условие Ao ≤ Aor не выполняется, то изменяют размеры сечения и
материалы балки.
8.3. Через коэффициент Ao определяют значение коэффициента η
8.4. Определяют требуемую площадь арматуры Аs
Аs = M / Rs· ho·η
Для второго расчетного случая:
8.1. Определяют коэффициент Ao
Ао = M -Rb·(b’f-b)·h’f (ho-0,5 h’f)/Rb·γb∙ b·ho2
7
8.2. По таблице СНиП определяют коэффициент Aor и сравнивают его с
коэффициентом Ao: Ao ≤ Aor.
Если условие Ao ≤ Aor не выполняется, то изменяют размеры сечения и
материалы балки.
8.3. По таблице СНиП определяют значение коэффициента 
8.4. Определяют требуемую площадь арматуры
Аs = Rb∙ γb ( b’f-b) ·h’f + Rb ∙γb ·b∙ξ∙ ho /Rs
9. Принимают количество продольных растянутых стержней и определяют
диаметры арматуры и фактическую площадь её сечения.
10.Определяют процент армирования элемента
11. Определяют требуемую площадь монтажных стержней
12. Определяют толщину защитного слоя бетона
14. Конструируют сечение элемента.
Алгоритм определения несущей способности таврового элемента.
1. Определяют расчетные характеристики материалов.
2. Устанавливают коэффициент условий работы бетона γb.
3. По расчетной схеме определяют рабочую высоту сечения, а так же площадь
рабочей продольной арматуры.
4. Определяют значение коэффициента 
Коэффициент  должен быть не больше r , который определяется по СНиП.
Если коэффициент  больше r, то это означает
что элемент
переармирован. В этом случае в дальнейших расчетах принимают значение
r вместо .
5. Определяют высоту сжатой зоны бетона х=· ho и сравнивают высоту полки
с высотой сжатой зоны бетона для определения расчетного случая.
6. По таблице коэффициентов через коэффициент  определяют значение
коэффициента Ao
7. Учитывая случай расчета, определяют величину момента сечения:
Для первого расчетного случая: M сечения = Rb· γb ∙b’f·ho2 ·Ао
8
Для второго расчетного случая: M
сечения
= Ао Rb γb∙ b·ho2 + Rb γb ·( b’f-b)·h’f
(ho-0,5 h’f)
Для проверки прочности элемента необходимо сравнить максимальный
изгибающий момент, действующий на элемент и момент сечения.
Пример
5:
Определить
площадь
поперечного
сечения
арматуры
и
сконструировать балку таврового сечения, если известно: М=150кнм, в
b=300мм,
=500 мм, h=600мм,
=100мм, a=4см, бетон тяжелый В20,
γb=0,9,арматура A-II.
1)Определяем рабочую высоту бетона: ho=h-a=600-40=560мм
2)определяем табличные значения:
Rb=11,5 МПа=11,5·0,9=10,35МПа
Rs=280МПа
3)Устанавливаем случай расчета:
Mf′ = R b ∙ b′f ∙ h′f (ho − 0,5h′f ) = 10,35 ∙ 106 Па ∙ 0,5м ∙ 0,1м(0,56м − 0,5м ∙ 0,1м)
= 263925Нм = 263,9кНм
М=150кНм< М’f=263,9кНм=>имеет место первый случай расчета тавровых
элементов.
4)Проверяем условие Ao ≤ Aor(Aomax)
M
150 ∙ 103 Нм
Ao =
=
= 0,0924
R b ∙ h′f ∙ h2o 10,35 ∙ 106 Па ∙ 0,5м ∙ 0,562
Ao =0,0924< Aor(Aomax)=0,410
5)По таблице коэффициентов определяем значение коэффициента η=0,95
6) Определяют требуемую площадь арматуры:
М
150 ∙ 103 H ∙ м
As =
=
= 0,001007м2 = 1007мм2
η ∙ ho ∙ R s 0,95 ∙ 0,56м ∙ 280 ∙ 106 Па
Принимаем 3Ø22 As,tot=1140мм2
7)Проверяем процент армирования элемента:
μ=
As,tot
1140
∙ 100% =
∙ 100 = 0,63%
b∙h
300 ∙ 600
9
8)Выполняем чертёж-схему армирования.
Задание
5:
Определить
площадь
поперечного
сечения
арматуры
и
сконструировать балку таврового сечения, если известно: М (по варианту), в
b(по варианту),
(по варианту), h(по варианту),
(по варианту), a(по
варианту), бетон тяжелый В(по варианту), γb=0,9,арматура A-II.
№
п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
М, кНм
b,мм
160
300
150
200
320
330
350
250
300
400
500
310
290
150
340
410
150
360
415
160
390
170
180
190
200
200
300
300
200
300
300
300
300
300
200
300
300
300
300
300
300
200
300
300
300
300
300
300
300
300
, мм
500
500
600
500
600
500
600
600
600
600
920
600
920
600
600
920
500
600
920
600
920
600
600
600
600
h,мм
700
600
800
400
800
600
800
800
700
700
400
700
400
800
700
400
400
700
400
800
400
800
800
800
800
10
,мм
70
80
100
60
80
70
100
60
80
100
60
60
70
100
100
80
60
90
90
100
100
100
100
80
80
a,см
4
4
5
4
5
5
5
3
4
3
3
3
4
5
4
5
3
5
5
3
4
4
5
3
5
Бетон
тяжелый
В15
В20
В20
В25
В20
В25
В20
В20
В20
В25
В25
В20
В15
В15
В25
В20
В20
В25
В20
В15
В15
В20
В25
В25
В20