LAB_RAB 1 - Камышинский технологический институт

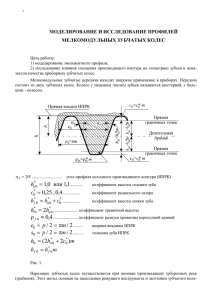
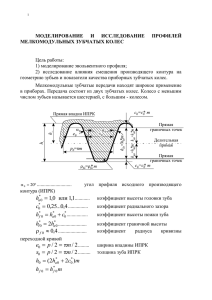
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
УНИВЕРСИТЕТА
КАФЕДРА ОБЩЕТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ
ПОЛУЧЕНИЕ ЭВОЛЬВЕНТНОГО
ПРОФИЛЯ ЗУБА
МЕТОДОМ ОБКАТКИ
Методические указания
к лабораторной работе по дисциплине
«Теория механизмов и машин»
РПК «Политехник»
Волгоград
2002
УДК 621. 831/. 833
П 53
ПОЛУЧЕНИЕ ЭВОЛЬВЕНТНОГО ПРОФИЛЯ ЗУБА МЕТОДОМ
ОБКАТКИ: Методические указания к лабораторной работе по дисциплине «Теория механизмов и машин». / Сост. Е. А. Малявин, А. В. Белов;
Волгоград. гос. техн. ун-т. – Волгоград, 2002. – 10 с.
Излагаются краткие сведения из теории эвольвентного зацепления.
Рассматривается получение эвольвентного профиля методом обкатки, нарезание зубчатых колес со смещением инструмента.
Предназначены в помощь студентам, обучающимся по направлениям
551200 и 552900.
Илл. 3.
Табл. 2.
Библиогр.: 1 назв.
Рецензент Н. Г. Неумоина
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
 Волгоградский
государственный
технический
университет, 2002
2
Цель работы: ознакомиться с нарезанием зубчатых колес с эвольвентным профилем методом обкатки
1.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ
При нарезании зубчатых колес с числом зубьев меньше 17 методом обкатки возникает явление подрезания, которое заключается в том, что головка
зуба инструментальной рейки подрезает эвольвентную часть ножки колеса.
Геометрическим признаком подрезания является то, что рабочая часть линии
зацепления выходит за пределы теоретической её части (рис. 1).
Рис. 1.
На участке Аа не соблюдается основной закон зацепления, профили
инструмента и нарезаемого колеса перестают быть сопряжёнными и целостность эвольвенты нарушается.
Для устранения подрезания прибегают к исправлению профиля. Оно
осуществляется в результате сдвига рейки инструмента относительно
центра заготовки на величину m, которая называется абсолютным сдвигом; m – модуль нарезаемого колеса, мм;  – коэффициент смещения.
Сдвиг инструмента (направление сдвига показано (см. рис. 1) стрелкой)
от центра заготовки называют положительным, к центру – отрицательным.
3
Предельные значения коэффициента смещения исходного контура
ограничиваются следующими факторами:
а) недопустимостью подрезания зубьев;
б) заострением зубьев;
в) уменьшением коэффициента прикрытия.
Значения коэффициентов смещения приводятся в справочной литературе из условий:
а) наибольшей контактной прочности;
б) наибольшей прочности на изгиб;
в) наибольшей износостойкости и сопротивления заеданию.
В данной работе коэффициент смещения  определяется из условия
отсутствия подрезания по формуле:

17  Z
,
17
(1)
где: Z – число зубьев нарезаемого колеса.
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
2.1. Изучение устройства лабораторной установки
Работа проводится на специальном приборе, схема которого представлена на рис. 2.
Рис. 2.
4
На основании прибора установлены диск и рейка. Диск состоит из
2-х частей (верхней и нижней), жёстко связанных между собой и вращающихся, как единое целое, относительно оси, закреплённой в основании
прибора. Диаметр верхнего диска 1 равен диаметру заготовки, а диаметр
нижнего диска 2 равен диаметру делительной окружности колёса d. Рейка
5 со шкалами 8 и 13, планкой 14 и захватами 7 и 16 может перемещаться
поступательно в направляющих 12. Вращение дисков 1 и 2 и поступательное перемещение рейки 5 связаны между собой. В относительном
движении круг 2 (делительная окружность колеса) перекатывается без
скольжения по ребру планки 14 (делительная прямая рейки). Перекатывание осуществляется с помощью следующего устройства. К захватам рейки 7 и 16 прикреплена стальная проволока, огибающая диск 2. Натяжение
проволоки сообщается за счёт некоторого перемещения захвата 7, осуществляемого рукояткой 6. Рейка приводится в движение с помощью шагового храпового механизма. Если нажать на рычаг 10, то рейка перемещается влево на 3 – 4 мм и диск поворачивается на соответствующий
угол. При повороте рычага 11 рейку можно свободно перемещать по
направляющим. Рейка может перемещаться перпендикулярно направляющим, приближаясь к центру заготовки или удаляясь от него. Перемещение рейки отсчитывается по шкалам 8 и 13 и фиксируется винтами 9. На
верхней плоскости рейки указаны основные данные прибора: модуль m,
угол профиля рейки , диаметр делительной окружности d.
2.2. Нарезание нулевого зубчатого колеса (рис. 3) при Х = 0
Наложить на диск 1 (рис. 2) круг из плотной бумаги, закрепить его на
диске крышкой 3 и винтом 4.
Индексы рейки установить против нулевых делений шкал 8 и 13.
Поворотом рычага 11 освободить рейку от храпового механизма и
перевести её в крайнее правое положение.
Последовательно нажимая на рычаг 10, передвигать рейку влево
(каждый раз на один шаг), очерчивая при этом карандашом контур профиля зубьев рейки, до тех пор, пока рейка не переместится влево до упора. На бумаге при этом получится 2 – 3 хорошо очерченных зуба колеса.
5
Рис. 3.
2.3. Нарезание зубчатого колеса со смещением (см. рис. 3)
Вычислить по формуле 1 величину относительного смещения  и абсолютного m сдвига рейки.
Ослабить винты 9, сдвинуть рейку от оси заготовки на величину m,
вновь затянуть винты 9. Повернуть рукоятку 6 влево до отказа. Развернуть диск примерно на 180 относительно рейки, после чего рукоятку
повернуть до отказа вправо. Указанным выше способом вычертить
2–3 зуба колеса со смещением.
6
2.4. Расчёт параметров нулевого и исправленного зубчатого колеса
Определить и занести в отчёт по установленной форме (табл. 1 и 2)
размеры нулевого и исправленного колес.
Характеристики станочного зацепления принять равными: m = 13 мм;
hа* = 1,0;  = 20. Диаметр делительной окружности d = 117 мм. Указать
на макете нарезанных колёс все размеры, относящиеся к геометрии зубчатых колёс и их зубьев, т. е. d; db; da; df; Si; Sb.
ПАРАМЕТРЫ НУЛЕВОГО КОЛЕСА
Наименование
Формула
Z
1. Число зубьев
колеса
Pb  P  сos
4. Толщина зуба
по делительной
окружности, мм.
4.1. Расчётная
4.2. Измеренная
5. Толщина зуба
по основной
окружности, мм.
5.1. Расчетная
5.2. Измеренная
6. Диаметр окружности впадин, мм
7. Диаметр окружности выступов, мм
d
m
P   m
2. Шаг по делительной окружности, мм
3. Шаг по основной
окружности, мм
Таблица 1
Результат
S
m
2
S

S b  d b   inv  
d

d f  d  2m(h *a  c* )  d  2,5m
d a  d  2m  h *a  d  2m
7
S=
Sb =
ПАРАМЕТРЫ ЗУБЧАТОГО КОЛЕСА СО СМЕЩЕНИЕМ
Наименование
Формула
1. Коэффициент
смещения
х
3.1. Расчетная
3.2. Измеренная
4. Толщина зуба по основной окружности, мм
4.1. Расчетная
4.2. Измеренная
5. Диаметр окружности
впадин, мм.
17  Z
17
Х  хm
2. Абсолютный сдвиг
рейки, мм
3. Толщина зуба по делительной окружности, мм
Таблица 2
Результат
S 
m
 2xm  tg
2
 S

Sb  d b   inv  
d

S =
Sb =
d f  d  2m(h *a  c*  x)
Примечание. В таблицах 1 и 2 знаком inv (инволюта ) сокращенно обозначено выражение tg  -  = inv . Указанная функция inv  называется инволютной (эвольвентной) функцией .
Для  = 20 inv  = 0,014904.
2.5. Выводы по работе
Выводы по работе должны содержать ответы на следующие вопросы:
а) какое смещение было проведено (положительное или отрицательное)?
б) как изменились размеры колеса со смещением в сравнении с нулевым?
в) какие достоинства и недостатки выявляются при нарезании зубчатых
колес с положительным и отрицательным смещением исходного контура?
3. СОДЕРЖАНИЕ ОТЧЕТА
1.
2.
3.
4.
Исходные данные.
Образцы нарезанных зубчатых колес.
Расчеты геометрических параметров нарезанных колес.
Выводы по работе.
8
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется эвольвентой и каковы ее основные свойства?
2. Что называется основной, начальной и делительной окружностями?
3. Что такое модуль?
4. Методы нарезания зубчатых колес.
5. В чем суть явления подрезания зубчатых колес?
6. Метод устранения подрезания зубчатых колес при изготовлении
их методом обкатки.
7. Формула для подсчета минимального сдвига рейки, необходимого
для устранения подрезания.
8. Что такое равносмещенное и неравносмещенное зацепление?
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Артоболевский И. И. Теория механизмов и машин: Учебник для
вузов. – 4-е изд., доп. и перераб. – М.: Наука, 1988. – 640 с.
9
Составители: Евгений Александрович Малявин,
Александр Владимирович Белов
ПОЛУЧЕНИЕ ЭВОЛЬВЕНТНОГО ПРОФИЛЯ ЗУБА МЕТОДОМ ОБКАТКИ
Методические указания к лабораторной работе по дисциплине «Теория механизмов и машин»
Редакторы: Попова Л. В., Просондеев М. И.
Темплан 2002г., поз. № 136.
Подписано в печать 03. 07. 2002 г. Формат 1/16.
Бумага потребительская. Усл. печ. л. 0,44.
Уч.-изд. л. 0,63. Тираж 100 экз. Заказ
.
Волгоградский государственный технический университет.
400131 Волгоград, просп. им. В. И. Ленина, 28.
РПК «Политехник»
Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.
ООО «Камипринт»
403850 г. Камышин, Волгоградской обл., ул. Ленина, 20.
10