Document

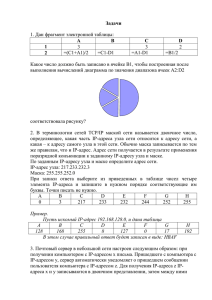
ЕГЭ по информатике
и ИКТ-2013
Часть В
Халиков Ленар Зявдатович, учитель информатики
Муниципальное бюджетное общеобразовательное
учреждение «Шугуровская средняя общеобразовательная
школа имени Валерия Павловича Чкалова»
муниципального образования «Лениногорский
муниципальный район» Республики Татарстан
В1. У исполнителя Арифметик две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 3.
Первая из них увеличивает число на экране на 2, вторая утраивает его.
Например, 21211 – это программа
умножь на 3 прибавь 2 умножь на 3 прибавь 2 прибавь 2,
которая преобразует число 1 в число 19.
Запишите порядок команд в программе преобразования числа 3 в число 69,
содержащей не более 5 команд, указывая лишь номера команд. Если таких
программ более одной, то запишите любую из них.
Решение:
Данную задачу проще решать, если начать с конца.
69:3=23 (2)
23-2=21 (1)
21:3=7 (2)
7-2=5 (1)
5-2=3 (1)
В итоге, команда выглядит так: 11212
Ответ: 11212
В2. Определите значение переменной c после выполнения
следующего фрагмента программы (записанного ниже на разных
языках программирования). Ответ запишите в виде целого числа.
В2. Определите значение переменной c после выполнения
следующего фрагмента программы (записанного ниже на разных
языках программирования). Ответ запишите в виде целого числа.
Решение:
а = 30
b = 14
a = a – 2*b = 30 – 2 * 14 = 30 – 28 = 2
Условие a > b не выполняется, следовательно
с = b – 2 * a = 14 – 2 * 2 = 14 – 4 = 10
Ответ: 10
В3. Дан фрагмент электронной таблицы.
A
B
1
2
4
2
=(B1-A1)/2
=2-A1/2
C
=(C1-A1)*2-4
Какое целое число должно быть записано в ячейке C1, чтобы построенная после
выполнения вычислений диаграмма по значениям диапазона ячеек A2 : С2
соответствовала рисунку? Известно, что все значения диапазона, по которым
построена диаграмма, имеют один и тот же знак.
Решение:
А2 = (B1-A1)/2 = (4-2) / 2 = 1
В2 = 2-A1/2 = 2 – 1 = 1 (это два одинаковых участка)
Следовательно, третий участок в два раза больше одного из них
С3 = (C1-A1)*2 – 4 = 2
(С1 – 2) *2 = 6
С1 – 2 = 3
Ответ: 5
С1 = 5
В4. Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи,
задавая комбинацию точек и тире. Сколько различных символов (цифр, букв,
знаков пунктуации и т. д.) можно закодировать, используя код азбуки Морзе
длиной не менее четырёх и не более пяти сигналов (точек и тире)?
Решение:
Здесь используется бинарный код (точка и тире)
Используя 4 сигнала, можно закодировать 24=16 символа,
используя 5 сигналов, можно закодировать 25=32 символа.
Следовательно, чтоб закодировать символы, используя код азбуки
Морзе длиной не менее четырёх и не более пяти сигналов
необходимо 16 + 32 = 48 символов
Ответ: 48
В5. Определите, что будет напечатано в результате
выполнения программы (записанной ниже на разных языках
программирования).
В5. Определите, что будет напечатано в результате
выполнения программы (записанной ниже на разных языках
программирования).
Решение:
Чтобы выйти из цикла s должно равняться
или быть больше 36.
1) n=n+1=0+1=1
s=s+4=0+4=4
2) n=n+1=1+1=2
s=s+4=4+4=8 и т.д., т.е. получается
число, кратное 4. Число 36 делится на 4:
36/4=9
Ответ: 9
В6. Алгоритм вычисления значения функции F(n), где n – натуральное
число, задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) * n, при n >1
Чему равно значение функции F(5)?
В ответе запишите только натуральное число.
Решение:
F(1) = 1
F(n) = F(n–1) * n, при n >1
F(5) - ?
F(2) = F(2–1) * 2 = 1*2=2
F(3) = F(3–1) * 3 = 2*3=6
F(4) = F(4–1) * 4 = 6*4=24
F(5) = F(5–1) * 5 = 24*5=120
Ответ: 120
В7. Запись десятичного числа в системах счисления с
основаниями 3 и 5 в обоих случаях имеет последней цифрой 0.
Какое минимальное натуральное десятичное число
удовлетворяет этому требованию?
Решение:
Т.к. последнее число 0, то десятичное число должно
одновременно цело делиться на 3 и 5. Минимальное
натуральное число, которое удовлетворяет этому
условию – это 15
Ответ: 15
В8. Ниже на четырёх языках записан алгоритм. Получив на
вход число x, этот алгоритм печатает два числа: a и b.
Укажите наименьшее из таких чисел x, при вводе которых
алгоритм печатает сначала 2, а потом 21.
В8. Ниже на четырёх языках записан алгоритм. Получив на
вход число x, этот алгоритм печатает два числа: a и b.
Укажите наименьшее из таких чисел x, при вводе которых
алгоритм печатает сначала 2, а потом 21.
Решение:
mod – оператор нахождения остатка при
делении двух целых чисел. X mod 10 – при
делении Х на 10 получается самая правая
цифра, младший разряд.
div – оператор нахождения целой части при
делении двух целых чисел. X div 10 – при
делении Х на 10 получается самая левая цифра,
старший разряд.
«a» – должно равняться 2, а «b» – 21.
Значение «а» увеличивается на единицу, т.е. цикл будет выполнятся 2 раза
и каждый раз отбрасываться по одной цифре, поэтому входное значение Х
будет двузначным.
Число 21 можно получить произведением 3 на 7, поэтому при div должно
получиться 3, а при mod – 7.
В8. Ниже на четырёх языках записан алгоритм. Получив на
вход число x, этот алгоритм печатает два числа: a и b.
Укажите наименьшее из таких чисел x, при вводе которых
алгоритм печатает сначала 2, а потом 21.
Решение:
While x>0 a
b
x
-
0
1
37
37>0, True
0+1=1 b=1*(37 mod 10)=7 x=37 div 10=3
3>0, True
1+1=2 b=7*(3 mod 10)=21 x=3 div 10=0
x=0, следовательно, выходим из цикла. Проверяем, a=2, b=21, подходит. В
итоге значения для х будет 37.
Ответ: 37
В9. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л.
По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Л?
Решение:
Рассмотрим все варианты
8. АВЖЛ
1. АБДИЛ
9. АГВДИЛ
2. АБДЖЛ
10. АГВДЖЛ
3. АБВДИЛ
11. АГВЖЛ
4. АБВДЖЛ
12. АГЕЖЛ
5. АБВЖЛ
13. АГЕКЛ
6. АВДИЛ
7. АВДЖЛ
Ответ: 13
В10. Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя
способами.
А. Сжать архиватором, передать архив по каналу связи, распаковать.
Б. Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если:
• средняя скорость передачи данных по каналу связи составляет 220 бит в секунду;
• объём сжатого архиватором документа равен 20% исходного;
• время, требуемое на сжатие документа, – 5 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу
после буквы напишите число, обозначающее, на сколько секунд один способ быстрее
другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно
написать Б23. Единиц измерения «секунд», «сек.», «с.» к ответу добавлять не нужно.
Решение:
Определим время передачи для способа А. Учитываем сжатие
20Мб ∙ 0,2 = 4Мб = 22 Мб = 22 ∙ 210 ∙ 210 ∙ 23 бит = 225 бит
225
220
= 25 = 32с Учитывая время архивации и распаковки, получим: 32+5+1=38с
Определим время для способа Б
20Мб = 20 ∙ 223 бит
20 ∙ 223
= 20 ∙ 23 = 20 ∙ 8 = 160с
20
2
Способ А быстрее: 160 – 38 = 122с
Ответ: А122
В11. В терминологии сетей TCP/IP маской сети называется двоичное число,
определяющее, какая часть IP-адреса узла сети относится к адресу сети, а
какая – к адресу самого узла в этой сети. Обычно маска записывается по тем
же правилам, что и IP-адрес. Адрес сети получается в результате применения
поразрядной конъюнкции к заданному IP-адресу узла и маске.
По заданным IP-адресу узла и маске определите адрес сети.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
При записи ответа выберите из приведённых в таблице чисел четыре
элемента IP-адреса сети и запишите в нужном порядке соответствующие им
буквы, без использования точек.
A
B
C
D
E
F
G
H
0
16
19
64
128
131
192
217
Пример. Пусть искомый IP-адрес: 192.168.128.0, и дана таблица
A
B
C
D
E
F
G
H
128
168
255
8
127
0
17
192
В этом случае правильный ответ будет записан в виде: HBAF
В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
A
B
C
D
E
F
G
H
0
16
19
64
128
131
192
217
Решение:
Преобразуем IP-адрес узла 217.19.128.131 в двоичное восьмиразрядное
представление.
217
2
216 108
1
2
108
54
2
0
54
27
2
0
26
13
2
1
12
6 2
1
6 3 2
19
2
18
9 2
1
8 4 2
1 4 2 2
0 2 1
0 2 1
1
21710 = 110110012 (8 цифр)
0
1910 = 100112 =000100112 (8 цифр)
В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
A
B
C
D
E
F
G
H
0
16
19
64
128
131
192
217
Решение:
Преобразуем IP-адрес узла 217.19.128.131 в двоичное восьмиразрядное
представление.
128
2
128
64
2
0
64
32
2
0
32
16
2
0
16
8 2
0
8 4 2
131
2
130
65
2
1
64
32
2
1
32
16
2
0
16
8 2
0
8 4 2
0 4 2 2
0 4 2 2
0 2 1
0 2 1
0
0
12810 = 100000002 (8 цифр)
13110 =100000112 (8 цифр)
В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
A
B
C
D
E
F
G
H
0
16
19
64
128
131
192
217
Решение:
Получаем вместо 217.19.128.131 следующее значение:
11011001.00010011.10000000.10000011
Преобразуем IP-адрес маски 255.255.192.0 в двоичное восьмиразрядное
представление.
255
2
254 127
1
2
126
63
2
1
62
31
2
1
30
15
2
1
14
7 2
1
6 3 2
1 2 1
192
2
192
96
2
0
96
48
2
0
48
24
2
0
24
12
2
0
12
6 2
0
6 3
2
0 2
1
1
1
25510 = 111111112 (8 цифр)
19210 =110000002 (8 цифр)
В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
A
B
C
D
E
F
G
H
0
16
19
64
128
131
192
217
Решение:
Получаем вместо 217.19.128.131 следующее значение:
11011001.00010011.10000000.10000011
Получаем вместо 255.255.192.0 следующее значение:
11111111.11111111.11000000.00000000
Далее производим поразрядное умножение (конъюнкцию)
1 1 0 1 1 0 0 1. 0 0 0 1 0 0 1 1. 1 0 0 0 0 0 0 0. 1 0 0 0 0 0 1 1 (IP-адрес узла)
1 1 1 1 1 1 1 1. 1 1 1 1 1 1 1 1. 1 1 0 0 0 0 0 0. 0 0 0 0 0 0 0 0 (Маска)
1 1 0 1 1 0 0 1. 0 0 0 1 0 0 1 1. 1 0 0 0 0 0 0 0. 0 0 0 0 0 0 0 0 (IP-адрес сети)
Полученные двоичные числа преобразуем в десятичный код.
7 6 5 4 3 2 1 0
1 1 0 1 1 0 0 12 = 1*27+1*26+0*25+1*24+1*23+0*22+0*21+1*20=128+64+16+8+1=21710
7 6 5 4 3 2 1 0
0 0 0 1 0 0 1 12 = 0*27+0*26+0*25+1*24+0*23+0*22+1*21+1*20=16+2+1=1910
7 6 5 4 3 2 1 0
1 0 0 0 0 0 0 02 = 1*27=12810
0 0 0 0 0 0 0 02 = 010
В итоге получаем, 217.19.128.0 . Это соответствует в таблице HCEA
Ответ: HCEA
В12. В языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого
сегмента сети Интернет.
Запрос
Найдено страниц (в тысячах)
Фрегат | Эсминец
3400
Фрегат & Эсминец
900
Фрегат
2100
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец? Считается,
что все запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
X Y
Z
Необходимо использовать круги Эйлера.
Для Фрегат | Эсминец будет X+Y+Z=3400
Для Фрегат & Эсминец будет Y=900
Для Фрегат будет X+Y=2100
Эсминец
Фрегат
Для Эсминец будет Y+Z=?
Из первого уравнения выражаем Z и вместо (X+Y) подставляем 2100:
Z=3400-(X+Y)=3400-2100=1300
Далее Y+Z=900+1300=2200
Ответ: 2200
В13. У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 2.
Первая из них увеличивает на 1 число на экране, вторая удваивает его.
Программа для Удвоителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 23?
Решение:
Надо использовать древо. Левая ветвь – прибавить 1,
правая ветвь – умножить на 2.
Когда число получится больше 11, дальше правую
ветвь можно и не продолжать, т.к. при умножении
этого числа на 2, мы получим число, превосходящее 23.
Но будет левая ветвь, и она рано или поздно достигнет
числа 23 (по +1).
В13. 1. прибавь 1, 2. умножь на 2.
Сколько есть программ, которые число 3 преобразуют в число 23?
3
4
6
5
8
6
10
7
11
12
9
8
16
10
12
12
14
20
8
14
7
9
18
16
22
11
9
10
20
18
16
10
12
11
22
20
18
12
11
12
22
20
22
Сосчитаем закрашенные круги: 22
Ответ: 22
В14. Определите, какое число будет напечатано в результате выполнения
следующего алгоритма (для Вашего удобства алгоритм представлен на
четырёх языках).
В14. Определите, какое число будет
напечатано в результате выполнения
следующего алгоритма (для Вашего
удобства алгоритм представлен на
четырёх языках).
Решение:
a – левая граница отрезка,
b – правая граница отрезка,
t – счетчик, проходящий отрезок [a;b] с шагом 1,
F(t) – значение функция F в заданной точке,
М – значение, при котором функция F принимает
минимальное значение на оси х (т.к. F(t)<R)
R – текущее минимальное значение функции F.
F = 3*(x-8)*(x-8) = 3*(x-8)2 = 3*(x2-16x+64) = 3x2-48x+192
F – квадратичное уравнение, где a=3, b=-48, c=192
Графиком является парабола, у которой ветви направлены вверх, т.к. а=4 число
положительное.
В14. Определите, какое число будет
напечатано в результате выполнения
следующего алгоритма (для Вашего
удобства алгоритм представлен на
четырёх языках).
Координаты вершин:
−𝑏 48
𝑥0 =
=
=8
2𝑎
6
2
𝑦0 = 3 ∙ 8 − 48 ∙ 8 + 192 = 192 − 384 + 192 = 0
F
Необходимо было определить значение М,
т.е. минимальное значение на оси Х.
Ответ: 8
8
x
В15. Сколько существует различных наборов значений логических переменных
x1, x2, x3, x4, y1, y2 y3, y4, которые удовлетворяют всем перечисленным ниже
условиям?
(x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1
(¬y1 \/ y2) /\ (¬y2 \/ y3) /\ (¬y3 \/ y4) = 1
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) = 1
В ответе не нужно перечислять все различные наборы значений переменных
x1, x2, x3, x4, y1, y2 y3, y4, при которых выполнена данная система равенств. В
качестве ответа Вам нужно указать количество таких наборов.
Решение:
28 = 256 вариантов
Рассмотрим первое условие
(x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1
Если (x1 → x2) = 0, условие выполнятся не будет, т.е. x1=1, x2=0
Если (x2 → x3) = 0, условие выполнятся не будет, т.е. x2=1, x3=0
Если (x3 → x4) = 0, условие выполнятся не будет, т.е. x3=1, x4=0
В15. (x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1
(¬y1 \/ y2) /\ (¬y2 \/ y3) /\ (¬y3 \/ y4) = 1
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Решение:
Построим часть таблицы. В скобках укажем сколько
нулей или единиц будет в столбце
Если (x1 → x2) = 0, условие выполнятся не будет, т.е.
x1=1, x2=0
Если (x2 → x3) = 0, условие выполнятся не будет, т.е.
x2=1, x3=0
Если (x3 → x4) = 0, условие выполнятся не будет, т.е.
x3=1, x4=0
Закрашенные строки не удовлетворяют первому
условию, следовательно 256-16-32-16-64-32-16=80
Остается 80 вариантов
х1
х2
х3
х4
0 (16)
0 (32)
1 (16)
0 (64)
0 (16)
1 (32)
1 (16)
0 (128)
0 (16)
0 (32)
1 (16)
1 (64)
0 (16)
1 (32)
1 (16)
0 (16)
0 (32)
1 (16)
0 (64)
0 (16)
1 (32)
1 (16)
1 (128)
0 (16)
0 (32)
1 (16)
1 (64)
0 (16)
1 (32)
1 (16)
В15. (x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1
(¬y1 \/ y2) /\ (¬y2 \/ y3) /\ (¬y3 \/ y4) = 1
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Решение:
Рассмотрим 2 условие
(¬y1 \/ y2) /\ (¬y2 \/ y3) /\ (¬y3 \/ y4) = 1
Для начала отдельно запишем части не закрашенных строк
по отдельности («внутри» х4)
Если (¬y1 \/ y2) = 0, условие выполнятся не будет, т.е.
у1=1, у2=0
Если (¬y2 \/ y3) = 0, условие выполнятся не будет, т.е.
у2=1, у3=0
Если (¬y3 \/ y4) = 0, условие выполнятся не будет, т.е.
у3=1, у4=0
В итоге еще 11 строк не удовлетворяют условию
Остается 80-11=69 вариантов
Остальные 4 не закрашенные строки из х4 аналогичны,
следовательно
Остается 69-11-11-11-11=25 вариантов
у1
у2
у3
у4
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
В15. (y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Решение:
Рассмотрим 3 условие
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Будем использовать часть таблицы (для удобства
закрашенные участки сохраним)
Если (y1 → x1)=0, условие выполнятся не будет, т.е.
у1=1, x1=0
Пятую не закрашенную строку из х4 рассматривать
не будем, т.к. там x1=1
Здесь есть один вариант, при котором у1=1, x1=0
Остается 25-1=24 варианта
Аналогично из второй, третьей и четвертой не
закрашенной строки х4
Остается 24-1-1-1=21 варианта
Если (y2 → x2)=0, условие выполнятся не будет, т.е.
у2=1, x2=0
Четвертую и пятую не закрашенную строку из х4
рассматривать не будем, т.к. там x2=1
Здесь есть один вариант, при котором у2=1, x2=0
Остается 21-1=20 варианта
Аналогично из второй и третьей не закрашенной
строки х4
Остается 20-1-1=18 вариантов
х1
х2
х3
х4 у1 у2 у3 у4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
1
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
1
0
0
0
0
1
1
1
0
0
0
0
0
1
1
1
1
В15. (y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Решение:
Рассмотрим 3 условие
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Будем использовать часть таблицы (для удобства
закрашенные участки сохраним)
Если (y3 → x3)=0, условие выполнятся не будет, т.е.
у3=1, x3=0
Третью, четвертую и пятую не закрашенную строку
из х4 рассматривать не будем, т.к. там x3=1
Здесь есть один вариант, при котором у3=1, x3=0
Остается 18-1=17 вариантов
Аналогично из второй не закрашенной строки х4
Остается 17-1=16 вариантов
Если (y4 → x4)=0, условие выполнятся не будет, т.е.
у4=1, x4=0
Вторую, третью, четвертую и пятую не
закрашенную строку из х4 рассматривать не будем,
т.к. там x4=1
Здесь есть один вариант, при котором у4=1, x4=0
Остается 16-1=15 вариантов
Ответ: 15
х1
х2
х3
х4 у1 у2 у3 у4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
1
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
1
0
0
0
0
1
1
1
0
0
0
0
0
1
1
1
1