Черкасова Е.В

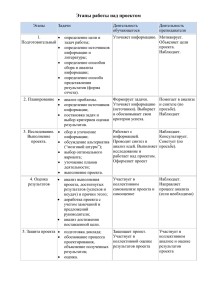
ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ
НА УРОКАХ МАТЕМАТИКИ
КЛАССИФИКАЦИЯ ПРОЕКТОВ
ПО ДОМИНИРУЮЩЕЙ ДЕЯТЕЛЬНОСТИ
УЧАЩИХСЯ
•
•
•
•
•
•
Практико-ориентированный проект
Исследовательский проект по
Информационный проект
Творческий проект
Ролевой проект
Прикладной проект.
• Сбор
информации
• Структурирование
Презентация
• Постановка цели
• Выдвижение
гипотез
• Планирование
результата
Информация
Основная часть
ПРОЕКТ
• Выбор формы
презентации
• Подготовка
презентации
• Презентация
деятельности
В РЕЗУЛЬТАТЕ ФОРМИРУЮТСЯ У ДЕТЕЙ:
• рефлексивные умения (осмысление задачи)
• поисковые умения
• навыки оценочной самостоятельности
• умения и навыки работы в сотрудничестве
• менеджерские умения и навыки
• коммуникативные и презентационные умения и
навыки
ПРЕИМУЩЕСТВА ПЕРСОНАЛЬНЫХ ПРОЕКТОВ:
• план работы над проектом может быть выстроен и отслежен с
максимальной четкостью
• у учащихся максимально формируется чувство ответственности,
поскольку выполнение проекта зависит только от него самого
• учащийся приобретает опыт деятельности на всех без
исключения этапах выполнения проекта – от рождения замысла
до итоговой рефлексии
• формирование у учащихся важнейших общеучебных умений и
навыков (исследовательских, презентационных, оценочных)
оказывается вполне управляемым процессом.
ПРЕИМУЩЕСТВА ГРУППОВЫХ ПРОЕКТОВ:
• у участников проектной группы формируются навыки
сотрудничества
• проект может быть выполнен наиболее глубоко и разносторонне
• каждый этап работы над проектом имеет своего ситуативного
лидера, и наоборот, каждый учащийся, в зависимости от своих
сильных сторон, наиболее активно включен в определенный этап
работы
• в рамках проектной группы могут быть образованы подгруппы,
предлагающие различные пути решения проблемы, идеи,
гипотезы, точки зрения; этот соревновательный элемент, как
правило, повышает мотивацию участников и положительно
влияет на качество выполнения проекта
Накубов Ахрор
Васильева
Деревягина Анна
Екатерина
ЧТО ТАКОЕ ТАНГРАМ?
•
Танграм - это, пожалуй, самая популярная игра из серии так называемых
"геометрических конструкторов". Относительно нее существует следующее
предание.
•
Это было очень давно, почти две с половиной тысячи лет тому назад. У
немолодого императора Китая родился долгожданный сын и наследник. Шли годы.
Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого
императора: его сын, будущий властелин огромной страны, не хотел учиться.
Мальчику доставляло большее удовольствие целый день забавляться игрушками.
•
Император призвал к себе трех мудрецов, один из которых был известен как
математик, другой прославился как художник, а третий был знаменитым
философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы
начала математики, научился смотреть на окружающий мир пристальными глазами
художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую
сложные вещи состоят из простых вещей. И три мудреца придумали эту игру.
МАГИЧЕСКИЙ КВАДРАТ ЯН ХУЭЯ (КИТАЙ).
• В XIII веке математик Ян Хуэй занялся
проблемой методов построения магических
квадратов. Его исследования были, потом
продолжены другими китайскими
математиками. Ян Хуэй рассматривал
магические квадраты не только третьего,
но и больших порядков. Некоторые из его
квадратов были достаточно сложны,
однако он всегда давал правила для их
построения. Он сумел построить
магический квадрат шестого порядка.
ФИГУРЫ ЛИССАЖУ
• Данный вид линий открыл французский
физик XIX века Жюль Антуан Лиссажу
(1822-1880). Он получал их при помощи
точки, совершающей одновременно два
гармонических колебания в двух взаимно
перпендикулярных направлениях.
• Мы рассматриваем ФЛ как движение по
окружности с введением угловых
коэффициентов по формулам:
x = x0 + cos(t / kx) * r
y = y0 - sin(t / ky) * r
kx
ky
1
2
3
4
5
1
2
3
4
5
ФИГУРЫ ЛИССАЖУ
Рассматривая ФЛ, мы задались вопросом, можно ли данные линии задать
уравнениями. Нам удалось вывести такие уравнения для некоторых ФЛ,
коэффициенты которых взаимно просты:
•
kx=1; ky=1: 𝒙𝟐 + 𝒚𝟐 = 𝟏
•
kx=1; ky=2: 𝒙 + 𝟐𝒚𝟐 = 𝟏
•
kx=1; ky=3: 𝒙𝟐 + 𝒚𝟐 𝟒𝒚𝟐 − 𝟑
•
kx=1; ky=4: 𝒙 − 𝟖𝒚𝟐 𝒚𝟐 − 𝟏 = 𝟏
•
kx=1; ky=5: 𝒙𝟐 − 𝟖𝒚 𝟑𝟐𝒚𝟕 − 𝟏𝟔𝒚𝟓 − 𝟑𝟐𝒚𝟒 + 𝟔𝒚𝟑 + 𝟖𝒚𝟐 + 𝟕𝒚 − 𝟐 = 𝟏
•
kx=2; ky=1: 𝟒𝒙𝟐 𝟏 − 𝒙𝟐 + 𝒚𝟐 = 𝟎
•
kx=3; ky=1: 𝒙𝟐 𝟒𝒙𝟐 − 𝟑
•
kx=3; ky=2: 𝒙 𝟒𝒙𝟐 − 𝟑 + 𝟐𝒚𝟐 = 𝟏
•
kx=4; ky=1: 𝟏𝟔𝒙𝟐 𝟒𝒙𝟔 − 𝟖𝒙𝟒 + 𝟓𝒙𝟐 − 𝟏 + 𝒚𝟐 = 𝟎
•
kx=5; ky=1: 𝟔𝟒𝒙𝟒 𝟒𝒙𝟔 − 𝟖𝒙𝟒 + 𝟓𝒙𝟐 − 𝟏 + 𝒚𝟐 = 𝟎
𝟐
𝟐
=𝟏
+ 𝒚𝟐 = 𝟏
ФИГУРЫ КЭРРОЛЛА
• Льюис Кэрролл (настоящее имя Чарльз Лютвидж
Доджсон, 1832-1898) - английский писатель,
математик. По описанию Кэрролла, задавался
бильярдный стол прямоугольной формы,
состоящий длиной kx и шириной ky (kx и ky
натуральные числа). Под ФК мы подразумеваем
траекторию движения бильярдного шара.
Предполагается, что шар движется из левой
верхней вершины под углом 45° и при
столкновении с бортом отражается под тем же
углом. Поскольку, длина и ширина прямоугольника
выражаются целыми числами, рано, или поздно,
шар должен попасть в одну из трёх других угловых
лунок (неугловых нет). Для удобства сравнения мы
задаем движение не по диагоналям квадратов, как
это делал Кэрролл, а по диагоналям
прямоугольников c размерами a/kx и a/ky, на
которые делится квадрат со стороной a.
Классическое представление
ФК с коэффициентами 5, 2
kx
ky
1
2
3
4
5
1
2
3
4
5
ФИГУРЫ КЭРРОЛЛА
Как и в случае с ФЛ, нам стало интересно, можно ли выразить данные фигуры через
уравнения. Потратив немало времени, мы вывели общую формулу для ФК:
𝑦𝑘𝑦 = − 𝑖𝑛𝑡 𝑥 + 2𝑖 𝑚𝑜𝑑2𝑘𝑦 + 𝑥 − 𝑖𝑛𝑡 𝑥
− 𝑘 𝑦 + 𝑘𝑦
В данной формуле не фигурирует коэффициент kx, но он накладывает ограничение на x, т.е.
Параметр i означает то, что данная формула является не
𝑥𝜖 0; 𝑘𝑥
одним уравнением, а семейством подобных уравнений, в
которых i принимает значения от 0 до ky -1.
Также данную формулу можно расписать как систему ky
уравнений, в которой каждое уравнение задает линию,
представленную на рисунке, которая сдвигается и
масштабируется в зависимости от ky.
𝑦1 = − 𝑖𝑛𝑡 𝑥 𝑚𝑜𝑑2𝑘𝑦 + 𝑥 − 𝑖𝑛𝑡 𝑥
− 𝑘 𝑦 + 𝑘𝑦 ,
𝑦2 = − 𝑖𝑛𝑡 𝑥 + 2 𝑚𝑜𝑑2𝑘𝑦 + 𝑥 − 𝑖𝑛𝑡 𝑥
− 𝑘𝑦 + 𝑘𝑦 ,
𝑦3 = − 𝑖𝑛𝑡 𝑥 + 4 𝑚𝑜𝑑2𝑘𝑦 + 𝑥 − 𝑖𝑛𝑡 𝑥
…
− 𝑘𝑦 + 𝑘𝑦 ,
𝑦𝑘𝑦 = − 𝑖𝑛𝑡 𝑥 + 2 𝑘𝑦 − 1
𝑚𝑜𝑑2𝑘𝑦 + 𝑥 − 𝑖𝑛𝑡 𝑥
− 𝑘𝑦 + 𝑘𝑦
ОТКУДА БЕРУТСЯ ПРОБКИ НА ДОРОГАХ?
Попробуем в этом разобраться…
 Невозможность проведения
натурального эксперимента
 Создание математической модели
 Проведение математического
эксперимента
МОДЕЛИРУЮЩАЯ КОМПЬЮТЕРНАЯ ПРОГРАММА
(КОМПЬЮТЕРНАЯ МОДЕЛЬ)
В начале работы нами был выбран язык программирования Visual
Basic 6.0 из-за его структурности, совокупности простоты и
быстродействия.
При разработке программы мы придерживались модульного
принципа.
Вообще программная часть работы не представляла особых
сложностей, поскольку имелась подробно описанная математическая
модель.
ЗАКЛЮЧЕНИЕ
Наша работа пока находится на начальной стадии. Что уже
удалось сделать и что ещё предстоит?
• Уже сделано:
Построена математическая модель прямолинейного участка односторонней дороги, правда со
многими слишком большими упрощениями.
Сделан первый вариант моделирующей программы, отражающий многие, хотя и не все
свойства этой модели.
По созданной программе проведены эксперименты, сделаны выводы и построены графики
Этапы
Подготовка
Задачи
Определение темы, целей, исходного
положения. Выбор рабочей группы.
Деятельность учащихся
Уточняют информацию. Обсуждают и
принимают решение по теме.
Определяют свои роли и
комплектуются в соответствии с ними
в малые группы.
Деятельность педагога
Мотивирует учащихся. Объясняет цели
проекта. Наблюдает. При
необходимости помогает проводить
организационную работу.
Планирование
Анализ проблемы. Определение
источников информации. Постановка
задач и выбор критериев оценки
результатов.
Формируют задачи проекта. Уточняют
информацию (источники). Выбирают
и обосновывают свои критерии
успеха.
Помогает в формулировании задач (по
просьбе). В зависимости от сложности
проекта и степени подготовки
слушателей возможна предварительная
разработка заданий, вопросов для
поисковой деятельности.
Принятие
решения
Сбор и уточнение информации.
Обсуждение альтернатив. Выбор
оптимального варианта. Уточнение
планов деятельности.
Работают с информацией. Проводят
синтез и анализ идей. Выполняют
исследование.
Наблюдает, консультирует,
координирует работу групп.
Выполнение
Работа над проектом. Оформление.
Выполняют исследование и работают Наблюдает, консультирует, советует (по
над проектом. Оформляют проект.
просьбе).
Защита проекта
(презентация)
Подготовка доклада, обоснование
процесса проектирования.
Коллективная защита проекта.
Защищают проект (докладывают о
результатах своей работы).
Участвуют в коллективной оценке
результатов проекта.
Участвует в коллективном анализе и
оценке результатов проекта.
Рефлексия
Анализ выполнения проекта,
достигнутых результатов. Анализ
достижения поставленной цели.
Участвуют в коллективном
самоанализе проекта и самооценке.
Оценивает свою деятельность по
педагогическому руководству
деятельностью детей.
РЕЙТИНГОВАЯ ОЦЕНКА УЧЕБНОГО ПРОЕКТА
Оценка этапов
Критерии оценки
Баллы
1
2
3
Оценка работы
Актуальность и новизна предлагаемых решений, сложность
темы
5, 10,
20
Объем разработок и количество предлагаемых решений
5, 10,
20
Практическая ценность
5, 10
Уровень самостоятельности участников
Качество оформления записки, плакатов и др.
Оценка рецензентом проекта
Оценка защиты
10, 20
5,10,15
5, 10
Качество доклада
5, 10,
20
Проявление глубины и широты представлений по
излагаемой теме
Проявление глубины и широты представлений по
данному предмету
Ответы на вопросы преподавателя
Ответы на вопросы учащихся
5, 10,
20
5, 10,
20
5, 10
5, 10
• Метод проектов предусматривает обязательное наличие
проблемы, требующей исследования.
• В основу его положена идея, составляющая суть понятия
«проект», его прагматическая направленность на результат,
который можно получить при решении той или иной
практически или теоретически значимой проблемы.
• Этот результат можно увидеть, осмыслить, применить в
реальной практической деятельности