Путь - scss.sk

SLOVENSKÁ TECHNICKÁ UNIVERZITA BRATISLAVA
MATERIÁLOVOTECHNOLOGICKÁ FAKULTA V TRNAVE
IŽEVSKÁ TECHNICKÁ UNIVERZITA M. T. KALAŠNIKOVA
Využitie sieťovej analýzy v priemyselných podnikoch
Semestrálna práca
Vypracovala: Elena Lavrenteva
Školiteľ: prof. Ing. Peter Sakál, CSc.
СЛОВАЦКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ В БРАТИСЛАВЕ
ФАКУЛЬТЕТ МАТЕРИАЛОВЕДЕНИЯ В ТРНАВЕ
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М. Т.
КАЛАШНИКОВА
Использование сетевого планирования на промышленных предприятиях
Семестральная работа
Выполнила: Елена Лаврентьева
Проверил: проф. Peter Sakal, кандидат наук.
Práca je taktiež súčasťou schváleného projektu KEGA č.
037STU-4/2012 „Implementácia predmetu „Udržateľné
spoločensky zodpovedné podnikanie“ v rámci študijného
programu Priemyselné manažérstvo na druhom stupni štúdia
na MTF STU Trnava.“
Корпоративная социальная ответственность
Сегодня как никогда возрастает актуальность темы корпоративной социальной
ответственности (КСО, Corporate Social Responsibility, CSR).
«Социальная ответственность бизнеса - обязанность бизнесменов принимать
те решения и следовать тем направлениям деятельности, которые желательны
с точки зрения целей и ценностей общества».
Организации должны нести ответственность перед обществом, в котором
функционируют, направляя часть своих ресурсов и усилий на социальные
нужды, при этом уделяя внимание таким сферам, как защита окружающей
среды, здравоохранение, защита интересов потребителя и т.п.
Понятие сетевого планирования
Типы сетевых диаграмм
Основные термины сетевого планирования
Методы сетевого планирования
4.1 Диаграмма Ганта
4.2 Циклограмма
4.3 Метод критического пути (МКП)
4.4 Метод оценки и пересмотра планов (PERT)
5 Направления применения сетевого планирования
1.
2.
3.
4.
1. Понятие сетевого планирования
• Сетевое планирование – метод управления, который
основывается на использовании математического аппарата
теории графов и системного подхода для отображения и
алгоритмизации комплексов взаимосвязанных работ, действий
или мероприятий для достижения четко поставленной цели.
• Основная цель сетевого планирования - сокращение до
минимума продолжительности проекта.
• Сетевая диаграмма (сеть, граф сети, PERT-диаграмма) —
графическое отображение работ проекта и зависимостей между
ними.
2. Типы сетевых диаграмм
• 1. "вершина-работа"
Определение
требований
системы
Проектирование
системы
2. "вершина-событие" или "дуги-работы"
Подготовка
чертежей
системного
контроллера
Рассмотрение и
утверждение
системного
контролера
Подготовка
чертежей для
оборудования
контроля
температур
Рассмотрение и
утверждение
оборудования
контроля
температур
Утверждение
проекта
системы
Подготовка
площадки
3. Основные термины сетевого
планирования
• Работа – производственный процесс, требующий затрат времени и
материальных ресурсов и приводящий к достижению определенных
результатов.
• Различают различные типы связей в сетевой модели:
• - начальные работы;
• - конечные работы;
• - последовательные работы;
• - работы (операции) дробления;
• - работы (операции) слияния;
• - параллельные работы.
• Событие — это факт окончания одной или нескольких работ,
необходимых и достаточных для начала следующих работ.
• Путь - это любая последовательность работ в сети, в которой
конечное событие каждой работы этой последовательности
совпадает с начальным событием следующей за ней работы.
• Продолжительность пути определяется суммой
продолжительностей составляющих его работ. Путь, имеющий
максимальную длину, называют критическим.
4. Методы сетевого планирования
• К наиболее распространенным методам вероятностного
сетевого планирования относятся:
• метод оценки и анализа программ (PERT);
• метод графической оценки и анализа программ (GERT)
4.1 Диаграмма Ганта
• горизонтальная линейная диаграмма, на которой задачи проекта
представляются протяженными во времени отрезками,
характеризующимися датами начала и окончания, задержками.
4.2 Циклограмма
Виды циклограмм:
а) равноритмичного потока и б) неритмичного потока.
а)
б)
4.3 Метод критического пути (МКП)
Для расчета календарного графика по МКП требуются следующие входные
данные:
• - набор работ;
• - зависимости между работами;
• - оценки продолжительности каждой работы;
• - календарь рабочего времени проекта (в наиболее общем случае
возможно задание собственного календаря для каждой работы);
• - календари ресурсов;
• - ограничения на сроки начала и окончания отдельных работ или этапов;
• - календарная дата начала проекта.
алгоритм определения критического пути
• Aj - самое раннее возможное время наступления события j,
• Bj - самое позднее возможное время наступления события j,
• Dij - длительность процесса (i, j).
• Начальный шаг. Полагаем A1=0; это указывает на то, что проект
начинается в нулевой момент времени. Основной шаг j. Для узла j
определяем узлы p, q, …, v, непосредственно связанные с узлом j
процессами (p, j), (q, j), …, (v, j), для которых уже вычислены
самые ранние времена наступления соответствующих событий.
Самое раннее время наступления события j вычисляется по
формуле 1.
Aj = max { Ap + Dpj, Aq + Dqj, …, Av + Dvj}
(1)
• Проход назад. В этом проходе вычисления начинаются в
последнем узле n и заканчивается в узле 1.
• Начальный шаг. Полагаем Bn = An; это указывает, что самое
раннее и самое позднее времена для завершения проекта
совпадают.
• Основной шаг j. Для узла j определяем узлы p, q, …, v,
непосредственно связанные с узлом j процессами (j, p), (j, q), …, (j,
v), для которых уже вычислены самые поздние времена
наступления соответствующих событий. Самое позднее время
наступления события j вычисляется по формуле 2.
Bj = min {Bp - Djp, Bq - Djq, …, Bv - Djv}
(2)
Проход назад завершается при вычислении величины B1 для узла 1.
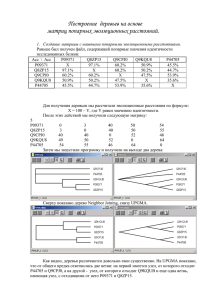
Пример
Найдем критический путь для сети проекта, показанной на рисунке . Длительность
всех процессов дана в днях.
Проход вперед.
• Узел 1. Полагаем A1 = 0.
• Узел 2. A2 = A1 + D12 = 0 + 5 = 5.
• Узел 3. A3 = max { A1 + D13, A2 + D23} = max {0 + 6, 5 + 3} = 8.
• Узел 4. A4 = A2 + D24 = 5 + 8 = 13.
• Узел 5. A5 = max { A3 + D35, A4 + D45} = max {8 + 2, 13 + 0} = 13.
• Узел 6. A6 = max { A3 + D36, A4 + D46, A5 + D56} = max {8 + 11, 13 + 1,
13 + 12} = 25.
Таким образом, расчеты показывают, что проект можно выполнить
за 25 дней.
Проход назад.
• Узел 6. Полагаем A6 = B6 = 25.
• Узел 5. B5 = B6 - D56 = 25 - 12 = 13.
• Узел 4. B4 = min {B6 - D46, B5 - D45} = min {25 - 1, 13 - 0} = 13.
• Узел 3. B3 = min {B6 - D36, B5 - D35} = min {25 - 11, 13 - 2} = 11.
• Узел 2. B2 = min {B4 - D24, B3 - D23} = min {13 - 8, 11 - 3} = 5.
• Узел 1. B1 = min {B3 - D13, B2 - D12} = min {11 - 6, 5 - 5} = 0.
Вычисления без ошибок всегда приводят к результату B = 0.
4.4 Метод оценки и пересмотра планов (PERT)
Метод PERT отличается от СРМ тем, что здесь длительность
процессов характеризуется тремя оценками (А. Таха, 2005):
• 1. Оптимистичная оценка времени а
• 2. Наиболее вероятная оценка времени m
• 3. Пессимистическая оценка времени b,
• На основе этих оценок среднее время 𝐷 выполнения процесса и
дисперсия v вычисляются пo формуле:
• После того как будет вычислено среднее М{ej} и дисперсия var{ej),
вероятность того, что узел j будет достигнут в запланированное
время Sj, можно вычислить по формуле:
где z — случайная величина, имеющая стандартное нормальное
распределение,
Пример
• значения а, m и b, были выбраны так, чтобы 𝐷𝑖𝑗 =𝐷𝑖𝑗 для всех i и j.
Данные представлены в таблице 1
Процесс
i=j
(a, m,b)
Процесс
i=j
(a,m,b)
A
1-2
(3,5,8)
E
3-5
(1,2,3)
B
1-3
(4,6,8)
F
3-6
(9,11,13)
C
2-3
(1,3,5)
H
4-6
(1,1,1)
D
2-4
(5,8,11)
G
5-6
(10,12,14)
• Средние 𝐷𝑖𝑗 и дисперсия Vij для различных процессов даны в
таблице 2. Для фиктивного процесса (а, m, b) = (0, 0, 0), поэтому
его среднее и дисперсия также равны нулю.
Процесс
i-j
Dij
Процесс
Vij
i-j
Dij
Vij
A
1-2
5
0,444
E
3-5
2
0,111
В
1-3
6
0,444
F
3-6
11
0,444
С
2-3
3
0,444
H
4-6
1
0,000
D
2-4
8
1,000
G
5-6
12
0,444
• В таблице 3 приведены самые длинные пути (которые были
определены по средней длительности) от начального узла 1 ко
всем остальным узлам, а также соответствующие средние
значения и дисперсии.
Самый
Среднее
Стандартное
длинный путь
пути
отклонение пути
Узел
2
1-2
5,00
0,67
3
1-2-3
8,00
0,94
4
1-2-4
13,00
1,20
5
1-2-4-5
13,00
1,20
6
1-2-4-5-6
25,00
1,37
• В таблице 4 представлены вычисленные аналитиком значения
вероятностей того, что каждый узел будет, достигнут в
запланированное время Sij .
Самый
Стандартное
Среднее
Узел j
длинный
отклонение
пути
путь
Sj
P(z≤Kj)
Kj
пути
2
1-2
5,00
0,67
5,00
0
0,5000
3
1-2-3
8,00
0,94
11,00
3,19
0,9993
4
1-2-4
13,00
1,20
12,00
-0,83
0,2033
5
1-2-4-5
13,00
1,20
14,00
0,83
0,7967
6
1-2-4-5-6
25,00
1,37
26,00
0,73
0,7673
5. Направления применения сетевого
планирования
Методы сетевого планирования используются при планировании
сложных комплексных проектов:
• Строительство и реконструкция каких-либо объектов;
• Выполнение научно-исследовательских и конструкторских
работ;
• Подготовка производства к выпуску продукции;
• Перевооружение армии;
• Развертывание системы медицинских или профилактических
мероприятий.
сетевая модель позволяет:
• · четко представить структуру комплекса работ, выявить с
любой степенью детализации их этапы и взаимосвязь;
• · составить обоснованный план выполнения комплекса работ,
более эффективно по заданному критерию использовать
ресурсы;
• · проводить многовариантный анализ разных решений с целью
улучшения плана;
• · использовать для обработки больших массивов информации
компьютеры и компьютерные системы.
• Основой органичного развития экономики должно стать
адекватное максимально открытое планирование, задающее
основные параметры для конкретного региона – «ячейки сети».
• Важно помнить о том, что сетевое планирование должно
использоваться только с учетом корпоративной социальной
ответственности и применяться на благо обществу.
Список использованной литературы
• «Operačná analýza» skriptá pre všetky študijné programy Materiálovotechnologickej fakulty STU v Trnave, Ing. Henrieta HrablikChovanová, PhD., prof. Ing. Peter Sakál, CSc., 2010 год
• Гольдин А.К. «Сетевое планирование и управление на предприятиях нефтяной промышленности» 2005. - 112с.
•
Заболотский В.П., Оводенко А.А., Степанов А.Г. Математические модели в управлении: Учеб. пособие/ СПбГУАП. СПб., 2001. 196с
•
Ивасенко А.Г. Управление проектами: учебное пособие/А.Г. Ивасенко, Я.И. Никонова, М.В. Каркавин - Ростов на Дону:
Феникс, 2009. - 330 с. - Высшее образование.
•
Кудрявцев Е.М. Microsoft Project. Методы сетевого планирования и управления проектом. - М.: ДМК Пресс, 2005. - 240 с.
• Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г. Управление проектами: Ученое пособие/ Под общ. ред. И.И. Мазура. - 3-е изд. - М.:
Омега-Л, 2004. - с. 664.
• Таха. А. «Введение в исследование операций: седьмое издание. Издательский дом «Вильямс» Москва ,Санкт-Петербург,
Киев, 2005. - 902с.
• Тынкевич М.А. Экономико-математические методы (исследование операций). Изд. 2, испр. и доп. - Кемерово, 2000. -177 c.
• Управление проектом. Основы проектного управления: ученик/ кол. авт.: под ред. проф. М.Л.Разу. - М.: КНОРУС, 2006. - 768 с.
• http://communitarian.ru/publikacii/gos_stroi/tri_etapa_prezidentskoy_programmy_i_pravitelstvo_natsionalnogo_edinstva/ Мямлин Кирилл, статья «Три этапа президентской программы и правительство национального единства».
СПАСИБО ЗА ВНИМАНИЕ