Тема: Финансовая математика - Все школы Ярковского района

Работу выполнила:
Ученица 10 «А» класса
МАОУ «ЯСОШ»
Каримова Фания
Фаилевна
руководитель:
Ганихина Антонина
Владимировна
Учитель математики
Финансовая математика — раздел прикладной
математики, имеющий дело с математическими
задачами, связанными с финансовыми расчётами. В
финансовой математике любой инструмент
рассматривается с точки зрения генерируемого этим
инструментом некоторого (возможно случайного)
денежного потока.
Я поставила перед собой
следующую цель:
Изучить методы решения
финансовых задач в сфере экономики
с помощью математики.
Для реализации этой цели я поставила следующие
задачи:
1. Изучить вопросы, связанные с различными
долговыми инструментами: векселями, депозитными
сертификатами, облигациями.
2. Провести анализ потоков платежей, применяемый
в банковском деле кредитовании, инвестировании.
3. Провести процентный расчет на базе одного из
банков с. Ярково.
Я планировала разобраться и изучить, как финансовая
математика помогает в кредитовании, исследовав один
из инвестиционных проектов в с. Ярково.
S=P+I
Р – сумма кредита (основная сумма или капитал), I –
доход от инвестированного капитала называется
процентными деньгами или
процентами, Т – период сделки, S – сумма
процентных и основных денег, полагающаяся в
конце периода, называемая итогом или полной
суммой долга.
Отношение процента за период к основной сумме
капиталу) называется нормой процента: r
= I/P.
При заключении конкретных сделок для
обозначения нормы процентов обычно
используется другое название – процентная ставка
(проценты за год) i. Нормированная процентная
ставка представляет собой стоимость единицы
кредитных ресурсов в единицу времени
i = I/PТ или i = r/Т.
Простой процент
Основное уравнение простого
процента: S = P(1 + r) = P(1 + i*T)
Если i - годовая
процентная ставка, то срок сделки Т
измеряется в годах с применением
временных правил.
Будущая сумма долга
В простой кредитной сделке есть два финансовых
события – получение кредита Р в момент t0 и
возврат S в момент t1, т.е. CF = {(t0; Р), (t1; S)}.
Полная сумма долга S по отношению к начальному
моменту есть будущая стоимость долга и
обозначается: S = FVt1(P).
Кредит выдан на 6 месяцев под
10% годовых.
Найти учетные ставки:
1. За период сделки,
2. Формированные – месячную и годовую.
Решение:
w = 0,1*0,5/(1 + 0,1*0,5) = 0, 0476 или 4,76%; dгод =
0,0476 / 0,5 = 0, 0952 или 9,52%
dгод = 0,1 / (1 + 0,1*0,5) = 0,0952 или 9,52%;
dмес = dгод /12 = 0,0952/12 = 0,0079 или 0,79%.
Итог по простой кредитной
сделке:
Описание с помощью процентной ставки полностью
симметрично её описанию исходя из учетной
ставки. Различие состоит в выборе базового
финансового события и актуализации выплаты
процентов. Если базовым событием считать Р, то I
выплачивается в конце, как плата за кредит.
Если базовым событием считать S, то в начальный
момент выплачивается меньшая (дисконтированная)
сумма Р на величину дисконта.
Еще я решила вычислить на базе
Фонда сумму депозитного
сертификата.
Введем термины и обозначения.
Номинал – основная сумма долга F.
Дата эмиссии t0
Дата погашения t1 или срок обращения Т.
r – купонная (нормированная процентная) ставка.
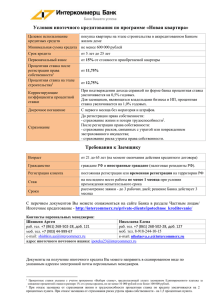
Инвестор покупает по номиналу депозитный
сертификат. Номинал 1000 рублей. Купонная
(нормированная) ставка 20% годовых. Срок
обращения сертификата 270 дней.
Найти сумму погашения сертификата.
Использовать правило АСТ / 365.
Решение.
Для депозитного сертификата купонная ставка с
есть процентная ставка, поэтому S = F(1 + r*T)
S = 1000(1 + 0,2*270 / 365) = 1147,94 (рублей).
 Ответ: 1147,94 рублей.
Пример на базе Фонда:
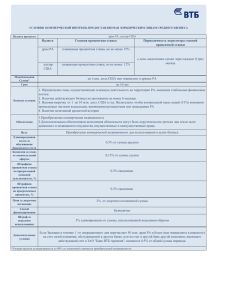
Инвестиционная компания взяла кредит на сумму 1580
000,00, под 7,75% годовых. Я рассчитала помесячно долг
заемщика и составила следующий график:
График возврата займа и начисленных процентов
Сумма займа: 1 580 000 рублей
Срок займа: 36 месяцев
Процентная ставка: 7,75% годовых
Отсрочка первого платежа по возврату основного долга: 2
месяца
№
Дата платежа
Основной долг
(рублей)
Сумма процентов
(рублей)
Всего к оплате
(рублей)
1
2
3
4
5
6
7
8
9
20.12.2010
20.01.2011
20.02.2011
20.03.2011
20.04.2011
20.05.2011
20.06.2011
20.07.2011
20.08.2011
0,00
0,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
4 025,75
10 399,86
10 399,86
9 304,62
9 975,58
9 363,82
9 363,81
8 771,79
8 752,05
4 025,75
10 399,86
56 870,86
55 775,62
56 446,58
55 834,82
55 834,81
55 242,79
55 223,05
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
20.09.2011
20.10.2011
20.11.2011
20.12.2011
20.01.2012
20.02.2012
20.03.2012
20.04.2012
20.05.2012
20.06.2012
20.07.2012
20.08.2012
20.09.2012
20.10.2012
20.11.2012
20.12.2012
20.01.2013
20.02.2013
20.03.2013
20.04.2013
20.05.2013
20.06.2013
20.07.2013
20.08.2013
20.09.2013
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
46 471,00
8 446,17
7 883,75
7 834,41
7 291,72
7 222,65
6 897,87
6 179,54
6 287,78
5 795,77
5 677,69
5 205,36
5 067,60
4 762,55
4 319,75
4 152,46
3 729,34
3 542,37
3 246,19
2 673,91
2 634,43
2 259,48
2 022,67
1 667,46
1 410,91
1 105,03
54 917,17
54 354,75
54 305,41
53 762,72
53 693,65
53 368,87
52 650,54
52 758,78
52 266,77
52 148,69
51 676,36
51 538,60
51 233,55
50 790,75
50 623,46
50 200,34
50 013,37
49 717,19
49 144,91
49 105,43
48 730,48
48 493,67
48 138,46
47 881,91
47 576,03
Из все проделанной работы
можно сделать следующие
выводы, что я:
-изучила методику и практику использования финансовоэкономических расчетов.
-Научилась использовать финансово-экономические расчеты
при решении конкретных задач при отсутствии достоверной
статистической информации, -проводить количественный
анализ финансовых операций,
- строить модели количественных оценок;
- рассчитывать параметры эквивалентного изменения условий
контракта;
-разрабатывать план финансовых операций.
- Иметь представление об управлении финансовой
деятельностью основных институтов рыночной экономики
в условиях неопределенности.
Заключение
В нашей жизни без кредитов и займов не обойтись,
но нужно знать, как все вычисляется. В этом людям
помогает финансовая математика.