Динамика распространения эпидемий
реклама

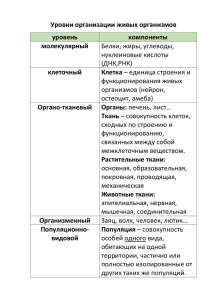
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. М.В.Ломоносова Презентацию подготовила Лопатухина Е.В. Учебная группа №218 Факультет Биологический Москва, 2014г. Крупнейшие эпидемии в истории человечества • Юстинианская чума, 541 г. н. э. • Антонианская чума, 165-180 г.г. • «Черная смерть», XIV-XV века, последующие вспышки вплоть до XVIII в. • Эпидемия ветряной оспы среди коренного населения Америки, 1492-1900 гг. • Первая пандемия холеры, 1817-1823 гг. • Азиатский (российский) грипп, 1889-1890 гг. • Эпидемия сальмонеллеза, 1906 • Грипп «испанка», 1918 - 1919 гг. Современные эпидемии • Малярия • СПИД, 1981 • Грипп • Эпидемии сыпного тифа Страны мира с наиболее высокой степенью распространения ВИЧ/СПИДа среди взрослого населения, 2005 год, доля населения 15-49 лет с выявленным вирусом ВИЧ Чумная палочка при флюоресцентной микроскопии Эритроциты, зараженные P.vivax ВИЧ (зеленый) на поверхности лимфоцита Вирионы оспы Вирус гриппа Сальмонелла Прикладные задачи • Нахождение пороговых значений • Оценка степени тяжести эпидемии • Прогнозирование динамики развитие эпидемии • Моделирование развития ситуации при борьбе с эпидемией Цель данной работы – рассмотреть классическую модель динамики эпидемий Классическая модель Кермака-МакКендрика, 1927г. S I R S – восприимчивые особи I– инфицированные особи R – устраненные особи • Скорость прироста инфицированных особей пропорциональна произведению количества восприимчивых и инфицированных особей • Число восприимчивых особей убывает с такой же скоростью • Скорость перехода инфицированных особей в устраненный класса пропорциональна количеству инфицированных особей • Инкубационный период мал, так что им можно пренебречь, то есть заболевшая особь сразу же переходит в класс инфицированных • Постоянство численности популяции 𝜕𝑆 = −𝑟𝑆𝐼 𝜕𝑡 𝜕𝐼 = 𝑟𝑆𝐼 − 𝑎𝐼 𝜕𝑡 𝜕𝑅 = 𝑎𝐼 𝜕𝑡 S I S(t)+I(t)+R(t)=N или 𝝏𝑺 𝝏𝑰 𝝏𝑹 + + 𝝏𝒕 𝝏𝒕 𝝏𝒕 = 𝟎 − условие постоянства численности, где N – общая численность популяции r>0, скорость инфицирования а>0, скорость убыли инфицированных 1 - время пребывания в инфицированном 𝑎 классе Начальные условия: • S(0)=So>0 • I(0)=Io>0 • R(0)=0 R 𝜕𝑆 𝜕𝑡 ≤ 0 см. модель ⇒ S(t) ≤ 𝑆𝑜 𝑎 𝜕𝐼 𝑆𝑜 < : 𝑟 𝜕𝑡 При эпидемии При 𝑎 𝜕𝐼 𝑆𝑜 > : 𝑟 𝜕𝑡 = 𝐼𝑟(𝑆 𝑎 − 𝑟 ≤ 0 для ∀𝑡 ≥ 0 ⇒ 𝐼𝑜 > 𝐼(𝑡) → нет = 𝐼𝑟(𝑆 𝑎 − 𝑟 ≥ 0 для ∀𝑡 ≥ 0 ⇒ 𝐼𝑜 < 𝐼(𝑡) → эпидемия! Пороговый эффект 𝑎 𝑆𝑜 > ; 𝑟 𝑎 ρ= ; 𝑟 относительная интенсивность устранения 𝑟 σ= 𝑎 интенсивность контактов 𝑟𝑆𝑜 𝑅𝑜 = 𝑎 базовое репродуктивное число количество вторичных заболеваний, появившихся в результате передачи первичного заболевания в популяции, полностью состоящей из восприимчивых особей при 𝑅𝑜 > 1→ эпидемия • Уменьшение 𝑅𝑜 – вакцинация; • «Коллективный иммунитет» – защита всего сообщества, вакцинация чужих детей 𝜕𝐼 𝐼 𝑟𝑆 − 𝑎 𝑟𝑆𝐼 − 𝑎𝐼 𝑎𝐼 − 𝑟𝑆𝐼 𝑎 1 𝜌 =− =− = = −1 + × = −1 + 𝜕𝑆 𝑟𝑆𝐼 𝑟𝑆𝐼 𝑟𝑆𝐼 𝑟 𝑆 𝑆 𝐼≠0 𝜕𝐼 𝜌 = −1 + 𝜕𝑆 𝑆 ⅆ𝐼 = 𝜌 (−1 + ) ⅆ𝑆 𝑆 𝐼 = −𝑆 + 𝜌 ln 𝑆 + 𝒸 𝑰 + 𝑺 − 𝝆 𝒍𝒏 𝑺 = 𝓬 = 𝑰𝒐 + 𝑺𝒐 − 𝝆 𝐥𝐧 𝑺𝒐 Ro = 0 ⇒ 𝐼𝑜 + 𝑆𝑜 = 𝑁 ⇒ при t > 𝟎 𝟎 ≤ 𝑺 + 𝑰 < 𝑵 Imax достигается при S = 𝑎 𝑟 =𝜌 Imax = 𝜌 ln 𝜌 − 𝜌 + 𝐼𝑜 + 𝑆𝑜 − 𝜌 ln 𝑆o= 𝐼𝑜 + 𝑆𝑜 − 𝜌 + 𝜌 ln 𝑆𝑜 =𝑁−𝜌+ 𝜌 ln 𝑆𝑜 𝐼 + 𝑆 − 𝜌 𝑙𝑛 𝑆 = 𝒸 = 𝐼𝑜 + 𝑆𝑜 − 𝜌 ln 𝑆𝑜 𝑎 𝑆𝑜 < 𝑟 нет эпидемии 𝑎 𝑆𝑜 > 𝑟 эпидемия r=2, a=1, N=1 𝜕𝑆 = −𝑟𝑆𝐼 𝜕𝑡 𝜕𝐼 = 𝑟𝑆𝐼 − 𝑎𝐼 𝜕𝑡 𝜕𝑆 𝜕𝑅 = 𝑟𝑆𝐼 − 𝑎𝐼 ⇒ 𝑆 = 𝑆𝑜𝑒 ≥ 𝑆 = 𝑆𝑜𝑒 𝜕𝐼 𝜕𝑡 = 𝐼𝑟(𝑆 − 𝑎 𝑟 ≤ 0 для ∀𝑡 ≥ 0 𝐼 ∞ = 0 ⇒ 𝑅 ∞ = 𝑁 − 𝑆(∞) I = Io + So - 𝑆(∞) 𝐥𝐢𝐦 𝑰 = 𝟎 𝒕→∞ 𝐥𝐢𝐦 𝑺 = 𝑺(∞) 𝒕→∞ = 𝑆 − 𝜌 𝑁 −𝜌 0< 𝑆 ∞ ≤ 𝑁 0< 𝑆 ∞ ≤ 𝜌 Так как 𝜕𝑅 = 𝑎𝐼 𝜕𝑡 = 𝑟 − 𝑆 𝑎 −𝑅(𝑡) 𝜌 Эпидемия угасает из-за уменьшения числа инфицированных особей, а не восприимчивых ≥0 𝜕𝑅 = 𝑎𝐼 𝜕𝑡 𝜕𝑅 𝜕𝑡 𝜕𝑅 𝜕𝑡 = 𝑎𝐼 = 𝑎 𝑁 − 𝑅 − 𝑆 = 𝑎(𝑁 − 𝑅 − 𝑆𝑜𝑒 = 𝑎(𝑁 − 𝑆𝑜 + 𝑆𝑜 𝜌 −1 𝑅− 𝑆𝑜𝑅2 ), 2𝜌2 −𝑅(𝑡) 𝜌 𝑥 ), R(0) = 0; так как 𝑒 = 1 + 𝑥 1! 𝑥2 + 2! + 𝑥3 3! + ⋯ , −∞ < 𝑥 < ∞ (разложение в ряд Тейлора) Гиперболические функции Скорость устранения 𝑑𝑅 𝑑𝑡 = 𝛼= 𝑎𝛼2𝜌2 𝛼𝑎𝑡 2 𝑠𝑒𝑐ℎ 2So 2 𝑟 2 So So 𝜌 −1 2+ − 𝜙 , где 2So(N−So) 𝜌2 𝑎𝛼 2 𝜌2 𝛼𝑎𝑡 2 𝑅 𝑡 = 𝑠𝑒𝑐ℎ −𝜙 2𝑆0 2 , 𝜙 = 𝑡𝑎𝑛ℎ −1 So−1 𝜌 𝛼 Пример. Бомбейская чума 1905-1906 гг. 𝜕𝑅 = 890𝑠𝑒𝑐ℎ2 0,2𝑡 − 3,4 𝜕𝑡 1000 Скорость устранения 900 800 700 600 500 400 300 200 100 0 0 5 10 15 20 Недели 25 30 35 40 Перекрестные инфекции • Шистосоматоз – перекрест между людьми и определенным видом улиток • Бычий туберкулез – перекрест между барсуками и крупным рогатым скотом • Венерические заболевания Яйца Schistosoma sp. Mycobacterium bovis – возбудитель бычьего туберкулеза Гонококк Моделирование венерических заболеваний S I R S I R S I * S I* * R * S * I R* S* I* S, I, R – группы мужчин S*, I*, R* - группы женщин отсутствие иммунитета 𝝏𝑺 = −𝒓𝑺𝑰∗ + 𝒂𝑰 𝝏𝒕 𝝏𝑰 𝝏𝒕 𝑆 𝑡 +𝐼 𝑡 =𝑁 𝑆 ∗ (𝑡) + 𝐼 ∗ (𝑡) = 𝑁 ∗ = 𝒓𝑺𝑰∗ − 𝒂𝑰 𝝏𝑺∗ = −𝒓∗ 𝑰 𝑺∗ + 𝒂∗ 𝑰∗ 𝝏𝒕 𝝏𝑰∗ = 𝒓∗ 𝑺∗ 𝑰 − 𝒂∗ 𝑰∗ 𝝏𝒕 Начальные условия: 𝑆 0 = 𝑆𝑜 I 0 = 𝐼𝑜 𝑆 ∗ 0 = 𝑆𝑜∗ 𝐼 ∗ 0 = 𝐼𝑜∗ Стационарные состояния: 1). I = 0 𝐼∗ = 0 S 𝜕𝐼 = 𝑟𝐼 ∗ 𝑁 − 𝐼 − 𝑎𝐼 𝜕𝑡 2). 𝐼𝑠 = 𝜕𝐼 ∗ = 𝑟 ∗ 𝐼 𝑁 ∗ − 𝐼∗ − 𝑎∗ 𝐼∗ 𝜕𝑡 𝐼𝑠∗ = 𝑁𝑁∗ −𝜌𝜌∗ 𝜌+𝑁 ∗ 𝑁𝑁 ∗ −𝜌𝜌∗ , 𝜌∗ +𝑁 где 𝜌 = 𝑎 ; 𝑟 𝜌∗ = 𝑎∗ 𝑟∗ S* Ненулевые стационарные состояния при 𝑵𝑵∗ > 𝝆𝝆∗ - пороговое условие NN∗ ρρ∗ = 𝑟𝑁 𝑎 × 𝑟 ∗ 𝑁∗ 𝑟𝑁 , где 𝑎∗ 𝑎 − среднее число мужчин, зараженных одной женщиной; для 𝑟 ∗ 𝑁∗ 𝑎∗ аналогично. Линеаризация системы и отыскание характеристических значений 𝑃𝐼′ = −𝑟𝐼 ∗ −𝑎 𝑃𝐼′∗ = 𝑟𝑁 − 𝑟𝐼 Для I= 𝐼 ∗ = 0 −(𝑎+𝑎∗ )± 𝜆1,2 = 𝑄𝐼′ = 𝑟 ∗ 𝑁 ∗ − 𝑟 ∗ 𝐼 ∗ 𝑁𝑁∗ ∗ 2 ∗ (𝑎+𝑎 ) +4𝑎𝑎 𝜌𝜌∗ −1 2 𝑄𝐼′∗ = −𝑟 ∗ 𝐼 − 𝑎∗ Для ненулевых корней 𝜆2 + 𝜆 𝑎 +𝑎∗ +𝑟𝐼𝑠∗ + 𝑟 𝑎𝑟𝐼𝑠∗ + 𝑎𝑟 ∗ 𝐼𝑠 + 𝑟𝑟 ∗ 𝐼∗ 𝑁 + 𝐼𝑁 ∗ + 𝑎𝑎∗ − 𝑟𝑟 ∗ 𝑁𝑁 ∗ = 0 Re𝜆 < 0 ⇒ устойчивый фокус Модель гонореи Четные номера – мужчины Нечетные номера - женщины Активные Неактивные Тяжелая форма N1, N2 (симптомы) Легкая форма N5, N6 (нет симптомов) N3, N4 N7, N8 N1 + N3 + N5 + N7 = 1 N2 + N4 + N6 + N8 = 1 Ii(t), где i=1, 2, …, 8 – доля инфицированных 1-Ii(t) – доля восприимчивых • Di – среднее время (в мес.) инфицирования для группы 𝟏 • - вероятность 𝑫𝒊 излечения за каждый месяц 𝑰𝒊 • - интенсивность Активные Неактивные Тяжелая форма N1, N2 (симптомы) Легкая форма N5, N6 (нет симптомов) устранения в месяц 𝜕 𝑁𝑖 𝐼𝑖 = 𝜕𝑡 𝑗=1 скорость инфицирования 𝑁𝑖 𝐼𝑖 𝐿𝑖𝑗 (1−Ii) 𝑁𝑗 𝐼𝑗 − 𝐷𝑖 заболеваемость N7, N8 𝑳𝒊𝒋 - матрица контактов 8×8; 𝐿𝑖𝑗 = 0 при i + j − четное 𝑫𝒊 8 N3, N4 𝐿𝑖𝑗 (1-Ii) – восприимчивый из группы i заразился от кого-то из j выздоровление Географическое распространение эпидемий • S (x, t) – восприимчивые • I (x, t) – инфицированные 𝝏𝑺 𝝏𝟐𝑺 = −𝒓𝑰𝑺 + 𝑫 𝟐 𝝏𝒕 𝝏𝒙 Безразмерные переменные: 𝐼 ∗ 𝐼 = 𝑆𝑜 𝑆 𝑆 = 𝑆𝑜 ∗ 𝝏𝑰 𝝏𝟐𝑰 = 𝒓𝑰𝑺 − 𝒂𝑰 + 𝑫 𝟐 𝝏𝒕 𝝏𝒙 𝑥∗ 𝑟𝑆𝑜 =𝑥 𝐷 𝑡 ∗ = r𝑆𝑜 𝑡 𝑎 𝜆= 𝑟𝑆𝑜 𝝏𝑺 𝝏𝟐𝑺 = −𝑰𝑺 + 𝟐 𝝏𝒕 𝝏𝒙 𝝏𝑰 𝝏𝟐𝑰 = 𝑰𝑺 − 𝝀𝑰 + 𝟐 𝝏𝒕 𝝏𝒙 𝜆= 𝑎 𝑟𝑆𝑜 1 𝜆 ⇒ - базовое репродукционное число При поиске решений в виде бегущей волны получаем солитон - уединенную волну в средах различной физической природы, сохраняющую неизменной свою форму и скорость при распространении. Заключение Анализирование данных моделей позволяет: • предсказать эволюцию эпидемического процесса • оценить потребность в вакцинации, если вакцина от данного заболевания существует • планировать профилактических и противоэпидемических мероприятий Использованная литература • Дж.Мюррей «Математическая биология», изд. УдГУ, 2011 • Andrew J Black and Alan J McKanе «WKB calculation of an epidemic outbreak distribution». Journal of Statistical Mechanics: Theory and Experiment 10.1088/1742-5468/2011/12/P12006 • С.Л.Плавинский «Моделирование ВИЧ-инфекции и других заразных заболеваний человека и оценка численности групп риска. Введение в математическую эпидемиологию». Москва, 2009