Применение алгоритмов при обучении школьников математике
реклама

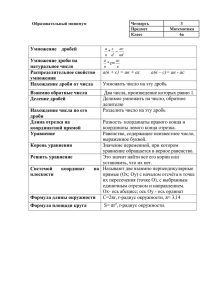
Применение алгоритмов при обучении школьников математике Педагогическая задача: достижение всеми учениками уровня обязательных результатов обучения. Алгоритм точное, общепонятное описание определённой последовательности интеллектуальных операций, необходимых и достаточных для решения любой из задач, принадлежащих некоторому классу. Способы алгоритмизации: • • • • • Формула; Словесное правило; Кластер; Схема; Таблица. Приложение 1 (а - в)2 = а2 - 2ав + в2 1. Указать первое и второе выражение (назвать первое и второе выражение) 2. После знака равенства записать квадрат первого выражения. 3. Вычесть удвоенное произведение первого и второго выражения (можно вначале умножить первое на второе, затем умножить на 2) 4. Прибавить квадрат второго выражения. 5. Каждое слагаемое записать в стандартном (а + в)2 = а2 + 2ав + в2 1. Указать первое и второе выражение (назвать первое и второе выражение) 2. После знака равенства записать квадрат первого выражения. 3. Прибавить удвоенное произведение первого и второго выражения (можно вначале умножить первое на второе, затем умножить на 2) 4. Прибавить квадрат второго выражения. 5. Каждое слагаемое записать в стандартном Составляя алгоритм – программу, необходимо • • • • • • руководствоваться следующими принципами: Теоретический фундамент алгоритма должны составлять теоретические сведенья, имеющие непосредственное отношение к нему. Система предписаний, имея дискретный характер, должна быть общей по отношению к целому классу однородных задач. По содержанию система предписаний должна быть полной или достаточной, т. е. обеспечивать на каждом конкретном шаге учебной деятельности учащихся однозначное получение промежуточной информации, которая в своём комплексе гарантирует получение конечного результата. Система предписаний должна быть совместимой или непротиворечивой, т. е. каждое предыдущее предписание должно являться малой посылкой для последующего, а последующее – логическим следствием предыдущего. Число пунктов программы не должно быть большим. Это обеспечивает его подвижность: объединение отдельных шагов или дробление шагов на более элементарные. Система предписаний должна обеспечивать многократное решение однотипных задач, т. е. обладать свойством массовости. Алгоритм составления уравнения касательной к графику функции. Уравнение касательной Алгоритм нахождения наибольшего и наименьшего значения функций. 1 Выяснить, определена ли и является ли функция y=f(x) непрерывной на указанном отрезке [a;b] или промежутке (a;b) 2 Найти производную функции f/(x) 3 Найти критические точки (точки, в которых f/(x)=0 или f/(x) не существует) 4 Выбрать критические точки принадлежащие [a;b] или (а;b) 5 Если [a;b] Найти значение функции в критических точках (внутри отрезка) и на его концах Если (а;b) Определить вид экстремума в критических точках (внутри интервала) и вычислить его значение 6 Из найденных значений выбрать наибольшее и наименьшее Выбрать наибольшее и наименьшее из минимумов и максимумов функции соответственно 7 Выписать ответ Задания для учащихся 9-х классов по проверке умения планировать свою деятельность Задание №1. Упростите выражение: 2х(х + 4) – (2 – 3х)2. • Выделите действия, которые вы выполняете для решения данной задачи и перечислите их по порядку: • раскрытие скобок; • умножение многочлена на многочлен; • умножение одночленов; • умножение одночлена на многочлен; • приведение подобных слагаемых; • применение формул сокращенного умножения: а) разность квадратов двух выражений; б) квадрат суммы двух выражений; в) квадрат разности двух выражений • запись ответа. Задание №2. Сравните дроби, предварительно записав алгоритм сравнения: а). 0,37 и 0,04; б). 33 и 23 ; в). 8 и 0,88. 102 9 приложение: 1.обе дроби обыкновенные; 2.обе дроби десятичные; 3.одна обыкновенная, другая десятичная; 4.приведение дробей к общему знаменателю; 5.сравнение дробей по разрядам; 6.перевод десятичной дроби в обыкновенную дробь; 7.перевод обыкновенной дроби в десятичную дробь; 8.сравнение числителей дробей с одинаковыми знаменателями. Задание №3. 4 5 5 4 Запишите дроби: 0,67; 0,7; и а). в порядке возрастания; б). в порядке убывания; составьте и запишите алгоритм выполнения задания Приёмы: • Использование стимулирующих звеньев; • Реконструкция; • Мысленное составление плана; • Прогнозирование; • Соотнесение; • Выделение смысловых опорных пунктов;