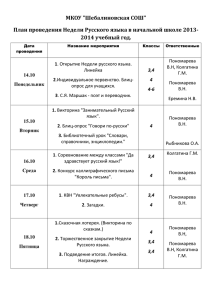
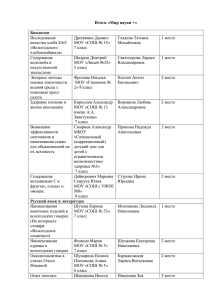
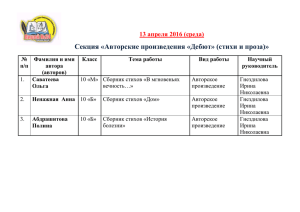
Теория вероятности Задачи для подготовки к ГИА и ЕГЭ

Теория вероятности
Задачи для подготовки
к ГИА и ЕГЭ
Введение
В настоящее время основой описания
научной картины мира стали
вероятностно – статистические законы.
Современная физика, химия, биология,
демография, социология, лингвистика,
весь комплекс социально –
экономических наук развиваются на
вероятностно-статистической базе.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Приказом Минобразования России
"Об утверждении федерального
компонента государственных
стандартов начального общего,
основного общего и среднего (полного)
общего образования" от 5 марта 2004 г.
№ 1089
Элементы теории вероятности и
математической статистики были
введены в программы по математике
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
«элементы логики, комбинаторики,
статистики и теории вероятностей
становятся обязательным
компонентом школьного
образования, усиливающим его
прикладное и практическое
значение».
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Что изучает теория вероятности?
 Закономерности,
возникающие при
многократном повторении
случайных явлений
 Вероятность — числовая
характеристика возможности
появления случайного события в
определенных условиях, которые
могут быть воспроизведены
неограниченное число раз.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Современная Теория вероятности
ушла от азартных игр также далеко, как
геометрия от задач землеустройства, но
их реквизит по-прежнему остается
наиболее простым и надежным
источником случая.
 Поэтому материалом для экспериментов
чаще всего служат монета, кубик,
рулетка, колода карт.

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Понятия
Эксперимент (опыт), результат которого
нельзя точно предсказать до его
осуществления, называют случайным
 Взаимоисключающие друг друга результаты
случайного эксперимента называют исходами
или элементарными событиями, их
совокупность – множеством исходов
эксперимента.
 Любое подмножество множества исходов 
событие
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Событие
невозможное
 случайное
 достоверное

 Бросаем
два кубика.
А={сумма очков на кубиках равна 20}
 B={сумма очков на кубиках равна 11}
 C={на двух кубиках выпало число
очков, больше 1, но меньше 13}

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Что вероятнее?
А={вытянуть пиковую даму из
перетасованной колоды карт}
В = {вытянуть шестерку из
перетасованной колоды карт}
С = {получить шестерку при
подбрасывании кубика}
Шансы
имеет смысл сравнивать как дроби:
1 шанс из 6 лучше, чем 4 шанса из 36
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Математическая модель опыта
 Построение
математической модели
эксперимента предполагает описание:
 Возможных исходов
 Событий
 Вероятности наступления этих
событий
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Множество исходов эксперимента


Ваня два раза
подбрасывает монету
и после каждого
броска записывает на
листе, что выпало –
герб или цифра.
Описать множество
исходов эксперимента.

Маша рисует в тетради
отрезок ОА длиной 10
см, произвольно ставит
на нем точку В, после
чего измеряет длину
отрезка ОВ. Описать
множество исходов
данного эксперимента.
Ω = { ГГ,ГЦ,ЦГ,ЦЦ }  Ω = { х | 0 ≤ х ≤ 10 }
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Множество исходов эксперимента

В коробке лежат три шара: К, С, Б.
Извлекаются два из них и фиксируются их
цвета. Описать множество исходов.
Возвращается шар?
Учитывается порядок?
1
1.Ω
2
Учитывается порядок?
3
4
={ кс,ск,кб,бк,сб,бс }
нд - РБП
2.Ω ={ кс,кб,сб}
нн – СБП
3.Ω ={кс,ск,кб,бк,сб,бс,кк,сс,бб} дд – РП
4.Ω ={кс,кб,сб,кк,сс,бб}
дн - СП
Аксиоматическое определение
вероятности (А.Н. Колмогоров)
 Ω = {ω1, ω2 …ωn } множество всех исходов
эксперимента.
 Р (Ω) – неотрицательная числовая
функция, для которой
 р(ω1)+ р(ω2)+…+ р(ωn)=1 распределение
вероятности на Ω
 Событие А – любое подмножество Ω
 Р(А) – сумма вероятностей входящих в
него исходов
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Как часто происходит событие?
Абсолютная частота – количество
повторений данного события в серии
испытаний
 Относительная частота –доля
экспериментов, завершившаяся
наступлением данного события
 Относительную частоту можно найти,
поделив абсолютную частоту на число
экспериментов

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Статистическое определение
вероятности

За вероятность случайного события
можно приближенно принять его
относительную частоту, полученную в
длинной серии экспериментов.

После десяти бросаний двух кубиков
сумма 12 не была получена ни разу.
Можно ли утверждать, что вероятность
этого события равна нулю?
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Статистическая вероятность
Оценить вероятность того, что диод
способен проработать свыше 10 тыс.
часов
 На стенде испытаний: 1000 диодов
 Через 10 тыс. часов 100 штук «сгорели»


Искомая вероятность ≈ 9/10
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Классическое определение
вероятности

Пусть все исходы равновозможны.
 A — событие из числа равновозможных
случаев
 N – число всех возможных исходов
эксперимента
 M – число исходов, благоприятных для
события А
 Вероятность случайного события А
Р(А) = M : N
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Какова вероятность встретить
белого медведя на улице?
 Ответ:
½ (либо встретишь, либо не
встретишь)
 Где ошибка?
 События не равновозможные
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Ошибка Даламбера
Какова вероятность, что подброшенные
вверх две правильные монеты упадут на
одну и ту же сторону?
 Опыт имеет три равновозможных исхода
 1) Обе монеты упали на «орла»
 2) Обе монеты упали на «решку»
 3) одна из монет упала на «орла»,
другая – на «решку»
 Вероятность равна 2:3 ?

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Геометрическая вероятность
Множество исходов – некоторое
множество точек на числовой прямой,
на плоскости или в пространстве,
имеющее меру (длину, площадь, объем)
 Вероятность попадания в любую часть
множества пропорциональна мере этой
части

 Р(А)
= m(А) : m(Ω)
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Геометрическая вероятность
Выберем на географической карте
Европы случайную точку. Какова
вероятность, что эта точка окажется в
России?
 Для ответа нужно знать, какую часть
площади всей карты составляет
площадь России.
 Отношение этих площадей даст искомую
вероятность.

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Геометрическая вероятность
 На
светофоре одну минуту горит
зеленый свет, две минуты красный,
одну минуту зеленый, две минуты
красный и т.д. В случайный момент
времени к перекрестку подъезжает
автомобиль. Какова вероятность
того, что он проедет перекресток
без остановки?
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи о светофоре
Опыт состоит в случайном выборе
момента t из промежутка от 0 до 3 минут
 Множество исходов Ω = [0;3]
 Событие А={автомобиль проезжает
перекресток без остановки} задается
неравенством 0≤ t ≤ 1

 Р(А)
=1:3
(отношение длин отрезков)
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№1
В
случайном эксперименте
бросают две игральные кости.
Найдите вероятность того, что в
сумме выпадет 8 очков. Результат
округлите до сотых
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №1:




Событие А – «в сумме выпало 8 очков»
Рассмотрим возможные исходы при двух бросках.
Количество вариантов различных чисел, выпавших на
первой кости равно 6. Каждому из них соответствует
любой из 6 вариантов, выпавших на второй кости. Значит,
количество возможных исходов равно 6*6=36
Рассмотрим благоприятные исходы.
Сумма в 8 очков могла получиться при следующих
вариантах двух бросков:
1бросок
2
3
4
5
6
2 бросок
6
5
4
3
2
Количество
благоприятных исходов равно 5
Найдем вероятность события А - Р(А)= 5:36
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№2
В
случайном эксперименте
симметричную монету
бросают дважды. Найдите
вероятность того, что орел
выпадет ровно один раз
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи № 2:

Событие А – «орел выпал ровно один раз»
Рассмотрим возможные исходы после двух
бросков монеты.
1бросок
орел
орел
решка
решка
2 бросок
орел
решка
орел
решка
Количество
возможных исходов равно 4
Количество благоприятных исходов - 2
Найдем вероятность события А:
Р(А)= 2:4 = 0,5
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№3
Миша,
Рома, Олег, Паша
и Дима бросили жребий
– кому начинать игру.
Найдите вероятность
того, что начинать игру
должен будет Рома.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи № 3:






Рассмотрим возможные исходы:
«Игру начинает Миша»
«Игру начинает Рома»
«Игру начинает Олег»
«Игру начинает Паша»
«Игру начинает Дима»
Количество
возможных исходов равно 5
Количество благоприятных исходов - 1
Событие А – «Игру начинает Рома»
Найдем вероятность события А:
 Р(А)= 1:5 = 0,2
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№4

Конкурс исполнителей проводится в 3
дня. Всего заявлено 40 выступлений –
по одному от каждой страны. В
первый день 30 выступлений,
остальные распределены поровну
между оставшимися днями. Порядок
выступлений определяется жребием.
Какова вероятность, что выступление
представителя России состоится в
третий день конкурса?
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи № 4:
Событие А: «Представитель России
выступит в третий день конкурса»
 Всего заявлено 40 выступлений – это
количество всех возможных исходов.
 В третий день состоится
 (40 - 30) : 2 = 5 выступлений – это
количество благоприятных исходов для
события А
 Значит, Р(А) = 5 : 40 = 0,125

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№5
 Игральную
кость (кубик) бросили
один раз. Какова вероятность
того, что выпало менее 4 очков?
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №5:
 Событие
А – «выпало 1, 2 или 3 очка»
 Все возможные исходы:
1, 2, 3, 4, 5, 6
 Благоприятные исходы: 1, 2, 3.
 Вероятность события А:
Р(А) = 3 : 6 = 0,5
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№6

На соревнования по метанию ядра
приехали 2 спортсмена из
Великобритании, 2 из Испании и 4 из
Швейцарии. Порядок выступлений
определяется жребием. Найдите
вероятность того, что восьмым будет
выступать спортсмен из Испании.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №6:
Событие А – «восьмым выступает спортсмен
из Испании»
 Восьмым может выступать с равной
вероятностью любой из восьми спортсменов.
Число всех исходов – 8.
 Число благоприятных исходов – 2
(2 спортсмена из Испании)
Р(А) = 2 : 8 = 0,25

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№7

Перед началом футбольного матча
судья бросает монету, чтобы
определить, какая из команд будет
первая владеть мячом. Команда
«Витязь» по очереди играет с
командами «Атлант» и «Титан».
Найдите вероятность того, что
команда «Витязь» не выиграет право
первой владеть мячом ни в одном
матче.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №7:
Событие С – «команда «Витязь» не
выиграет право первой владеть
мячом ни в одном матче.
 Найдем число всех исходов.
Возможные исходы жеребьевок : ВВ,
АВ, АТ, ВТ
 Благоприятные исходы: АТ
 Вероятность события С:
Р(С) = 1 : 4 = 0,25

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№8
В
сборнике билетов по географии
всего 25 билетов, в 6 из них
встречается вопрос о водоемах.
Найдите вероятность того, что в
случайно выбранном на экзамене
билете школьнику встретится
вопрос о водоемах.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№9
 Люда
дважды бросает
игральный кубик. В сумме у
нее выпало 9 очков. Найдите
вероятность того, что при
первом броске выпало 5
очков.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №9:
Событие С – «Выпало 5 очков при первом
броске».

Найдем число всех исходов.
Возможных исходов 4:
1 бросок
6
5
4
3
2 бросок
3
4
5
6
Число благоприятных исходов – 1.
 Р(С) = 1 : 4 = 0,25

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№10
На чемпионате по прыжкам в воду
выступают 50 спортсменов, среди них
3 прыгуна из России и 5 прыгунов из
США. Порядок выступлений
определяется жребием. Найдите
вероятность того, что сорок вторым
будет выступать прыгун из России.
 Ответ: 0,06

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №10:
Событие С – «сорок вторым будет
выступать прыгун из России»
 Число всех исходов – 50, так как
каждый из 50 спортсменов может
выступать сорок вторым.
 Число благоприятных исходов - 3
 Вероятность события С:
Р(С) = 3 : 50 = 0,06

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№11
В
среднем из 500 фонариков,
поступивших в продажу, 5
неисправны. Найдите
вероятность того, что один
купленный фонарик окажется
исправным.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №11:
Статистическая вероятность.
 На стенде испытаний – 500
фонариков
 Неисправных среди них 5
 Вероятность купить неисправный
фонарик
5 : 500 = 0,01
 Значит, исправный можно купить с
вероятностью 1- 0,01 = 0,99

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№12

Лена и Саша играют в кости. Они
бросают кость по одному разу.
Выигрывает тот, кто выбросил больше
очков. Если очков выпало поровну, то
наступает ничья. В сумме выпало 8
очков. Найдите вероятность того, что
Лена выиграла.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №12:
Событие С – «выпало больше очков при броске
Лены».

Найдем число исходов с суммой очков 8.
Возможных исходов 5:
бросок Лены
6
5
4
3
2
бросок Саши
2
3
4
5
6
Из них благоприятных исходов - 2.
 Р(С) = 2 : 5 = 0,4

Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
№13

В чемпионате мира участвует 15 команд. С
помощью жребия их нужно разделить на
пять групп по три команды в каждой. В
ящике вперемешку лежат карточки с
номерами групп:
1,1,1,2,2,2,3,3,3,4,4,4,5,5,5
Капитаны команд тянут по одной карточке.
Какова вероятность того, что команда
Италии окажется в третьей группе?
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Решение задачи №13:
 Событие
С – «капитан Италии
вытащил карточку с номером 3»
Число всех исходов – 15
Число благоприятных исходов – 3
Вероятность события С:
Р(С) = 3 : 15 = 0,2
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Развитие теории вероятности
 На
первом этапе истории этой
науки она рассматривалась
как собрание курьезных
задач, связанных в первую
очередь с азартными играми
в кости и карты.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
 Первоначально
её основные
понятия не имели строго
математического вида, к ним
можно было относиться как к
некоторым эмпирическим
фактам, как к свойствам
реальных событий и они
формулировались в
наглядных представлениях.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Во второй половине XIX века
основной вклад внесли русские
учёные П. Л. Чебышев, А. А. Марков
и А. М. Ляпунов. Современный вид
теория вероятностей получила
благодаря аксиоматизации,
предложенной А. Н. Колмогоровым.
В результате теория вероятностей
приобрела строгий математический
вид и окончательно стала одним из
разделов математики.
Пономарева Ирина Николаевна, МОУ
гимназия 9 г.Екатеринбурга
Основатели
«Теории вероятности»
Б. Паскаль
Я. Бернулли
Х. Гюйгенс
П. Ферма
Литература:

Мордкович А.Г., Семенов П.В. События.
Вероятность. Статистика: Дополнительные
материалы к курсу алгебры для 7-9 кл. – М.:
Мнемозина, 2002. (к учебникам А.Г.
Мордковича)
 Ткачева М.В., Федорова Н.Е. Алгебра, 7-9:
Элементы статистики и вероятность. - М.:
Просвещение, 2007.
(к учебникам А.Ш. Алимова и др.)
 Бунимович Е.А., Булычев В.А. Вероятность и
статистика, 5-9 кл. – М.: Дрофа, 2006.
 Бунимович Е.А. Вероятностно-статистическая
линия в базовом школьном курсе математики.Математика в школе, №4, 2002.
3000 задач с ответами по математике, - М.:
Экзамен, 2012
 Мордкович А.Г., Семенов П.В. События,
вероятности, статистическая обработка
данных.- Математика (приложение к газете
«Первое сентября»), №34, 35, 41, 43, 44,
48, 2002, №11, 17, 2003.
 Материалы с сайта www.1september.ru,
фестиваль педагогических идей «Открытый
урок»
 Материалы с сайта www.mathege.ru
