Балка опирается в двух точках
реклама
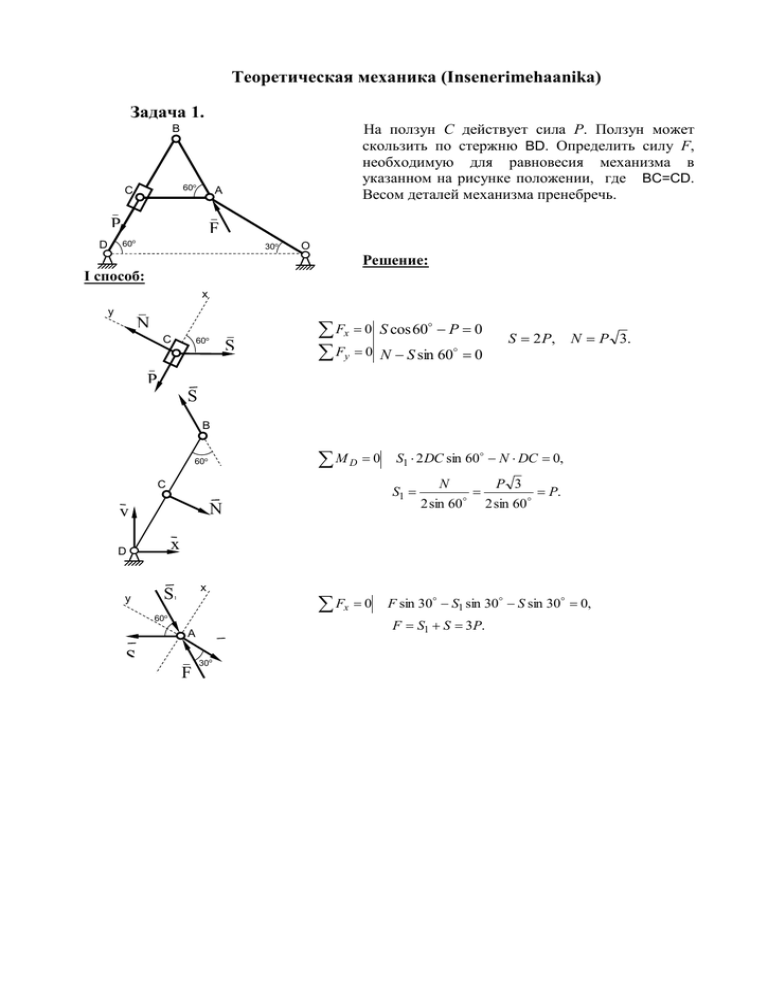
Теоретическая механика (Insenerimehaanika) Задача 1. На ползун С действует сила Р. Ползун может скользить по стержню BD. Определить силу F, необходимую для равновесия механизма в указанном на рисунке положении, где BC=CD. Весом деталей механизма пренебречь. B 60o C A P F 60o D 30o O Решение: I способ: x y N C 60o S Fx 0 Fy 0 S cos 60 P 0 N S sin 60 0 S 2 P, N P 3. P S ’ B MD 0 60o C S1 2 DC sin 60 N DC 0, S1 N ’ y D N 2 sin 60 P 3 2 sin 60 P. x D D y x S 60’ Fx 0 1 o F S1 S 3P. A S ’ F F sin 30 S1 sin 30 S sin 30 0, 30o S 2 II способ: Fs A cos 60 PsCr 0, SB s B cos 30 s A cos 60 , s B s A tan 30 , 30o B Src Sec P 60o 60o o 60 C D s A cos 60 sCr cos 60 sCe cos 30 , SA 1 2 s A sin 30 sCr sin 30 s B cos 30 , 60o 3 2 A sCr s A , F 30o O 3 Fs A sin 30 P s A 0, 2 F 3P. Ответ: F=3P. Задача 2. A Однородное весом G опирается в точках A и B на остроконечные призмы, с которыми у кольца одинаковый коэффициент трения. Найти при каком значении коэффициента трения кольцо будет находиться в равновесии при произвольно расположенным грузом С весом Р. Дано: G, P. Найти . B C Решение F T A Примем, что груз находиться в произвольном положении и изобразим силы, действующие на кольцо. Составим уравнения равновесия Fkx 0; FB TA 0 A A B T F O B B Fky 0; M o 0; TA r TB r P r sin 0 где r – радиус кольца. G B B FA GP 1 2 FA TB G P 0 C , P (G P) . FB B 2 1 Из последнего P sin В предельном случае TA FA , TB FB . Тогда из первых двух уравнений имеем (G P) 1 , откуда P sin . G P 1 sin 1 2 При этом значении кольцо находиться в состоянии предельного статического равновесия при любом значении угла . Принимая наибольшее значение sin 1 при / 2 , получим значение , которое обеспечивает равновесие при любом в интервале P 0 . G 2P P Ответ: . G 2P Задача 3. P P Однородный гладкий цилиндр, находящийся на гладкой плоскости, разрезан на две равные половинки и удерживаются в равновесии с помощью нити, перекинутой через цилиндр, на концах которых висят грузы. Общий вес цилиндра G . Найти минимальный вес грузов Р, при котором система будет в равновесии? Дано: G. Найти P. Решение P O C G/2 TA FA P Рассмотрим равновесие правой половинки цилиндра. В предельном случае обе части цилиндра пытаются отделиться друг от друга, соприкасаясь только в нижней точке А с силой ТА . Центр тяжести полуцилиндра находим по формуле центра тяжести сектора 2 sin / 2 4 r OC r , r - радиус цилиндра. 3 /2 3 Из уравнения равновесия имеем G 4 r M A 0; P r 2 P r 2 3 0 , 2 G что P . 3 2 G Ответ: P 3 Задача 4. Система состоит из однородного цилиндра 1 радиусом r и массой m1 , груза 2 массой m2 и нерастяжимой нити. В начальный момент система покоится, а груз находится на полу. В какой-то момент под действием пары сил с моментом М система начинает движение. Найти угловую скорость цилиндра в момент отрыва груза от пола. Первоначальная длина нити превосходит длину натянутой нити на величину l. Дано: r , m1 , m2 , 0 0 , l и M=const. Найти 2 . Решение 1 B M B C Решение состоит из двух этапов. 1. Первый этап заключается в нахождении угловой скорости цилиндра до момента отрыва груза от пола, когда выберется лишняя длина нити l , но нить еще не натянута. По теореме кинетической энергии имеем J 2 m r2 Ek Ek 0 Wke , Ek 0 0 , E k c 1 , J c 1 и 2 2 2 M l l Wke M r , где r . m1r 2 12 M l 2 M l откуда 1 . r m1r 2 2 r 2. Явление, когда нить полностью выпрямится и груз втечение очень малого времени получит какую-то скорость, называется ударом. По теореме кинетического момента при ударе LC1 LC0 M C I ke . Момент импульса внешних сил M C I ke при ударе равен нулю. Тогда m r2 J C 2 m 2 V2 r J C 1 0 , где V2 2 r и J C 1 . 2 m1 1 2 m1 M l Откуда 2 . m1 2 m2 r m1 2 m2 m1 r Ответ: 2 2 m1 M l r m1 2 m2 m1 r Задача 5. Два одинаковых стержня длиной l и весом G каждый соединены шарниром С в точках А и В опираются на гладкий горизонтальный пол. В начальный момент шарнир находится на высоте h от пола и начинает спускаться без начальной скорости. Определить скорость шарнира С в момент его первого соприкосновения с полом. C A B Решение: C T1 T0 We , mv 2 I 2 h 2 2G , 2 2 2 2 2 mv I mgh, 2 h A1 C1 A G B v v B1 mvc2 ml 2 v c2 mgh, 4 12l 2 3v c2 v c2 12 gh, v c 3 gh . vC Ответ: vc 3gh. Задача 6 Водило I длиной ОА=l вращается вокруг оси О неподвижного колеса 1 с угловой скоростью и угловым ускорением . На конце А водила шарнирно закреплено колесо z. Радиусы колес 1 и 2 соответственно r и R= 2r. Найти скорость и ускорение точки Р, находящейся на ободе колеса 2 в показанном на рисунке положении. Дано: ОА=l, , , r, R= 2r . Найти: v p и a p . 2 1 , А I р Решение: Методом остановки водила (метод Виллиса) найдем угловую скорость 2 колеса 2 2r r , 1r R где 2r и 1r - относительные угловые скорости колес, направленные в одну сторону 2 I r 1 I R или 2 0 r 1 2 . 2 2r 2 Это соотношение справедливо в любой момент времени, а значит угловое ускорение 2 2 . v A OA l . Скорость точки А водила Скорость точки Р по формуле плоского движения v p v A v pA , v pA 2 AP 2 R 2 2r 2r r . где 2 2 1 , vА 2,2 aA a An А I a npA р a pA vPА Откуда v p v A2 v pA 2 l 2 2 r 2 l 2 r 2 . 2 Соответственно усорения точки Р n a p a A a pA a pA , r Ap 2r 2 2 2 где n a pA 2 - нормальное ускорение в относительном 2 2 движении вокруг точки А, apA 2 Ap а касательное 2 2r r . Ускорение точки А a A a An a Aa , где a An I2OA 2l , a A I OA l . Окончательно ускорение точки Р ap Ответ: a n A a 2 a pA vp l 2 r 2 A a n 2 pA 2r 2 l r l 2 2 2 Задача 7 Жесткая конструкция, состоящая из двух одинаковых тяжелых однородных пластин, соединенных тонким невесомым стержнем с ломанной осью (изогнутом под прямым углом), удерживается в равновесии на опоре О. Найти максимальное значение l , при котором система находится в равновесии, если коэффициент трения стержня об опору равен . 4a l 4a 4a 3a 4a Решение: Найдем положение центра тяжести пластин. 2,6а 1,4а 2а у С1 х С2 2а С а 2а 3а а уС=0 ( в силу симметрии) xc где A1 xc1 A2 xc2 A1 A2 A1 4a 4a 16a 2 (площадь прямоугольника). 1 A2 3a 4a 6a 2 (площадь треугольника). 2 xc1 2a , x c2 3a (координаты центров тяжести прямоугольника и треугольника) 16a 2 2a 6a 2 3a 14a3 xc 1,4a . 16a 2 6a 2 10a 2 Если стержень, опирающийся на точку О оставить горизонтальным, то в случае равновесия сила трения на опоре О отсутствует. b=6,6a l А b-l C b=4a+2,6a=6,6a O G C’ G Из уравнения моментов относительно точки О M 0 0, G l G (b l ) 0 , l b l 0 , 2l b 6,6a , l 3,3a . Для нахождения максимального значения l несколько сдвинем стержень влево. В этом случае система повернется на некоторый угол и будет находиться в предельном равновесии с учетом силы трения на опоре О. Fn lmax F А b-lmax b C’ G у C G x Из условия равновесия имеем F F kx 0, G sin F G sin 0 , F 2G sin ky 0, Fn G cos G cos 0 , Fn 2G cos . 0, G cos l max G sin b G cos (b l max ) 0 . M 0 . cos l max sin b cos b cos l max 0 , 2l max cos b(sin cos ) , b(tg 1) . 2 в предельном случае равновесия F Fn , F Fn l max Учитывая, что получим sin cos , Тогда l max Ответ: tg . b 1 6,6a 1 3,3a1 2 2 lmax 3,3a1 Если 0,3 , то lmax 3,3a1 0,3 4,29a .
