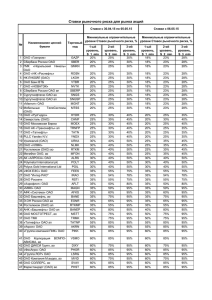
Разработка алгоритмов на базе FRiS

Разработка алгоритмов
на базе FRiS-функции
Лекция №6
Функция конкурентного сходства
F=(r2-r1)/(r2+r1)
F[-1, 1]
r2
r1
F=0
Компактность
 Существует множество нечетких,
интуитивных определений.
 Невычурность границ
 Простота форм
 Пример удачной формализации: профиль
компактности
Формулировка компактности
через FRiS-функцию
 Среднее значение конкурентного сходства для всех
объектов выборки ~ компактность выборки
F=0.87
F=0.38
F=0.03
•В зависимости от принципов по которым определяются ближайший
«свой» и «чужой» представители можно моделировать различные
виды компактности
•Похожесть на ближайшего соседа – локальная компактность
•Похожесть на типичного представителя – унимодальная и
полимодальная компактность
Плотность распределения FRiS-функции
в статистической постановке задачи
распознавания
2 pj ( z )  exp 2t  pj ( z ) , t  0
p Rj ( z ) (t ) n


0, t  0

2 p1( z )  p 2( z )

, 1  t  1

2
p F ( z ) (t ) n


 ((1  t ) p 2( z )  (1  t ) p1( z ))


0, иначе
p 2( z )
p1( z ) p1( z )  p 2( z )

2
p1( z )  p 2( z )
( p1( z )  p 2( z ))
2  p1( z )  p 2( z )  ln
EF ( z ) n


Зависимость ожидаемой величины FRiS-функции от
вероятности ошибочного распознавания
FRiS
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
Err
0,01
0,06
EF ( z ) 
0,11
0,16
0,21
0,26
0,31
0,41
Err
1  Err 
2
2 Err  (1  Err )  ln
(1  2 Err )
0,36
0,46
1
1  2 Err
Функция конкурентного сходства –
единый базис для решения различных
задач Data Mining
Таксономия
Построение решающего
правила
Выбор информативной
системы признаков
Обобщенная
классификация
Прогнозирование
Комбинированные задачи
FRiS-Tax
FRiS-Stolp
FRiS-GRAD
FRiS-TDR
FRiS-Pro
FRiS-SDX
Алгоритм FRiS-Stolp
 Ищется базовое множество столпов,
состоящее из наилучшего кандидата на
роль столпа образа А и наилучшего
кандидата на роль столпа образа В.
 Считается, что рассматриваемый образ описывается
единственным столпом, а в качестве столпа
конкурирующего образа берется ближайший объект из
этого образа.
 Происходит наращивание базовой
системы столпов до достижения одного
из условий остановки
 заданный уровень точности распознавания обучающей
выборки
 максимально допустимое количество столпов в системе
Алгоритм FRiS-Stolp
r1
r2
r2
r1
Алгоритм FRiS-Tax
 Редуцированная FRiS-функция
 Виртуальный конкурент
 Работа алгоритма состоит из двух этапов:
 FRiS-Cluster
 Отыскиваются центры локальных сгустков объектов
(столпы).
 Выборка распределяется между столпами. Строится
кластеризация.
 FRiS-Class
 Линейно разделимые кластеры объединяются в таксоны
сложной формы.
Выбор числа таксонов в алгоритме FRiS-Tax




Строятся кластеризации для всех k  K, вычисляется их качество
F(2),F(3),…,F(k)
Ищутся локальные максимумы качества

такие k, что F(k-1)<F(k)&F(k+1)<F(k)
Этап FRiS-Class выполняется лишь для тех k, которые соответствуют
локальным максимумам FRiS-функции.
Выбирается вариант таксономии с максимальным значением FRiS-функции.
0,53
Fs(k)
0,51
0,49
0,47
0,45
0,43
0,41
0,39
2
3
4
5
6
7
8
9
10
11
13
14
15 k
Требования к обобщенной
классификации
 Решает задачи распознавания,
таксономии и частичного обучения
 Смесь классифицированной и
неклассифицированной выборок
разбивается на таксоны
 алгоритм ТРФ
 Геометрическая компактность
 объекты одного таксона должны быть похожими
друг на друга и отличаться от объектов других
таксонов
 Однородность
 в одном таксоне должны преобладать объекты
одного и того же образа
Вычисление FRiS-функции по
смешанной выборке
z VA
r1  min
{ ( z , x)}
A
C
xV V
r2  min{ r*, minB { ( z , x)}}
xV
r1
r2
r1  min
{ ( z , x)}
B
C
z  VB
xV V
r2  min{ r*, minA { ( z , x)}}
xV
Vmix  V A  VB  VC
r* - расстояние до виртуального конкурента
z  VC
r1 
min
xV A V B V C
{ ( z , x)}
r2  min{ r*, max{ rA , rB }}
Вычисление FRiS-функции по смешанной
выборке с опорой на столпы
z VA
r1  minA { ( z , x)}
xS
r2  min{ r*, minB { ( z , x)}}
xS
FSmix  1
Vmix
mix
F
 ( z )  max
r1 S minB { ( z , x)}
zVv Vu
z  VB
xS
r2  min{ r*, minA { ( z , x)}}
xS
S  S A  SB
z  VC
r1  min
{ ( z , x)}
A
B
xS  S
r2  min{ r*, max{ rAS , rBS }}
Схема алгоритма FRiS-TDR
 Ищется базовое множество столпов, состоящее
из наилучшего кандидата на роль столпа образа
А и наилучшего кандидата на роль столпа
образа В.
 Считается, что рассматриваемый образ описывается
единственным столпом, а в качестве столпа конкурирующего
образа берется ближайший объект из этого образа.
 Объекты неклассифицированной выборки могут быть столпами
как образа А, так и образа В.
 Происходит наращивание базовой системы
столпов до достижения одного из условий
остановки
 заданный уровень точности распознавания обучающей выборки
 максимально допустимое количество столпов в системе
 F(i-1)<F(i ) и F(i+1)<F(i )
Эффект от использования
информации из распознаваемой
выборки
Примеры работы алгоритма на
классифицированной и
неклассифицированной выборках
Автоматический выбор числа
таксонов
0,65
0,6
0,55
0,5
0,45
0,4
2
3
4
5
6
7
8
9
10
11
12
Задача SDX
 Необходимо привести
неструктурированный массив данных к
виду, удобному для восприятия
человеком
 Сокращение числа объектов (переход к
эталонам)
 Сокращение числа признаков (переход
к существенным)
Алгоритм FRiS-SDX
Обучающая
выборка
<A,X>
Y *  arg max  FX (a, c* | c*  arg min Y (a, c))
a A
cCY*
CY*  arg max (  FY (a, c* | c*  arg min Y (a, c))
C  A, a A
|C| m*
Выбор системы
признаков
(алгоритм GRAD)
cC
Таксономия+
Решающее правило
(алгоритм FRiS-Tax)
Оценка
предсказательной
способности