Золотое сечение Урок математики в 6 классе Учитель: Майорова Т.Г.
реклама

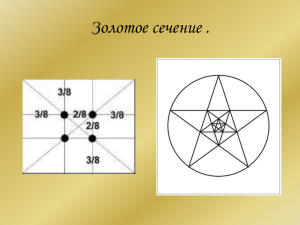
Золотое сечение Урок математики в 6 классе Учитель: Майорова Т.Г. «Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает.» Н.Винер. • “Великая книга природы написана на языке математики”. • Г. Галилей – ученый 16 века, основоположник естествознания – науки о природе. Пропорция • Слово «пропорция» означает «соразмерность», «определенное отношение частей между собой». • Учение об отношениях и пропорциях особенно успешно развивалось а IV в. До н.э. в Древней Греции. • С пропорциями связывались представления о красоте, порядке и гармонии. • Теория отношений и пропорций была подробно изложена в «Началах» Евлида, там, в частности, приводится и доказательство основного свойства пропорции. Евклид • Евкли́д или Эвкли́д ( ок. 300 г. до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в 3 в. до н. э. • Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета. • С давних пор ученые занимались поисками гармонии и совершенства. Одним из таких вопросов был деление отрезка таким образом, чтобы отношение частей было совершенным. • Задолго до нашей эры, в различных точках мира, разные ученые, независимо друг от друга, находили это отношение, и у всех это отношение было одним и тем же. • И сейчас мы с вами найдем такое деление отрезка, таким способом, каким его нашел знаменитый ученый Пифагор. Пифагор • Пифагор Самосский ( 570490 гг. до н. э.) — древнегреческий фи лософ, математик и мистик, создатель религиознофилософской школ ы пифагорейцев. А С В АС 0,6 Золотая пропорция Такую пропорцию, где меньшее так АС ВС ВС относится к большему, как большее к целому, назвали золотой пропорцией. А ВС АВ ВС деление отрезка в таком отношении – 0,6 золотым сечением АВ Этот пятиугольник называется пентаграммой, знак школы Пифагора. Во времена Пифагора он считался магическим. Отношение частей его диагоналей, названное золотым сечением, и приближенно равное 0,6, а более точно 0,618, считалось идеальным. Золотой прямоугольник а b a 0,618 b Золотой прямоугольник обладает замечательным свойством: если от золотого прямоугольника отрезать квадрат со стороной равной ширине, то оставшийся прямоугольник также будет золотым. Спираль Архимеда. Золотое сечение в природе Золотое сечение в анатомии Джоконда Леонардо Давинчи Аполлон Бельведерский Парфенон. Это здание построено в 5 веке до н.э. зодчим Иктином, в честь богини Афины. Это здание – символ Греции, тоже построено по принципу золотого сечения. Оно считается совершеннейшим из архитектурных сооружений. Отношений высоты здания к его длине равно приближенно 0, 618. По вертикали здание также делится по золотому сечению с точностью до тысячных!!! Деревянные храмы в Кижах. Георгиевский зал Кремлевского Дворца. Золотая пропорция вокруг нас. Золотая пропорция в космосе Подведем итоги: • С каким новым понятием вы познакомились? • какому значению приближенно равно значение золотого сечения? • какой прямоугольник называет золотым? • откуда взялось такое название – золотое сечение? • где в жизни мы встречаемся с золотым сечением и золотым прямоугольником? • как эти знания могут пригодиться в жизни? • как вы понимаете эпиграф к нашему уроку?