Задача Д39

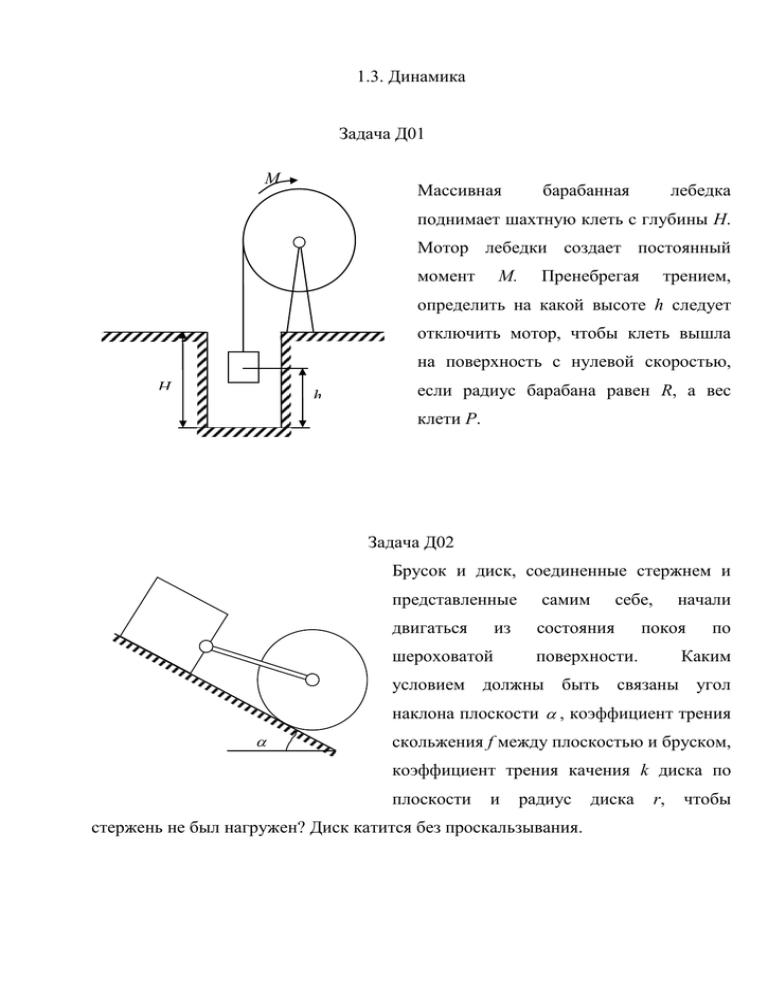
1.3. Динамика
Задача Д01
M
Массивная
барабанная
лебедка
поднимает шахтную клеть с глубины H.
Мотор лебедки создает постоянный
момент
M.
Пренебрегая
трением,
определить на какой высоте h следует
отключить мотор, чтобы клеть вышла
на поверхность с нулевой скоростью,
H
h
если радиус барабана равен R, а вес
клети P.
Задача Д02
Брусок и диск, соединенные стержнем и
представленные
самим
двигаться
состояния
из
шероховатой
себе,
начали
покоя
поверхности.
по
Каким
условием должны быть связаны угол
наклона плоскости  , коэффициент трения

скольжения f между плоскостью и бруском,
коэффициент трения качения k диска по
плоскости
и
радиус
стержень не был нагружен? Диск катится без проскальзывания.
диска
r,
чтобы
Задача Д03
Тело, имеющее форму цилиндра радиусом
r, имеет массу m и момент инерции
C
r
a
относительно
оси
цилиндра
J.
Центр
тяжести цилиндра смещен на величину a от
О
его
оси.
Цилиндр
положен
на
горизонтальную плоскость так, что его
центр
тяжести
занимает
наивысшее
положение. Вследствие небольшого толчка
цилиндр катится без скольжения. Определить скорость оси цилиндра в момент,
когда его центр тяжести занимает низшее положение.
Задача Д04
r
V0
Вычислить кинетическую энергию гусеницы
трактора, движущегося со скоростью V0 . Расстояние
между осями колес l , вес одного погонного метра
l
гусеничной цепи -  .
Задача Д05
Тяжелый однородный цилиндр, получив ничтожно
C
малую начальную
α C1
скольжения с горизонтальной площадки AB , край
которой
A
B
скорость, скатывается без
заострен
и
параллелен
образующей
цилиндра. Радиус основания цилиндра
r. В
момент отделения цилиндра от площадки плоскость, проходящая через ось
цилиндра и край B , отклонена от вертикального положения на некоторый угол
CBC1   . Определить угловую скорость цилиндра в момент отделения его от
площадки, а также угол  . Трением качения и сопротивлением воздуха
пренебречь.
Задача Д06
B
2l
C
Стержень AB длиной 2l падает, скользя концом A по
гладкому горизонтальному полу. В начальный момент
стержень занимал вертикальное положение и находился в
h
A
покое. Определить скорость центра тяжести стержня в
зависимости от его высоты h над полом.
Задача Д07
A
М
Тяжелая стальная отливка весом Р прикреплена к
стержню, который может вращаться без трения вокруг

неподвижной оси О. Отливка падает из наивысшего
O
положения А с ничтожно малой начальной скоростью.
Пренебрегая массой стержня, определить наибольшее
давление на ось, а также зависимость давления от угла
.
Задача Д408
Космический аппарат (КА) вращается с угловой
скоростью 0. Определить, какую полную работу


должен совершить двигатель маховика, чтобы
остановить вращение космического аппарата, считая,
что вращение КА происходит вокруг поступательно перемещающейся оси,
проходящей через его центр масс. Ось вращения маховика совпадает с осью
вращения аппарата; I и I0 – момент инерции маховика и аппарата (вместе с
маховиком) относительно общей оси вращения.
Задача Д09
Однородная тяжелая балка AB длиной 2l
A
B
2l
и весом Q при закрепленных концах находится
в горизонтальном положении. В некоторый
момент конец A освобождается и балка начинает падать, вращаясь вокруг
горизонтальной оси, проходящей через конец B; в момент, когда балка становится
вертикальной, освобождается и конец B. Определить в последующем движении
балки траекторию ее центра тяжести и угловую скорость ω.
Задача Д10
В цирке Шапито мотоциклист едет по внутренней поверхности сферы
радиуса r. Траектория мотоциклиста – окружность радиуса R, лежащая в
горизонтальной плоскости. Выяснить, при каких скоростях траектория в нижней
полусфере будет устойчивой, если коэффициент трения шин о поверхность сферы
равен k.
Задача Д11
Деревянная доска длинной l и весом Р может
О1
вращаться без трения вокруг горизонтальной оси ОО1. В
О
середину доски углубляется пуля, летевшая
V0
l
перпендикулярно к ней со скоростью V0. Определить
угловую скорость, которую приобретает доска в момент попадания пули, если вес
пули равен Р1.
Задача Д12
Груз весом Р подвешен на нерастяжимом
однородном тросе длиной l, навитом на
цилиндрический барабан с горизонтальной осью
вращения. Момент инерции барабана относительно
x0
оси вращения I, радиус барабана R, вес единицы
x
длины троса р. Определить скорость груза в
момент, когда длина свисающей части троса равна
x, если в начальный момент скорость груза равна
нулю, а длина свисающей части троса была x0. Трением на оси барабана,
толщиной троса и изменением потенциальной энергии троса, навитого на
барабан, пренебречь.
Задача Д13
В эпициклическом механизме бегающая
r1
M
O
O1
шестеренка радиуса r1 насажена на кривошип
с противовесом, вращающийся вокруг оси
неподвижной шестеренки под действием
приложенного момента M. Определить
угловое ускорение вращения кривошипа и
окружное усилие S в точке касания
шестеренок, если расстояние между осями
шестеренок равно l, момент инерции кривошипа с противовесом относительно
оси вращения кривошипа равен I0, масса бегающей шестеренки m1, момент
инерции шестеренки относительно ее оси I1. Трением пренебречь. Центр тяжести
шестеренки и кривошипа с противовесом находится на оси вращения O
кривошипа.
Задача Д14
Три шарика одинаковой массы m
О
l
прикреплены к нижним концам сварной
l
стержневой конструкции, имеющей возможность
l
l
l
вращаться вокруг горизонтальной оси О,
перпендикулярной плоскости чертежа.
Пренебрегая размерами шариков и массой
конструкции, определить частоту малых колебаний системы, если l задано.
Задача Д15
Основной частью прибора, используемого для
измерения моментов инерции деталей, является
колебательная система, состоящая из легкой рамки
1
1, в которой закрепляется деталь 2, и спиральной
пружины. Последовательно замеряют периоды
2
колебаний: T1-одной рамки, T2- рамки с эталоном,
момент инерции IЭ которого известен, и T3- рамки с
деталью. Найти с помощью перечисленных данных
момент инерции детали относительно оси,
проходящей через опоры рамки.
Задача Д16
B
A

a
C
С каким ускорением a должен двигаться
треугольник ABC с острым углом, чтобы груз
поднимался вверх по AB? Коэффициент трения груза о треугольник равен f.
Задача Д17
По какой плоской кривой следует изогнуть трубку, чтобы
помещенный в нее в любом месте шарик оставался по
отношению к трубке в равновесии, если она вращается с
постоянной угловой скоростью  вокруг оси 0y ?
y

x
Задача Д18
Цилиндр радиуса 2a имеет отверстие радиуса a ; сечение
цилиндра
показано
на
рисунке.
Цилиндр
может
перекатываться по плоскости без скольжения. Найти период
малых колебаний цилиндра.
O`
O
Задача Д19
Цилиндр радиусом r и массой m может
катиться без скольжения по горизонтальной
плоскости. Две одинаковые пружины
O
а
r
жесткости с прикреплены посередине его
длины на расстоянии a от плоскости;
противоположные концы пружин закреплены.
Определить период малых колебаний
цилиндра.
Задача Д20
Металлическая цепь длиной l
l
удерживается на гладкой наклонной
плоскости с помощью гвоздя. В некоторый

момент гвоздь выдергивают. Определить
скорость цепи в момент, когда она полностью соскользнет на горизонтальную
плоскость, если =1.
Задача Д21
Центру масс С однородного катка
С
весом P радиуса R сообщают начальную
скорость V0. Коэффициент трения качения k.
К точке С шарнирно крепиться однородный
стержень весом Q, который скользит по плоскости. Длина стержня l, коэффициент
трения f. Какой путь пройдет каток до остановки?
Задача Д22
Проволока, выгнутая по параболе y  h  cx 2
расположена в вертикальной плоскости. Из вершины
A параболы начинает перемещаться кольцом М весом
Р. Какую начальную скорость V0 следует сообщить
кольцу в точке А, чтобы при последующем движении
оно не оказывало давления на проволоку?
y
A
M
O
B
Задача Д23
Однородный цилиндр положен на наклонную
плоскость. При каких углах  цилиндр будет катиться без
скольжения, если коэффициент трения скольжения равен
 . Трением качения и сопротивлением воздуха
пренебречь.

А

А
А
Е
Е
А
Е
С
В
l
Е
D
l
2
Задача Д24.
Однородный стержень длиной l и весом P
удерживается в горизонтальном
положении двумя нитями. Точка С –
центр тяжести стержня. В момент обрыва
нити АВ определить натяжение N нити
ED, закреплённой на стержне в точке D и
составляющей с горизонтом угол  , если
4
l
4
CD 
Задача Д25.
Однородная пластина, имеющая форму
прямоугольного
треугольника,
гипотенуза которой равна 12 см,
поставлена на гладкую горизонтальную
плоскость
так,
что
гипотенуза
перпендикулярна ей. Предоставленная
затем самой себе пластинка падает под
влиянием силы тяжести. Определить,
какую кривую описывает при этом точка
М – середина стороны ВС.
y
B
1
l.
4
M

C
A
x
x
y
A
90°
B
α
Ao
Задача Д26.
Ползуны A и B одинакового веса P, шарнирно соединенные невесомым
стержнем (AB=l), могут скользить без трения по взаимно перпендикулярным
направлениям. Ползун A отводится в положение Ao, в котором ему сообщается
начальная скорость Vo вдоль оси Ax. Считая, что α=60°, определить: 1) при какой
минимальной скорости Vo стержень достигает горизонтального положения; 2)
усилие в стержне в этот момент.
Задача Д27
Гантелька состоит из двух шариков (A,B) и соединяющего их
A
тонкого невесомого стержня длины l. Гантелька стоит в углу,
образованном гладкими плоскостями. Нижний шарик B
гантельки смещают горизонтально на очень маленькое
B
расстояние, и гантелька начинает двигаться – шарик B вправо,
шарик A вниз вдоль стены. Найти скорость нижнего шарика в
этот момент, когда верхний оторвется от вертикальной плоскости. Считать, что
верхний и нижний шарики имеют равные массы, размерами их пренебречь.
Задача Д28
n об/мин
Р
Барабан электролебедки диаметром 0,32 м после
включения тока начинает вращаться равноускоренно. Через 4
секунды барабан делает 60 об/мин. Определить натяжение N
наматываемого на барабан каната, поднимающего груз P=20 kH.
Задача Д29

A
Q 
b
Q
Невесомый стержень АВ длиной  , на конце которого
находится точечная масса m, закреплен с помощью
цилиндрического
шарнира
на
вертикальной
оси,
вращающейся с угловой скоростью  . При отклонении
стержня АВ на малый угол  0 от положения относительного

равновесия он начинает колебаться около этого положения с
круговой частотой, равной   sin  , где  - угол, при
котором имеет место относительное равновесие. Найти
B добавочные гироскопические давления на подшипники в
Q момент прохождения стержнем положения относительного
равновесия. Расстояние между подшипниками равно b .
y
Задача Д30.
C
A
Материальная точка массы m
начинает двигаться без начальной
a
скорости из точки A по гладкой
P
направляющей,
x
O
y  a cos
a
B
уравнение
которой
2 x
.
l
Определите силу давления точки
l 2
на направляющую в тот момент, когда
l 2
она проходит через точку B.
Задача Д31.
y
A
Точка M массой m скользит
B

вдоль
M
K
a
полуокружности
внутри призмы, движущиеся вдоль
mg
O
гладкой
оси Ox с постоянным ускорением a.
x
Определить давление на призму
точки M в нижнем положении K, если в верхнем положении A относительная скорость
точки равна нулю.
Задача Д32.
y
z
Шарик массой m запускают в точке
A
O со скоростью V0 в покоящуюся
горизонтально расположенную трубку
OAB, прикрепленную к вертикальной
O
оси.
V0
Момент
относительно
B
инерции
оси
вращения
I z  I , OB  2r .
x
С
относительной
скоростью
вылетит
трубки?
из
трубки
равен
какой
шарик
Трением
пренебречь.
Задача Д33
Однородный цилиндрический каток
массой
O1
A
r
скатывается
без скольжения по цилиндрической
30o
O
m и радиусом r
A
h
4r
поверхности радиусом
4r тела B
масса которого равна 5m . В начальный
момент времени оба тела покоились и
B
оси
составляющей
когда ось
30o
O и O1 находились на прямой,
с горизонталью. Определить скорость тела
B в тот момент
O проходит низшее положение. Трением тела B о неподвижную
горизонтальную поверхность пренебречь.
Задача Д34
Три одинаковых трубы радиусом
r находятся
в равновесии в неподвижно закрепленной
1
R
трубе радиусом
r
2
3
R , располагаясь в два ряда.
Все трубы малого радиуса касаются друг
друга, при этом трубы нижнего ряда касаются
также трубы большего радиуса. Найти
наибольшее значение R , при котором
равновесие системы ещё возможно.
2
Задача Д35
К клину весом
B
P1 , расположенному на
гладкой горизонтальной плоскости,
1
приложена постоянная сила
F
A
стержня
F . Вес
AB  P2 . Считая угол 
известным и пренебрегая весом ролика,

определить скорость клина в зависимости
от пройденного пути
S , если его
начальная скорость равнялась нулю.
Задача Д36
А
B
D0
Два однородных прямолинейных стержня
АВ и ВD массы m и длины
связаны
посредством
 каждый
шарнира
В.
Определить реакции жесткой заделки А
D
стержня
АВ,
когда
опущенный
без
начальной скорости из горизонтального
положения BD0 стержень BD повернется на угол 900 под действием силы тяжести.
Трением в шарнире В пренебречь.
ЗадачаД37
Веревка, закрепленная одним концом на барабане 1,
несколько
раз
наматывается
на
него,
далее
перебрасывается через неподвижный блок 2, и затем
2
прикрепляется в точке А к платформе 3. Барабан и блок однородные цилиндры радиуса r и веса Р, вес платформы
Q. К барабану приложен вращательный момент М=const.
М
Считая, что платформа движется поступательно и веревка
1
не проскальзывает по блоку, найти ускорение, с которым
3
А
будет подниматься платформа.
Задача Д38
Сплошной однородный диск радиуса r скреплен с тонким
В
однородным стержнем АВ. В положении, указанном на
рисунке, диск находится в покое. При незначительном
2r
А
отклонении стержня от вертикали диск вместе со стержнем
r
под действием силы тяжести начинает катиться по
плоскости без скольжения.
Определить скорость конца В стержня в момент удара о плоскость. Вес стержня и
диска считать одинаковыми. Длина стержня 2r. Трением качения пренебречь.
М
О
А
φ
С
В
Задача Д39
Два однородных стержня (ОА длиной а, весом Р и АС
длиной b, весом Q) соединены шарниром А и находятся в
вертикальной плоскости. Стержень ОА укреплен
шарнирно, а стержень АС проходит через гладкую муфту
В.
Определить
уравновешивающий
момент
М,
удерживающий стержень ОА в горизонтальном положении под углом
стержню АС.
V2
B
φ
к
Задача Д40
Два обруча радиуса r катятся без скольжения
по направляющей в разные стороны. Скорости
центров А и В обручей постоянны и равны
соответственно V1 и V 2 . Определить ускорение
кольца М, надетого на два обруча, в зависимости от
угла φ.
M
V1
A
φ
Задача Д41
Материальная точка опускается под действием силы тяжести по гладкой
кривой, расположенной в вертикальной плоскости. При этом она удаляется от
горизонтали, проходящей через ее начальное положение, с постоянной скоростью c.
Выбрав начало координат в начальном положении точки, найти уравнение этой
кривой. Принять горизонтальную составляющую скорости в начальный момент
времени равной нулю.
K
O
A
Задача Д42
Стержень ОА, момент инерции которого
относительно оси z равен J, вращается вокруг
этой оси. При этом свободно надетое на
стержень колечко K скользит по стержню с
постоянным относительным ускорением а.
В начальный момент времени OK=l и
относительная скорость колечка равно нулю.
Определить:1)угловую скорость  , угловое
ускорение  стержня как функции времени и
закон вращения стержня, 2) составляющие
реакции стержня на колечко, 3)вращающий
момент Мвр. Трением пренебречь.
R
r

P
Задача Д43
Однородный круглый цилиндр радиуса R и веса Q
имеет цилиндрический выступ, радиус которого r , и
удерживается в равновесии на шероховатой наклонной
плоскости силой трения и весом P груза, привязанного
к свободному концу нити, намотанной на выступ.
Найти условия, при которых возможно равновесие, а
также вес P уравновешивающего груза и давление
цилиндра на плоскость при равновесии, если угол
наклона плоскости равен  , а коэффициент трения
равен f.
Задача Д44
Однородному стержню длиной 2l, лежащему на горизонтальной плоскости,
сообщена угловая скорость 0 вокруг оси, перпендикулярной к стержню и
проходящей через его центр. Определить время вращения стержня до остановки,
считая его давление на плоскость равномерным, а коэффициент трения о
плоскость равным f.
Задача Д45
Гладкий
А
Г-образный
стержень
вращается
в
горизонтальной плоскости вокруг вертикальной оси,
В проходящей через конец стержня О, с постоянной

О
угловой скоростью  . Муфта В массой m прикреплена
к стержню в точке А при помощи пружины с
жесткостью с. Длина недеформированной пружины l0 .
При
каких
условиях
равновесие муфты.
имеет
место
относительное