Лекция №7 Уравнение Клайперона-Клаузиуса

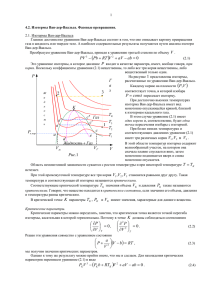
Лекция №7
Уравнение Клайперона-Клаузиуса
Исходя из общих условий равновесия, можно получить некоторые общие
соотношения, имеющие место при сосуществовании фаз. Рассмотрим, для
конкретности, сосуществующие жидкую и паровую фазы. Условия равновесия
сводятся к равенству температуры, давления и химических потенциалов в
сосуществующих фазах. Так как химические потенциалы жидкой (  L ) паровой
( G ) фаз сами являются функциями давления и температуры, то условие
равновесия сводится к виду
L  P,T   G  P,T 
Это уравнение определяет зависимость давления от температуры на линии
сосуществования жидкости и пара: Psaturation T  . Продифференцируем условие
равенства химических потенциалов по температуре, учитывая, что химические
потенциалы фаз зависят от температуры как явно, так и не явно, через
зависимость от температуры давления насыщения Psaturation T  .
   L     L  d Psaturation T    G    G  d Psaturation T 

.

 

 


T

P
d
T

T

P
d
T

P 
T

P 
T
Из общих термодинамических соотношений имеем
 
 

 v , а 
 s

T

P

P

T
Отсюда
 s L  vL

d Psaturation T 
dP
T 
  sG  vG saturation
dT
dT
d Psaturation T  sG  sL

dT
vG  vL


d Psaturation T 
q

dT
T  vG  vL 
Здесь q  T  sG  sL  - скрытая теплота перехода жидкость-пар. Это выражение,
q
определяющее связь давления насыщения со скачками энтропии  s   sG  sL и
T
объема v  vG  vL в сосуществующих фазах, является совершенно общим и
абсолютно точным. Выражения такого типа всегда имеют место, когда мы
сталкиваемся с, так называемыми, фазовыми переходами 1 – го рода. Изучению
этих явлений у нас будет посвящен отдельный курс. Сейчас же рассмотрим
случай, когда плотность паровой фазы, во-первых, много меньше плотности
сосуществующей с этим паром жидкости, или, что то же самое vG vL а, вовторых, сама по себе столь низка, что пар может рассматриваться как идеальный
газ. Тогда получаем
d Psaturation T 
q

dT
TvG
Подставляя vG из уравнения состояния идеального газа vG  RT P , получаем
d Psaturation
q

dT
Psaturation
RT 2
Откуда, предполагая, что теплота перехода q не зависит от температуры,
получаем, что
Psaturation
exp   q RT  ,
т.е. давление насыщенного пара убывает экспоненциально при стремлении
температуры к нулю.
1. Равновесие фаз с искривленной поверхностью
 A   P1  V1  P2  V2    S
Т.к.  V1    V2 , получаем
 A    P1  P2   V1    S
При механическом равновесии  R  0 . Т.е.
 P1  P2  V1    S
Для капли жидкости в паре получаем
4
V1   R 3 ; S  4  R 2
3
P1  P2 
2
R
Это разность давлений. Условие равновесия по отношению к обмену
частицами между каплей и газом:
1  P1 , T   2  P2 , T 
Условие равновесия по отношению к обмену частицами между каплей и
газом над плоской поверхностью:
1  P0 , T   2  P0 , T 
Вычитая, получим:
1  P1 , T   1  P0 , T   2  P2 , T   2  P0 , T 
 1 
 2 

  P1  P0   
  P2  P0 

P

P

T

T
v1  P1  P0   v2  P2  P0 
Отсюда
2  v2
2  v1
;  P2 
R v2  v1
R v2  v1
Условия равновесия однокомпонентных флюидов
 P1 
Известно, что в равновесии давление  P  и химический потенциал   
постоянны вдоль системы. Следовательно, если мы хотим написать условия
равновесия в явной форме, мы должны:
а) найти зависимость этих величин от температуры и объема (или плотности)
P T , v  и  T , v  ;
б) записать условия равенства давлений и химических потенциалов в фазах:
P T , vL   P T , vG  ;  T , vL    T , vG  .
в) считая, что температура системы задана, а давление и химический
потенциал являются известными функциями температуры и объема, решить
систему двух уравнений с двумя неизвестными: vL и vG .
Если нетривиальное решение этих уравнений существует, система находится в
двухфазном состоянии. Если такое решение не существует, мы имеем однофазное
состояние.
В случае, когда нетривиальное решение существует, подставляя найденные
корни в выражение для давления, получим соответствующее значение давление
Pcxc T  . Это давление называется давлением насыщения.
Покажем, как реализуется указанная схема на практике. Из определения
свободной энергии имеем
d F   S dT  P dV   d N
Соответственно,
P     F V T , N ;
    F  N T , V
Поэтому, если выражение для свободной энергии известно, можно считать
известными и зависимости давления и химического потенциала от температуры и
объема, а, следовательно, и уравнения, определяющие сосуществование фаз. В
общем случае выражение для свободной энергии должно находиться из
статистической физики. Если не считать очень небольшого числа простейших
случаев, задача вычисления свободной энергии чрезвычайно сложна. Мы будем
говорить об этом позднее. С другой стороны, задача вычисления свободной
энергии становится совершенно элементарной, если считать, что уравнение
P  P T , v  нам известно. (например, из эксперимента или
состояния системы
из каких-нибудь физических соображений). Тогда свободная энергия находится
простым интегрированием,
F T ,V     PT ,V  dV  N f T 
а химический потенциал соответствующим дифференцированием
 T , v     F  N T , V .
После этого уравнения сосуществования
P T , vL   P T , vG  ,  T , vL    T , vG .
записываются в явной форме.
2. Уравнение ван-дер-Ваальса
Проиллюстрируем описанную процедуру на примере уравнения ван-дер-Ваальса.
RT N
aN 2
P
 2 .
V  bN
V
Это уравнение содержит два не универсальных параметра a и b . Слово «не
универсальные» означает, что указанные параметры зависят от характера
взаимодействия молекул в той или иной жидкости, и, соответственно, различны в
различных жидкостях. При этом параметр a характеризует эффективное
притяжение между молекулами, а b определяет их эффективное отталкивание.
Критическая точка уравнения ван-дер-Ваальса (определение параметров
b ).
a
и
По определению критической точки имеем
 P
 v T  
RTc
 vc  b 
2

2a
 0;
vc3
 P  v 
2
2
T

2 RTc
 vc  b 
3

2a
0
vc4
Из этих двух уравнений нетрудно найти критические параметры vc , Tc .
vc  3b; RTc 
Подставляя найденные значения
критическое давление Pc
Pc 
8 a
.
27 b
vc , Tc в уравнение
ван-дер-Ваальса, найдем
1 a
27 b 2
В этом месте необходимо сказать несколько общих слов, имеющих отношение к
любому двухпараметрическому уравнению состояния типа уравнения ван-дерВаальса. Критические параметры любой жидкости vc , Tc , и Pc могут быть
получены из эксперимента. Если критические параметры vc , Tc , и Pc известны,
приведенные выше выражения могут рассматриваться как уравнения для
определения двух неизвестных величин a и b . Однако, три уравнения с двумя
неизвестными в общем случае решения не имеют.
Это означает, что в общем случае невозможно найти два таких параметра a и b ,
которые давали бы правильные значения трех критических параметров vc , Tc , и
Pc для данной жидкости.
Кривая сосуществования в переменных температура-объем
Из определения свободной энергии F T ,V     PT ,V  dV  N f T  имеем
 V  bN
F T ,V    RT N ln 
 N
2
 2a N
 N f T  ,

V

Соответственно, для химического потенциала     F  N T , V , получаем

v  2a
V 


 f T  ,  v  

v  b
v
N


Отсюда уравнения, определяющие сосуществование фаз, имеют вид
 T , v    k BT ln  v  b  
a
RT
a
 RT



;
2
2
v  b v
v

b
v
 L
L
G
G



 RT ln  vL  b   vL   2 a  RT
vL  b  v L



vG  2 a
ln  vG  b  

v

b
G

 vG
Аналитически решить эти уравнения невозможно. Численное же решение требует
задания температуры и индивидуальных параметров той или иной жидкости, a и
b.
Кривая сосуществования в переменных температура-давление
Подойдем к проблеме вычисления кривой сосуществования фаз немного с другой
стороны. Очевидно, что уравнение ван-дер-Ваальса может быть переписано в
виде
k T a
a

v3  v 2  b  B   v  b  0
P  P
P

С математической точки зрения это уравнение является кубическим уравнением
относительно мольного объема ( v ). Как всякое кубическое уравнение, оно имеет
либо один, либо три действительных корня. Можно показать (вам придется
сделать это самостоятельно), что три действительных корня существуют только,
если температура системы ниже критической T  Tc .
Легко записать выражения для этих корней с помощью формул Кордано. При
этом максимальный корень соответствует паровой фазе vG  P, T  , минимальный
корень соответствует жидкой фазе vL  P, T  , а промежуточный не имеет
физического смысла.
Подстановка корней vG  P, T  и vL  P, T  в выражение для химического
потенциала

 T , v    RT ln  v  b  

v  2a

 f T 
v  b 
v
дает химические потенциалы паровой и жидкой фаз G  P, T    T , vG  P, T   and
L  P, T    T , vL  P, T   . Соответственно, условие сосуществования фаз имеет
вид
G  P, T    L  P, T 
Это уравнение дает связь между давлением и температурой на кривой
сосуществования Pcxc T  , т.е. давление насыщения как функцию температуры.
Подставляя давление насыщения Pcxc T  в выражения vG  P, T  и vL  P, T  ,
получим температурную зависимость мольных объемов сосуществующих фаз.
Так же как и в предыдущем случае, реализовать описанную процедуру в
аналитическом виде невозможно. Однако, это вполне возможно сделать численно,
что вам и предстоит реализовать для различных алканов. На рисунке 2
представлены результаты такого расчета для этана.
Рис.2
Сплошными красными линиями представлены результаты расчета по уравнению
ван-дер-Ваальса, а точки соответствуют экспериментальным данным.
Из рисунка 2 видно, что точность описания экспериментальных данных в рамках
уравнения ван-дер-Ваальса довольно низкая. Тем не менее, уравнение ван-дерВаальса, будучи первой успешной теорией жидкости, несомненно является одним из
выдающихся достижений своего времени. В скобках замечу, что тысячи работ,
последовавших за теорией ван-дер-Ваальса, не внесли ничего принципиально
нового в понимание физики жидкостей. Исключение составляет построенная в
последней четверти двадцатого века флуктуационная теория критической точки, о
которой мы будем много говорить в дальнейшем.