Лекция 16. Влияние температуры

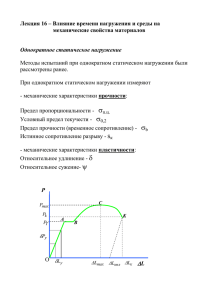
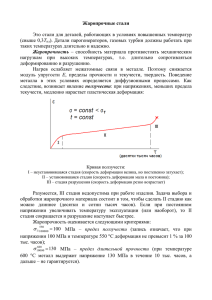
Лекция 16. Влияние времени нагружения и
среды на механические свойства материалов
Алгоритмы механических испытаний
№
Наименование
п.п испытания
.
Геометрия
образца
Вид
деформации
Программа
нагружения
Состояние
среды
Программа
измерений
1
На статическое
растяжение
Гладкий
цилиндрический
Растяжение
 = k.t
T = const
P = f()
2
На статическое
кручение
Гладкий
цилиндрический
Кручение
 = k.t
T = const
M = f()
На ползучесть
Гладкий
цилиндрический
Растяжение
P = const
4
На релаксацию
напряжений
Гладкий
цилиндрический
Растяжение
 = const
5
На длительную
прочность
Гладкий
цилиндрический
Растяжение
P = const
6
На усталость
(выносливость)
Гладкий
цилиндрический
Растяжение,
Изгиб
P=P0 sin(t)
T = const
7
На ударный
изгиб
Призматический
с надрезом
Изгиб
mgh0 = сonst
Txp<T<Tпл
Aр = mg(h0 – hк)
T = const
3
T> Tкомн.
 = f(t)
T = const
T> Tкомн.
P = f(t)
T = const
T> Tкомн.
tразр.= tк – t0
T = const
N=(/)( tк – t0)
Ползучесть
Ползучестью называют процесс медленного нарастания
остаточных пластических деформаций под действием постоянной
нагрузки
п
T > Tкомн
T = const
P = const
L0
T
0
Lп = f(t)
I
II
III
п = Lп/L0
 Lп
t
п = F(t) – кривая ползучести
P
I – стадия неустановившейся ползучести
II – стадия установившейся ползучести
III – стадия ускоренной ползучести
В упругом случае
0=P/EF
Влияние нагрузки и температуры на кривую
ползучести
п
P3
п
P2
T3
T1
P1



3
0
q
2
0
q
1
0
03
q
02
q
01
T = const
P = const
t
t
Р3 > P2 > P1
T2
T3 > T2 > T1
Пределы ползучести


Пределом ползучести  * называют напряжение, при котором
п
за данное время  деформация ползучести достигает заданного
*
значения п .
*
Критериальные значения  и п
определяются
техническими условиями на изделие. Например
час
  *   11000
%
п
В частности, значение  равно 300 часов для авиационных турбин
и свыше 100000 часов для турбин ТЭС и АЭС.

Пределом ползучести

 называют такое напряжение, при

котором минимальная скорость ползучести равна значению
устанавливаемому техническими условиями.
,
Расчет на ползучесть
Кривую ползучести заменяют прямой, наклон которой
совпадает с наклоном кривой ползучести на второй стадии.
Считают, что

 п  const
п
0
I
II
III
t
Тогда для любого момента времени можно дать оценку
деформации ползучести

 п t    п t   0
Расчет на ползучесть (продолжение)

m
Экспериментально установлено, что  п  A , где А и
m постоянные, определяемые для данного материала опытным путем.
 п 
1. Если предельно допустимая деформации ползучести
известна, то критерий прочности
A m t   0   п 
 п t    п 
или
откуда получаем допустимый временной ресурс работы изделия
1
t   п    0 
.
A m
  
2. Если известна предельно допустимая скорость ползучести п  ,
 
то

 
m
расчетное уравнение будет иметь вид  п  A   п 


1

  m
  п  


 




и получаем допустимое рабочее напряжение
A






.
Релаксация напряжений
Релаксация напряжений – это явление снижения напряжений в
нагруженной детали, полная деформация которой остается
постоянной.
Допустим, что стержень, имеющий длину L, растянут на
и жестко закреплен в этом состоянии.
L
0
L
  y   п  const
L
d y d п



0
 y  п
dt
dt


L
L

0
0 = const
 = const
п
T = const
y
t
t
Релаксация напряжений – это одно из проявлений явления
ползучести в условиях медленно изменяющихся напряжений.
Длительная прочность
Длительная прочность – сопротивление материала разрушению
при длительном статическом нагружении при повышенных
температурах.
lg(разр)
разр
T = const
T = const
I
разрi
II
tразрi
tразр
lg(tразр)
Область I - вязкое разрушение по телу зерна
(транскристаллитное разрушение);
Область II - хрупкое разрушение по границам зерен
(интеркристаллитное разрушение).
Предел длительной прочности
Предел длительной прочности – это напряжение  , при
котором разрушение происходит по истечении определенного
промежутка времени

при заданной температуре испытаний T .
Критерий длительной прочности имеет вид
   Д . П  ,
где
 Д .П   n ,
n
- коэффициент запаса.
Длительное циклическое нагружение
Усталость – процесс разрушения материала при
циклическом нагружении.
Выносливость – сопротивление материала усталостному

разрушению.
max
min
m
t
 р   max   min
 p  max   min
a 

Амплитуда цикла:
2
2
 max   min


m
Среднее напряжение цикла:
2
 min
r

Коэффициент асимметрии цикла:
 max
Размах напряжений цикла :
Испытания на усталость
P
Образец
Силовая плоскость

3
2

3
2

1
1
 = max Sin(t)
Нейтральная ось
Кривая усталости
Повторяя испытания для разных max , получают кривую
усталости – зависимость числа циклов до разрушения образца от
амплитуды циклических напряжений.
max
maxi
r = -1
Ni
N
Для черных металлов существует физический предел
усталости.
Предел усталости
Предел усталости (предел выносливости) – это
максимальное напряжение  r , при котором образец не
разрушится при любом числе циклов нагружения N . При этом
кривая усталости имеет асимптоту.
Для цветных металлов кривая усталости не выходит на
асимптоту. Для них определяют условный предел усталости –
напряжение  r, при котором образец выдерживает заданное чисто
8
циклов нагружения, например, N=10 .
Существует корреляция между пределом прочности
пределом усталости
r
:
Для сталей:
Для цветных металлов:
 r = (0,4 – 0,5)b;
 r = (0,25 – 0,5)b:
b
и
Диаграмма предельных циклов
a
-1
-1/n
N
i
a m

1
 1  T
T/n
T
b
m
a m 1


 1  T n
Ударные испытания
Направление удара P
10
10
40
m
H
h
Ударные испытания (продолжение 1)
Маятник поднимают на высоту H и он запасает
энергию
Aн = mgH.
Затем маятник падает, разрушает образец и поднимается
на высоту h .
Потенциальная энергия маятника после удара равна
Aк = mgh.
Работа А , которую затрачивает маятник на пластическую
деформацию и разрушение образца, равна
A = Aн – Aк = mg(H-h).
Удельную работу ударного разрушения образца (ударную
вязкость) определяют как
A
a ,
F
где
F
- площадь поперечного сечения образца в месте надреза.
Ударные испытания (продолжение 2)
Испытания проводят при различных температурах Т , что
позволяет построить кривую зависимости ударной вязкости
материала a от температуры испытаний Т измерить критическую
температуру хрупкости Txp :
a
-T
Txp
0
T
При температурах, которые меньше критической температуры
хрупкости, Т< Txp , материал становится хрупким.
Ударные испытания (схема Иоффе)

Сопротивление
отрыву
Сопротивление
срезу
Тхр
Т
Влияние среды на механические свойства
материалов
Влияние температуры среды
Влияние температуры среды (продолжение)
Коррозионное влияние среды
Коррозия – это разрушение материала, обусловленное
химическим взаимодействием металла с коррозионной средой.
Непосредственное химическое воздействие среды.
Электрохимическая коррозия.
Щелевая коррозия.
Эрозионно-коррозионный износ.
Межкристаллитная коррозия.
Коррозионное растрескивание под напряжением.
 Чистое железо в 50% аммонии (азотнокислый аммоний) имеет
длительную прочность в три раза меньше, чем на воздухе.
 Предел усталости стали ШХ-15 в кипящей воде в пять раз
ниже, чем на воздухе. Он падает с 850 МПа до 150 МПа.
 Коррозионный износ и последующий разрыв 500-мм
трубопровода второго контура АЭС Михама (Япония) создал
аварийную ситуацию, в результате которой на полгода были
остановлены 15 аналогичных блоков АЭС.
Влияние поверхностно-активных веществ
(Эффект Ребиндера)
Охрупчивание. Это резкое снижение пластичности и прочности под действием
жидкой среды, сходной с твердым телом по своей молекулярной природе. Для металлов
такими средами являются жидкие металлы иной группы.
Например, латунь и цинк становятся хрупкими в присутствии ртути.

Цинк на воздухе
Цинк с ртутью на поверхности

Влияние поверхностно-активных веществ
(Эффект Ребиндера) (продолжение)
Пластифицирование. Это снижение сопротивления пластической деформации
твердого тела в присутствии поверхностно-активного вещества.
Например, монокристалл олова в присутствии олеиновой кислоты в вазелиновом
масле существенно теряет сопротивление пластической деформации. Предел текучести
падает почти в три раза.

Олово на воздухе
Олово + 0,2 % олеиновой к-ты в
вазелиновом масле


02
Влияние нейтронного облучения на
статические механические свойства
материалов
При прочих равных условиях с ростом интегрального потока
(дозы) облучения (флуенса нейтронов) наблюдается
 Рост предел текучести 02
 Рост предела прочности (временного сопротивления) b
 Падение до нуля пластичности (относительного удлинения) 

b

02

Флуенс нейтронов
Влияние нейтронного облучения на скорость
ползучести
Присутствие нейтронного облучения приводит к увеличению
скорости ползучести в несколько раз. Например, на второй стадии
ползучести наблюдается следующее явление:

Облучение
При отсутствии облучения
t
02
Фотопластический эффект
. Освещение обычным светом некоторых твердых тел, например
сернистого кадмия (CdS) приводит к изменению диаграммы
статического деформирования.

Свет
Без света

02
Освещение приводит к усиленному перемещению электронов и,
поэтому, к торможению движения дислокаций и повышению
сопротивления пластическим деформациям.