Сегодня: суббота, 7 мая 2016 г. Ларионов В.В. Фазовые портреты

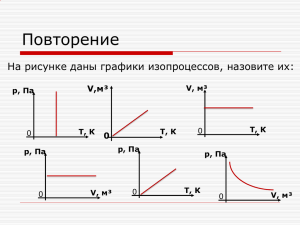
Сегодня: суббота, 7 мая 2016
г.
Ларионов В.В.
Фазовые портреты
Как изменяется характер движения
при изменении функции F(r,v)
Если сила постоянная, то решение обратной
задачи кинематики производят простейшим
образом. Из 2-го закона Ньютона ускорение
a = F/m, но a=dV/dt. Подставляя получаем,
dV=(F/m)dt, m = const. Интегрируем
v
t
F
dv

dt
v
0 m
0
F
v  v0  t
m
В векторном виде


 dr
 
   F
v
 dr  v dt  dr  (v  v0  t )dt
dt
m

Интегрирование уравнения по dr позволяет
найти изменение радиуса-вектора.
Если сила пропорциональна смещению
(например, сила упругости), то получаем
колебательное движение. Рассмотрим частный
случай одномерного движения, которое происходит
под действием квазиупругой силы F= -kx, где х –
изменение длины пружины (r=x).
Направление движения
F=-kx
m
x
Уравнение движения имеет следующий вид:
mx  kx
Так обозначено ускорение
Это однородное дифференциальное уравнение
2-го порядка.
k
2
x  x  x   0 x  0 0  k / m
m
Его решение известно из курса средней школы и
имеет вид (это уравнение колебательного
движения):
x  A cos(0t   )
А- амплитуда колебаний, ω0 - циклическая
частота, φ-начальная фаза.
ФАЗОВЫЙ ПОРТРЕТ
Итак смещение точки при колебательном
движении имеет вид:
x  A cos(0t   )
Найдем ее скорость
dx
v
 0 A sin( 0t   )
dt
И импульс p  mv  m0 A sin( 0t   )
Преобразуем уравнения в виде
x
 cos(0t   )
A
p
A0
  sin( 0t   )
Возведем в квадрат и сложим
x 2
p 2
( ) (
) 1
A
A0
Полученное уравнение – эллипс или окружность
носит название - фазовый портрет
колебательного движения частицы
P(x)
A0
x
A
Площадь эллипса равна равна произведению его
полуосей и можно доказать, что это
энергия Е колебательного движения за один
период, деленная на частоту   2 / 0
S   pdx 
E


- линейная частота колебаний
Фазовый портрет гармонических колебаний
Фазовый портрет при наличии затухания
Третий закон Ньютона
Третий закон утверждает: если тело 1
действует на тело 2 с силой F1, то в свою очередь
тело 1 обязательно действует на тело 2 с силой F2,
равной по величине и противоположной по знаку
силе F1; обе силы направлены вдоль одной прямой.
Третий закон отражает тот факт, что сила есть
результат взаимодействия двух различных тел.
F1
1
F2
2
3-ий закон говорит о том, откуда берется
сила во 2-ом законе
Закон сохранения импульса
Из 3-его закона Ньютона, как следствие,
можно получить закон сохранения импульса.
Пусть имеем замкнутую систему тел 1 и 2.
F1
1
F2
2
Запишем третий закон Ньютона.


F1   F2
С учетом 2-го закона, имеем:




dp1
d
p
2
 F1
 F2
dt
dt
Тогда:


dp1 dp2

0
dt
dt
Или
d  
( p1  p2 )  0
dt
Т.е. после интегрирования, получаем:
 
( p1  p2 )  const
В замкнутой системе двух тел их импульс есть
величина постоянная.
Этот результат может быть распространен на
любое число N тел
N

i 1

pi  const
Закон сохранения импульса
выполняется для замкнутой
системы тел. Система считается
замкнутой, если внешнее
воздействие отсутствует или мало
по сравнению с внутренними
силами.
Работа и энергия
Работой А называют интеграл от точки 1 по
криволинейной траектории до точки 2 (под
интегралом – векторы)
2
Fdr

А12=
2
1
1
F
Кинетическая энергия
Рассмотрим частицу массой m, на которую действует
некоторая сила F. Вычислим работу данной силы при
движении частицы (тела) по некоторой траектории от
1 до 2.
2
По определению А12=
Fdr

1
Fdr =
dp
dt
dr = m
dv
dt
dr = mvdv
но
dr/dt =v.
В классической механике m=const, т.е. массу можно
вынести за знак интеграла.
Этот интеграл равен
mV22/2 – mV12/2 =ΔEk
Из формулы
видно, что кинетическая
энергия зависит только от массы и
скорости тела, т.е. кинетическая энергия
есть функция состояния ее движения.
Кинетическая энергия в
релятивистском случае
Если масса зависит от скорости, то ее
величину нельзя вынести за знак
интеграла.
Преобразуем данную
формулу (т.е. возведем в квадрат и
раскроем скобки, введем импульс)
(1)
c2m2-p2 = m02c2 ,т.к. p= mv
Продифференцируем формулу (1)
2c2mdm – 2pdp =0. Сократим на 2.
c2mdm = pdp, или c2dm = pdp/m
Вычисляем работу, помня, что Fdr = mv
dv=p(dv m)/m= (p dp)/m.
Следовательно,
А12=
Получили элементарный интеграл,
который равен С2(m2 – m1). Если частица
стартовала с массой покоя m0 , то индекс 1
заменяем на 0, а m2 становится текущей, т.е
получаем С2(m – m0). Величина С2 m0 называется
энергией покоя.
Кинетическая энергия равна Ek = С2m - С2 m0.
Ek + m0 С2 = С2 m = E – полная энергия!!!
m0 – масса покоя частицы
Потенциальная энергия.
Консервативные силы
Есть силы, для которых выполняется условие
B
B
B
A
A
A
 F, d r    F, d r    F, d r 
Путь 1
Путь 2
Путь 3
Рис.
Рис.
Такие силы называют консервативными и
для сил, обладающих таким свойством, интеграл
называют потенциальной энергией и обозначают
буквой U:
U   F, dr 
Потенциальную энергию можно представить себе
как энергию, запасенную для дальнейшего
использования. Во многих случаях
ее можно
преобразовать в другие полезные формы энергии.
Закон сохранения импульса, наряду с законом
сохранения энергии, составляют систему двух
линейных уравнений и применяется для анализа
физических систем, когда учет всех сил затруднен.
Например, при соударениях частиц (шаров), при
расчете движения протонов в БАК (ЦЕРН,
Швейцария).
Сегодня: суббота, 7 мая 2016
г.
Лекция № 4
Момент силы
Моментом силы F относительно произвольной
оси называется векторное произведение радиусавектора r на вектор силы F. Радиус-вектор r и сила
F лежат в одной плоскости, перпендикулярной оси
вращения частицы m. M =[r,F] = - [F,r]
Вектор М направлен вдоль оси вращения по правилу
векторного
произведения
или
правилу
правого
буравчика. Скалярное значение момента силы равно M
=r F sin α
Схема векторов
z
M
β
r
F
α
Момент импульса
Понятие момента импульса вводится
аналогично понятию момента силы.
Моментом импульса L частицы массы m
называется векторное произведение
радиуса-вектора r на вектор импульса
частицы p L = [r,p] = - [p,r].
Вектор направлен по оси вращения по
правилу векторного произведения и
правилу правого буравчика. Его скаляр
равен
L=rpsin α
Схема векторов для определения момента импульса
Рассмотрим ось, произвольно ориентированную в пространстве, вокруг которой
вращается частица с импульсом Р.
z
Lz
L
β
r
P
α
Момент силы и момент импульса
связаны между собой
следующим образом
dL/dt = M
Если система замкнута, или силы действуют вдоль
оси, что также означает отсутствие момента силы,
то
dL/dt = 0 или L = const.
Мы доказали, что если на тело действует
центральная сила любого происхождения, или
система замкнута, то
момент импульса этого тела
будет сохраняться.
Для твердого тела момент импульса
вычисляется следующим образом
L=
I
I
- момент инерции твердого тела – аналог
массы для вращательного движения
I   r 2 dm
dm
r
Ось вращения
Моменты инерции некоторых тел
Материальной точки Диска -
1
I  mR 2
2
Шара - I 
2
mR 2
5
I  mr
2
Три фундаментальных закона механики
(закон сохранения импульса, энергии и
момента импульса имеют
общефизическое значение и
применяются во всех других областях
физики, включая атомную и ядерную)
Специальная теория
относительности
Механика
Ньютона
(называемая
также
классической) неверна при скоростях движения тел,
близких к скорости света
(v  с). Теория для
случая v  с называется релятивистской механикой
или специальной теорией относительности.
Классический закон сложения
скоростей по Галилею:
y
K
y’
K’
V0
x
x’
V0t
0
K
Частица м
K′
0’
Из простого сложения отрезков
находим X= X′ + V0t,
и взяв производную по времени получаем
′
x,x’
vx = v x + v0
Скорость света по формуле
Галилея равна сR = сV0,
т.е. может быть различной в
разных системах отсчета
Постулаты Эйнштейна:
1. Скорость света в вакууме постоянна во всех
инерциальных системах отсчета и не зависит от
скорости движения источника и наблюдателя.
2. Все инерциальные системы отсчета физически
эквивалентны
(принцип
относительности
Эйнштейна).
Закон сложения скоростей в теории
относительности (при больших
скоростях) имеет вид
Vx
v x  V

v xV
1
2
c
При малых скоростях (V<<c) этот закон
принимает вид классического закона
Галилея
Связь координат имеет вид
x
x   vt 
1 v / c
2
2
,
x 
x  vt
1 v / c
2
2
,
Сокращение длины по теории Эйнштейна
l  l0 1  β  l0
2
Замедление времени

T 
1  2
Тема: ПРИНЦИПЫ
СТАТИСТИЧЕСКОЙ МЕХАНИКИ.
РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА И
БОЛЬЦМАНА
В газах и жидкостях большое число
сталкивающихся атомов и молекул обуславливает
важные
закономерности
в
поведении
статистических переменных, не свойственные
отдельным атомам и молекулам.
Такие
закономерности
называются
вероятностными или статистическими.
Если
ограничиться
случаем
теплового
равновесия в физических системах, то мы будем
иметь дело со статистической
статистической механикой.
физикой
или
Статистическая
физика
позволяет
решить
принципиальные
вопросы,
связанные
с
описания
детализацией
большой совокупности атомов и молекул.
Это вопросы касаются распределения атомов
и молекул идеального газа по скоростям и по
энергиям, распределения атомов и молекул в
пространстве, где на них действуют силы, и от
точки к точке меняется их потенциальная
энергия.
Распределение молекул по скоростям.
Распределение Максвелла
Пусть у нас имеется N тождественных
атомных частиц, находящихся в состоянии
беспорядочного
теплового
движения
при
определенной температуре.
В результате каждого акта столкновения молекул
их скорости меняются случайным образом.
В процессе большого числа столкновений
устанавливается
стационарное
равновесное
состояние, когда число молекул в заданном
интервале скоростей сохраняется постоянным.
Функция распределения Максвелла F(v)
по абсолютным значениям скоростей
1 dN
 m 
F (v ) 
 4

N dv
 2kT 
3/ 2
mv 2

2
2 kT
v e
Позволяет определить долю молекул
dN
N
= F(v) Δv, имеющих скорости в интервале от v
до v + Δv
На рис. показана зависимость F(v) при различных
температурах.
Рис.
dN
N
Величина площадки под кривой – это доля
молекул, обладающих скоростями от v до v + Δv
Наиболее вероятная,
средне квадратичная и
средняя
арифметическая
скорости молекул газа
2kТ
υв 
m
Скорость, соответствующая
максимуму распределения
есть наиболее вероятная
скорость
– для
одной молекулы.
Средняя квадратичная скорость равна
3kТ
υкв 
m
Средняя арифметическая скорость
8kТ
υср 
m
Сегодня: суббота, 7 мая 2016
г.
Лекция № 5
Следствия из распределения
Максвелла
Из распределения Максвелла следует, что
средняя кинетическая энергия молекулы
массой m идеального газа равна
3kТ
υкв 
m
1 2
3
mυ кв  kT   
2
2
mυ
2
кв
 3kT
средняя кинетическая энергия
молекулы, состоящей из одного
атома
Если молекула состоит из 2 и более атомов, то энергия
равна
i
  kT
2
I - число степеней свободы, k-постоянная
Больцмана
Энергия моля (киломоля) газа
Чтобы получить полную кинетическую
(внутреннюю) энергию моля газа U надо
умножить среднюю энергию одной молекулы
на число молекул (например, число Авогадро)
N  6,02 10
23
1/моль
i
i
U  N  NkT  RT
2
2
R - универсальная газовая постоянная
Распределение Больцмана
Распределение
Больцмана
определяет
распределение частиц в силовом поле, в условиях
теплового равновесия
n(x) = n0exp[U(x)/kT].
Это
соотношение
называется
распределения
Больцмана
или
распределением Больцмана.
законом
просто
Условно это можно изобразить так:
Uk
U2
U1
В однородном поле тяжести, если перейти к
давлению, формула преобразуется к виду
P(x) = P0exp[gx/RT],
где   молярная масса газа, P0  давление
при x = 0 (например, на поверхности Земли).
Полученное
соотношение
носит
название барометрической формулы.
ИДЕАЛЬНЫЙ И РЕАЛЬНЫЙ ГАЗЫ
Идеальный газ
-радиус взаимодействия двух
молекул много меньше среднего
расстояния между ними, т.е
молекулы
взаимодействуют
только при столкновениях (рис.
1.1).
- объем всех молекул газа
много меньше объема,
занятого газом.
- потенциальная энергия взаимодействия молекул равна нулю
Реальный газ
радиус взаимодействия двух
молекул сравним с средним
расстоянием между ними,
т.е молекулы могут взаимодействовать не только
при столкновениях, но и на
некотором
расстоянии
между ними
– собственный объем молекул
газа может быть сравним с
объемом газа (сосуда.
Уравнения состояния для газов
Уравнение состояния
идеального газа
(Менделеева-Клапейрона)
( P )(V ) 
m

RT
Уравнение состояния
реального газа (Вандер-Ваальса)
a
( P  2 )(V  b)  RT
V
a, b – постоянные Ван-дер Ваальса, учитывающие взаимодействие и собственный объем молекул газа, соответственно.
Основное отличие состоит в следующем: 1)
количественное – по виду уравнений; 2)
качественное – состоит в том, что
реальный газ может быть сжижен,
идеальный газ перевести в жидкость нельзя.
ГЛАВНЫЕ СЛОВА:
Термодинамика
дает
полное
количественное
описание
обратимых
процессов. Для необратимых указывает
направление их протекания.
Первое начало термодинамики
Первое начало термодинамики есть закон
сохранения энергии для макроскопических
явлений, в которых одним из существенных
параметров, определяющих состояние тел,
является температура.
Закон сохранения энергии для систем,
в которых существенную роль играют
тепловые процессы, или первое
начало термодинамики записывается
в виде
Q = dU + A или Q = dU + PdV.
dU=CvdT; dQ=CpdT; dA = PdV
В формулах приняты следующие
обозначения: dU-изменение внутренней
энергии газа; Cv-теплоемкость газа
при постоянном объеме V, Cp –
теплоемкость газа при постоянном
давлении P. Теплоемкость- это
количество теплоты, необходимое для
нагревания одного моля газа на 1
градус.
dQ
С
dT
Циклы или круговые процессы
Цикл Карно (обратимый).
Никола Леонард Сади КАРНО –французский офицер
инженерных войск в 1824 г. показал, что работу
можно получить в случае, когда тепло переходит
от нагретого тела к более холодному (второе
начало термодинамики). Ввел понятие кругового и
обратимого процессов, идеального цикла тепловых
машин, заложил тем самым основы их теории.
Первое начало термодинамики не может
указать направление развития процесса.
Этот закон позволяет указать, как
изменяются термодинамические величины
в процессе.
Направление развития процессов
описывается вторым началом
термодинамики .
Цикл Карно
Идеальный цикл Карно состоит из 2-х
изотерм и 2-х адиабат. Газ получает
тепло Q1 при изотермическом
расширении (T1) и отдает Q2 при
изотермическом сжатии (но при более
низкой температуре T2).
Рис.
Для обратимого цикла Карно
ηобр
Т1  Т 2
Т2

 1 .
Т1
Т1
Для необратимого цикла
Т 2  ΔТ
Т2
ηнеобр  1 
 1 .
Т 1  ΔТ
Т1
Т.е всегда ηобр > ηнеобр – этот вывод справедлив
независимо от причин необратимости цикла Карно.
η – это коэффициент полезного действия
Термический коэффициент полезного действия
для кругового процесса
Q2
A Q1  Q2
η

 1
.
Q1
Q1
Q1
Все термодинамические процессы, в том числе и
круговые, делят на две группы: обратимые и
необратимые.
Процесс называют обратимым, если он
протекает таким образом, что после окончания
процесса он может быть проведен в обратном
направлении через все те же промежуточные
состояния, что и прямой процесс. После
проведения кругового обратимого процесса никаких
изменений в среде, окружающей систему, не
произойдет.
Процесс называется необратимым,
если он протекает так, что после его
окончания систему нельзя вернуть в
начальное
состояние
через
прежние
промежуточные
состояния.
Нельзя
осуществить необратимый круговой процесс,
чтобы нигде в окружающей среде не осталось
никаких изменений.
Например, обратимым можно считать процесс
адиабатического расширения или сжатия газа. При
адиабатическом
процессе
условие
теплоизолированности
системы
исключает
непосредственный теплообмен между системой и
Функция состояния, дифференциал которой dQ ,
T
называется – энтропией. dQ – элементарное
тепло, полученное (отданное) газом при
температуре газа Т
Энтропия обозначается S – это отношение
полученной или отданной теплоты к
температуре при которой произошла эта
отдача. С ее помощью определяют направление
процесса
dQ
 dS
T
Задание на дом
Найти изменение энтропии при переходе газа из
состояния T1V 1
в T2V2 (все величины
известны)
dQ
dS 
T
Q
P
T1
dQ
T2
RT
dQ  dU  PdV  CV dT  PdV  P 
V
S2
V1
V2
V
 dS  S
S1
2
 S1
Сегодня: суббота, 7 мая 2016 г.
Лекция № 6
Тема: Заряд и его
свойства, закон Кулона
КУЛОН Шарль Огюстен
(14.6.1736 – 23.8.1806) –
(Couloumb) французский
физик и военный инженер.
Сформулировал законы трения, качения и скольжения.
Установил законы упругого кручения. В 1725 г., построил
прибор для измерения силы – крутильные весы. В 1725
году Кулон открыл закон, названный в последствии его
именем. Раньше ожидали, этот закон должен быть похож
на закон всемирного тяготения. Так оно и оказалось,
только величина сил разная: если передать 1%
электронов от одного человека к другому, то сила
взаимодействия между ними на расстоянии вытянутой
руки будет больше веса земного шара. (Ранее крутильные
весы изобрел Кавендиш и на 10 лет раньше Кулона он
Макроскопические носители
зарядов. Кварки.
Заряженные частицы и ионы, q=1,6021892*10-19Кл.
mе = 9,1*10-31кг.
4πr2ρ
4πr2ρ
Нейтрон.
Протон.
0
0,5
r
1
Рис. 1.
1,5
r+dr
r,10-15м
0 0,5
1
1,5 r,10-15м
Рис. 2.
7