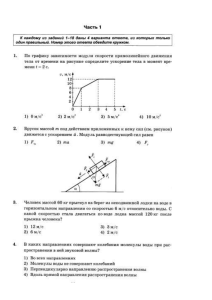
Пример 6. Трение качения

СТАТИКА
Трение качения
Пример
Цилиндрический каток 1 радиуса R и весом Q удерживается в
равновесии на наклонной плоскости, составляющей угол φ с
горизонтом, нитью, перекинутой через блок 2. К концу нити
подвешен груз 3 веса Р. Коэффициент трения качения fк.
Определить наибольшее и наименьшее значение веса груза Р, при
котором каток будет находиться в равновесии.
▼
1. Рассмотрим равновесие груза 3.
2. Активные силы, действующие на груз:
– вес груза 3.
Реакции внешних связей, действующие на груз:
– натяжение нити.
▼
3. Условие равновесия для плоской системы сходящихся
сил имеет следующий вид:
▼
4. Выберем систему координат.
x
5. Составим соответствующее уравнение равновесия в
аналитическом виде:
Следовательно,
Т = Р.
▼
Вычислим наименьшее значение силы Р (Рmin).
1. Рассмотрим равновесие цилиндрического катка 1.
2. Активные силы, действующие на каток:
– вес катка 1.
▼
Реакции внешних связей, действующие на каток:
– натяжение нити.
Причем
Т1 = Т = Рmin
▼
При наличии трения качения реакция представлена:
– нормальной реакцией поверхности;
– силой трения скольжения.
М
–
алгебраическим
препятствующей качению.
моментом
пары
сил,
▼
Реакция гладкой поверхности направлена по нормали к
этой поверхности.
М
А
Так как Р = Рmin, то возможное направление движения
катка – вниз по наклонной поверхности.
Следовательно,
Сила трения скольжения
наклонной поверхности.
направлена
вверх
по
▼
3. Выберем систему координат.
y
М
А
x
▼
4. Условие равновесия полученной произвольной
плоской системы сил записывается в виде:
y
М
А
x
(2)
(1)
(3)
▼
Для нахождения минимального значения силы Р
достаточно составить уравнение (3):
y
М
φ
А
Разложим силу
составляющие:
здесь
x
на две взаимно перпендикулярные
▼
Составим соответствующее уравнение равновесия:
y
М
А
x
▼
Так как
то
Откуда
▼
Вычислим наибольшее значение силы Р (Рmax).
1. Рассмотрим равновесие цилиндрического катка 1.
2. Активные силы, действующие на каток:
– вес катка 1.
▼
Реакции внешних связей, действующие на каток:
– натяжение нити.
Причем
Т1 = Т = Рmax
▼
Так как Р = Рmax, то возможное направление движения
катка – вверх по наклонной поверхности.
М
А
Следовательно,
Сила трения скольжения направлена вниз по наклонной
поверхности.
▼
3. Выберем систему координат.
x
М
А
y
Разложим силу
составляющие:
на две взаимно перпендикулярные
▼
Для нахождения максимального значения силы Р
достаточно составить уравнение моментов относительно
точки А:
x
М
А
y
▼
Так как
то
Откуда
▼
Таким образом
Если Р < Рmin, то каток катится вниз по наклонной
поверхности;
Если Рmin ≤ Р ≤ Рmax, то каток находится в равновесии;
Если Р > Рmax, то каток катится вверх по наклонной
поверхности.
▼