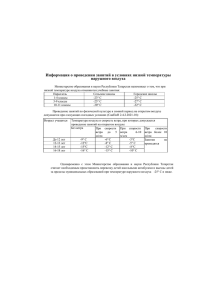
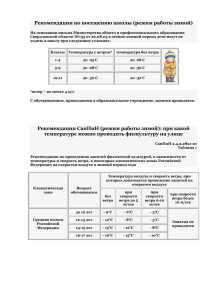
Пример флуктуаций магнитного поля

Особенности турбулентных
процессов в магнитосфере Земли
и плазме солнечного ветра
Л. В. Козак1, С. П. Савин2, А. Цупко1
1Киевский
Национальный Университет
имени Тараса Шевченка, Киев, Украина,
2ИКИ РАН, Москва, Россия
Схематическое изображение
магнитосферы Земли
Использованные данные
Для исследования
турбулентных процессов в
магнитосфере Земли
были использованы
данные измерений
магнитного поля проекта
Кластер-2 с частотой
опроса 22,5 Гц.
Шаг по времени
соответствует
t ~ 0.044-0.045 сек.
Рассмотренные в данной работе случаи:
1) 20 февраля 2005; 2) 20 февраля 2006; 3) 01 мая 2008;
4) 02 марта 2009.
Проанализированные значения магнитного поля
(20 Февраля 2005; 20 февраля 2006)
60
В, нТл
17:30 – 18:00 –
Магнитосфера (MP)
18:00 – 23: 10 –
Магнитослой (BS)
23:10 – 23:40 –
Солнечный ветер (SW)
40
20
t, сек
0
60000 65000 70000 75000 80000 85000 90000
80
В, нТл
60
40
20
t, сек
0
45000 50000 55000 60000 65000 70000 75000
13:30 – 14:00 –
Магнитосфера (MP)
14:00 – 19: 25 –
Магнитослой (BS)
19:25 – 19:55 –
Солнечный ветер (SW)
Проанализированные значения магнитного поля
(1 мая 2008; 2 марта 2009)
В, нТл
40
05:35 – 06:05 –
Солнечный ветер (SW)
06:05 – 15:10 –
Магнитослой (BS)
15:10 – 15:40 –
Магнитосфера (MP)
20
t, сек
0
20000
30000
40000
50000
60000
В, нТл
40
20
t, сек
0
0
5000
10000
15000
20000
25000
01:00 – 01:30 –
Солнечный ветер (SW)
01:30 – 06:15 –
Магнитослой (BS)
06:15 – 06:45 –
Магнитосфера (MP)
Пример флуктуаций магнитного поля
20 февраля 2006
80
1 мая 2008
В, нТл
В, нТл
20
60
40
Magnetopause
Magnetosheath
MP
SW
-
20
t, сек
49000
Tail Lobe
60
t, сек
0
0
49500
В, нТл
BS
20250 20500 20750 21000 21250 21500 21750
50000
40
В, нТл
BS
40
Solar
Wind
Plasma
Sheet
20
20
t, сек
0
0
51000 54000 57000 60000 63000 66000 69000
Tail Lobe
20
В, нТл
40
t, сек
25000 30000 35000 40000 45000 50000
В, нТл
SW
Ring
Current
Magnetosheath
MP
20
t, сек
0
0
69900 70200 70500 70800 71100 71400 71700
t, сек
55000
55500
56000
56500
Рассмотренные модели турбулентных процессов
1. Колмогоровская модель
2. Модель Ирошникова-Крейчнана
3. Лог-пуассоновская модель
Перемежаемость – это локальное нарушение однородности
турбулентности, в которой активные области сосуществуют с
квазиламинарными (Новиков и Стьюарт)
Статистический анализ
1. Анализ функции плотности вероятности
флуктуаций (PDF) магнитного поля
2. Рассмотрение эксцесса
3. ESS - анализ
Статистический анализ: PDF рассмотрение
Пример Гауссового
p ( x) 
 ( x  x0 )2 
1
exp  

2 2 
 2

и негаусового распределения
(распределение Леви)
p ( x,  ) 
1

exp( k

0

) cos kxdk
Пример эволюции негауссового
распределения с изменением шага
рассмотренных флуктуаций
P(0) ~ t-s ,
S ~ 0.5 – Гауссовое распределение
S > 0.5 – распределение Леви
Масштабные особенности PDF флуктуаций магнитного поля (2005)
Для исследования особенностей функции плотности вероятности флуктуаций магнитного поля выбирался
сдвиг по времени , кратный 0.0445 сек. Анализировались статистические свойства абсолютного значения
вариаций магнитного поля
10.00
P(dB)
dB  B (t   )  B (t )

10.0000 P(dB)




1.0000

1.00




10.000
P(dB)




1.000

0.1000
0.100
0.0100
0.10
0.010
0.0010
0.01
-5 -4 -3 -2 -1 0 1 2 3 4 5
dB, нТл
0.0001
-30 -20 -10 0 10 20 30
dB, нТл
0.001
-30-20-10 0 10 20 30
dB, нТл
Функции распределения плотности вероятности флуктуаций магнитного поля при различных сдвигах по времени
в период нахождения КА в плазме солнечного ветра (а), магнитослое (б) и во внутренней магнитосфере
100.00 P(0)
10.00
1.00
0.10
0.01
t,s
0.10
1.00
10.00
Зависимость
значения
максимума
функции
распределения
плотности
вероятности
флуктуаций магнитного поля P(0) от шага по
времени в логарифмическом
масштабе для
магнитослоя.
Экспериментальные
точки
-s
апроксимивались прямой P(0) ~ t . Для красной
линии s ~ 0. 83 для синей s ~ 0.48.
Масштабные особенности PDF флуктуаций магнитного поля (2006)
10.000
10.0000 P(dB)
P(dB)



1.0000



0.0
0.5
1.0


1.000


0.100
0.0100
0.010
P(dB)

0.1000
0.100
0.001
-1.0 -0.5
10.000


1.000


0.0010
0.010
0.0001
-40-30-20-10 0 10 20 30 40
0.001
dB, нТл
dB, нТл
-30-20-10 0 10 20 30
dB, нТл
Функции распределения плотности вероятности флуктуаций магнитного поля при различных сдвигах по времени
в период нахождения КА в плазме солнечного ветра (а), середине магнитослоя (б) и во внутренней магнитосфере
10.00 P(0)
1.00
0.10
t,s
0.01
0.01
0.10
1.00
10.00
Зависимость
значения
максимума
функции
распределения
плотности
вероятности
флуктуаций магнитного поля P(0) от шага по
времени в логарифмическом
масштабе для
внутренней магнитосферы. Экспериментальные
точки апроксимивались прямой P(0) ~ t-s . Для синей
линии s ~ 0. 81 для красной s ~ 0.44.
Масштабные особенности PDF флуктуаций магнитного поля (2008)
10.000
10.0000 P(dB)
P(dB)





1.0000


1.000
10.000


0.1000
0.0100
0.100
0.010
0.0010
0.010
0.001
-2
0.0001
0.100
0
-20
2
0
20
dB, нТл
dB, нТл


1.000

P(dB)

0.001
-20


0
20
dB, нТл
Функции распределения плотности вероятности флуктуаций магнитного поля при различных сдвигах по времени
в период нахождения КА в плазме солнечного ветра (а), форшоковой области (б) и во внутренней магнитосфере
100.00 P(0)
10.00
1.00
0.10
0.01
0.01
t,s
0.10
1.00
10.00
Зависимость
значения
максимума
функции
распределения
плотности
вероятности
флуктуаций магнитного поля P(0) от шага по
времени в логарифмическом масштабе для плазмы
солнечного ветра. Экспериментальные точки
апроксимивались прямой P(0) ~ t-s . Для красной
линии s ~ 0. 56 для синей s ~ 0.5.
Масштабные особенности PDF флуктуаций магнитного поля (2009)
10.0000 P(dB)

10.0000 P(dB)

10.00
P(dB)



1.0000



1.00

1.0000






0.1000
0.1000
0.0100
0.0100
0.0010
0.0010
0.0001
-40-30-20-10 0 10 20 30 40
0.0001
-30 -20 -10 0 10 20 30
0.10
0.01
-5 -4 -3 -2 -1 0 1 2 3 4 5
dB, нТл
dB, нТл
dB, нТл
Функции распределения плотности вероятности флуктуаций магнитного поля при различных сдвигах по времени
в период нахождения КА в плазме солнечного ветра (а), постшоковой области (б) и во внутренней магнитосфере
100.00 P(0)
10.00
1.00
0.10
0.01
t,s
0.10
1.00
10.00
Зависимость
значения
максимума
функции
распределения
плотности
вероятности
флуктуаций магнитного поля P(0) от шага по
времени в логарифмическом
масштабе для
постшоковой области ветра. Экспериментальные
точки апроксимивались прямой P(0) ~ t-s . Для
красной линии s ~ 0. 96 для синей s ~ 0.49.
Эксцесс
Эксцесс (kurtosis)
соотношением:
определяется
через

моменты
и
четвертого
порядка
S 4 ( )
 3,
( S 2 ( )) 2
где, S 4 ( )  X (t   )  X (t ) , S 2 ( )  X (t   )  X (t )  ,
X (t ) - исследуемый параметр.
4
второго
2
- масштабный параметр вариаций,
Для нормального распределения   0 .
Различают два типа возможных отклонений от нормального распределения:
 Одна из ниспадающих ветвей удлинена, распределение асимметрично. При этом, когда
удлинена левая ветвь, то имеем отрицательную асимметрию, а если удлинена правая
ветвь, то асимметрию называют положительной.
 Максимум расположенный выше или ниже, чем у нормального распределения. Если
максимум выше и кривая более остра – положительный эксцесс. При отрицательном
эксцессе максимум ниже и распределение более плоское.
Если значение эксцесса на разных временных масштабах остается постоянным, то это
указывает на отсутствие перемежаемости.
Значение эксцесса для флуктуаций модуля магнитного поля
(2005, 2006)
K
25
BS
100
K
BS
MP
MP
20
SW
SW
80
15
60
10
40
5
20
0
0
1
2
3
4
5
6
t, сек
Значение эксцесса для магнитослоя в
целом (синяя линия), внутренней
магнитосферы (красная линия) и плазмы
солнечного ветра (черная линия)
0
0
1
2
3
4
5
6
t, сек
Значение эксцесса для середины магнитослоя
(синяя линия), внутренней магнитосферы
(красная линия) и плазмы солнечного ветра
(черная линия)
Значение эксцесса для флуктуаций модуля магнитного поля
(2008, 2009)
15
K
BS
140 K
BS
MP
120
MP
SW
SW
100
10
80
60
5
40
20
0
0
1
2
3
4
5
6
t, сек
Значение эксцесса для форшоковой области
(синяя линия), внутренней магнитосферы
(красная линия) и плазмы солнечного ветра
(черная линия)
0
0
1
2
3
4
5
6
t, сек
Значение эксцесса для постшоковой области
(синяя линия), внутренней магнитосферы
(красная линия) и плазмы солнечного ветра
(черная линия)
ESS анализ
ESS (Extended Self-similarity) анализ - анализ особенностей структурных функций (моментов
функции плотности вероятности) разных порядков q в соответствии с временным интервалом.
Структурная функция определяется соотношением:
Sq ( )  X (t   )  X (t )
q
,
где ‹...› означает усреднение экспериментальных данных по времени.
При этом имеет место зависимость степени структурной функции от сдвига по времени :
S() ~ (q).
В случае полностью однородной изотропной Колмогоровской 3D турбулентности ζ(q) = q/3.
Для модели Ирошникова-Крейчнана - ζ(q) = q/4.
В лог-Пуассоновской турбулентной каскадной модели [В. Debrulle, 1994]:
q

3 1 
 (q)  (1  ) 
где

и
q


3 ,
1







– параметры, которые характеризуют перемежаемость и сингулярность диссипативных
процессов, соответственно. Для 3D изотропной турбулентности значение параметров     2 / 3.
q


q
 2 3 

 (q)   2 1    ,
 3 
9


ESS анализ заключается в определении относительного значения показателя экспоненты для разного
порядка структурных функций. В общем случае для q-го и р-го порядка существует соотношение:
Sq() ~ Sp() (q)/(p).
ESS-анализ для плазмы солнечного ветра, области
магнитопаузы и магнитослоя (2005)
4 q
3 q
K41
SL
MP
BS
3
2
2
1
IK
MP
BS
SW
1
q
0
0
1
2
3
4
5
6
7
8
9
Отношение
экспоненциального
значения
структурной функции q-того порядка к третьему
порядку. Крестиками отмечены экспериментальные
данные, прерывистая кривая соответствует значению
рассчитанному по формуле лог-Пуассоновской
каскадной модели (SL). Синяя линия соответствует
значению q/3 (модель Колмогорова К41).
0
0
1
2
3
4
5
6
7
8
q
9
Отношение
экспоненциального
значения
структурной
функции
q-того
порядка к
четвертому порядку. Синяя линия соответствует
значению q/4 – модель Ирошникова-Крейчнана
(IK)
max = 22; (=0.0445 сек).
ESS-анализ для плазмы солнечного ветра, внутренней
магнитосферы и середины магнитослоя (2006)
4 q
K41
SL
MP
BS1
SW
3
3 q
2
2
1
1
IK
MP
BS
SW
q
0
0
1
2
3
4
5
6
7
8
9
Отношение
экспоненциального
значения
структурной функции q-того порядка к третьему
порядку. Крестиками отмечены экспериментальные
данные, прерывистая кривая соответствует значению
рассчитанному по формуле лог-Пуассоновской
каскадной модели (SL). Синяя линия соответствует
значению q/3 (модель Колмогорова К41).
0
0
1
2
3
4
5
6
7
8
q
9
Отношение
экспоненциального
значения
структурной
функции
q-того
порядка к
четвертому порядку. Синяя линия соответствует
значению q/4 – модель Ирошникова-Крейчнана
(IK)
max = 22; (=0.0445 сек).
ESS-анализ для плазмы солнечного ветра, внутренней
магнитосферы и форшоковой области (2008)
4 q
3 q
K41
SL
MP
BS
3
2
2
1
IK
MP
BS
SW
1
q
0
0
1
2
3
4
5
6
7
8
9
Отношение
экспоненциального
значения
структурной функции q-того порядка к третьему
порядку. Крестиками отмечены экспериментальные
данные, прерывистая кривая соответствует значению
рассчитанному по формуле лог-Пуассоновской
каскадной модели (SL). Синяя линия соответствует
значению q/3 (модель Колмогорова К41).
0
0
1
2
3
4
5
6
7
8
q
9
Отношение
экспоненциального
значения
структурной
функции
q-того
порядка к
четвертому порядку. Синяя линия соответствует
значению q/4 – модель Ирошникова-Крейчнана
(IK)
max = 22; (=0.0445 сек).
ESS-анализ для плазмы солнечного ветра, внутренней
магнитосферы и постшоковой области (2009)
4 q
3 q
3
2
2
K41
SL
MP
BS
1
0
0
1
2
3
4
5
6
7
8
1
IK
MP
BS
SW
q
9
Отношение
экспоненциального
значения
структурной функции q-того порядка к третьему
порядку. Крестиками отмечены экспериментальные
данные, прерывистая кривая соответствует значению
рассчитанному по формуле лог-Пуассоновской
каскадной модели (SL). Синяя линия соответствует
значению q/3 (модель Колмогорова К41).
0
0
1
2
3
4
5
6
7
8
q
9
Отношение
экспоненциального
значения
структурной
функции
q-того
порядка к
четвертому порядку. Синяя линия соответствует
значению q/4 – модель Ирошникова-Крейчнана
(IK)
max = 22; (=0.0445 сек).
Определение диффузионных процессов
Обобщенный коэффициент диффузии, как функция от времени определяется
соотношением:
Df
  (1  1)   K
Для диффузии зависимость от времени отсутствует -K  0 ,
в случае супердиффузии K  0 , а при K  0 имеем субдиффузионный процесс.
Дата
Положение
ß
Δ
K
2005,
2006,
2008,
2009
Солнечный ветер
Модель Ирошникова-Крейчнана
2005
Магнитослой
Магнитосфера
0.53
0.26
1.10
0.12
0.98
0.35
2006
Середина магнитослоя
Магнитосфера
0.67
0.25
0.69
0.18
0.34
0.54
2008
Форшок
Магнитосфера
0.62
0.34
0.51
0.15
0.31
0.29
2009
Постшок
Магнитосфера
0.74
0.17
4.29
0.05
1.51
0.25
ВЫВОДЫ
При прохождении спутника через плазму спокойного солнечного ветра,
перемежаемость турбулентных процессов отсутствует.
Максимум функции
плотности вероятности Р(0) соответствует Гауссовому распределению.
Характер турбулентного течения плазмы в магнитослое не связан напрямую с
турбулентностью в солнечном ветре, и в значительной степени является
проявлением собственных процессов в данной области.
При анализе данных для магнитослоя и внутренней магнитосферы Земли мы
имеем на временном диапазоне до 1 сек (соответствует ионно-циклотронной
частоте) наличие перемежаемости процессов, а на больших временных масштабах
имеет место отсутствие перемежаемости (изменение максимума плотности
вероятности флуктуаций магнитного поля подобно типичному Гауссовому
распределению).
Турбулентные процессы в середине магнитослоя и в форшоковой области
описываются изотропной лог-Пуассоновской каскадной моделью; во всех других
рассмотренных случаях имеет место неизотропность процессов.
В магнитослое и во внутренней магнитосфере наблюдается супердифузия.
Наличие двух разных режимов указывает на два разных процессы: для описания
процессов с характерным временным масштабом более 1/fci можем использовать
уравнения магнитогидродинамики, а для описания процессов с малым
характерным масштабом – кинетические уравнения.
Спасибо за внимание!
General Remark on Turbulence
“It is trite to regard turbulence as the last unsolved problem in
classical physics and to cite many books and authorities to justify the
opinion. It is likewise a cliché to list great physicists and
mathematicians, such as Werner Heisenberg, Richard Feynman, and
Andrei Kolmogorov, who ‘failed’ to solve the problem despite much
effort. Horace Lamb and others have been credited with wishing to
seek heavenly wisdom on the subject when they arrived in heaven.
With such lists and stories, youngsters are cautioned, directly and
indirectly, that turbulence is beyond reasonable grasp.”
Gregory Falkovich and Katepali Sreenivasan
Physics Today, p. 43-49, April 2010.
Механизмы генерации колебаний в различных
структурных областях магнитослоя
Механизмы генерации колебаний в различных структурных
областях МС, по нашему мнению, различны.
В ФШ – генерация пучком отраженных
сформировавшимся при взаимодействии СВ c УВ.
ионов,
В ПШ – быстрая неустойчивость, имеющая взрывной
характер. Быстрому росту неустойчивых колебаний может
способствовать
высокий
уровень
затравочных
возмущений,
т.к.
амплитуда
колебаний
должна
увеличиться до ~4 раз при прохождении через УВ.
В МС - медленно раскачивающаяся, по-видимому,
кинетическая, неустойчивость за счет неравновесности
плазмы
МС.
Возбуждаемые
при
зеркальной
неустойчивости
колебания
представляют
собой
преимущественно волны сжатия поля (compressional
waves), волновой вектор которых должен быть
ориентирован почти поперек B.

Знаменитый Колмогоровский
закон для спектра потока энергии
равный 5/3
для модели ИрошниковаКрейчнана имеет место
соотношение 3/2
10
q=10
q=9
Log(S(q))
8
q=8
6
q=7
q=6
4
q=5
2
q=4
q=3
q=2
q=1.5
q=1
q=0.5
0
-2
-2.0 -1.0 0.0 1.0 2.0
Log(S(3))
Relative scales of q-th order structure function on 3-rd order structure function