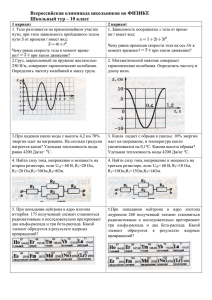
Гармонические функции

Дистанционный курс высшей математики НИЯУ МИФИ
Уравнения математической физики
6 семестр
Лекция 1
Гармонические функции 1.
17 марта 2014 года
Лектор: профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
Гармонические функции
xn
x  ( x1 , x2 ,..., xn )

| x | x12  x22  ...  xn2
  граница области 

x2


   x  { 1 , 2 ,..., n }, |  | 1
 2u  2u
 2u
u  2  2  ...  2
x1 x2
xn
x1
Уравнение Лапласа
u  0
Классические решения
u  C 2 ( ) C ( )
Гладкие решения
u  C 2 ( )
Гармонические функции
Гармоническая функция:
1) u  C 2 ()
2) u  0 в 
Формулы Грина
 v udx 

v

u
dS   (u, v )dx


v 
 u
 v u  uv  dx    v   u   dS
u
2
u

udx

u
dS

|

u
|
dx

 

u
 v  dS   (u, v )dx
u
  dS  0
v 
 u
  v   u   dS  0
u
2
u
dS

|

u
|
dx
 

Гармонические функции
Основные краевые задачи
Внутренние задачи (область Ω ограничена):
Дирихле:
Неймана:
 u( x )  0, x 

u( x )   ( x ), x 
 u ( x )  0, x  

 u ( x )
    ( x ), x  
Необходимое условие разрешимости
внутренней задачи Неймана:
  ( x )dS  0

Гармонические функции
Внешние задачи (область Ω является внешностью некоторой
ограниченной области):
Дирихле:
Неймана:
 u( x )  0, x 

u( x )   ( x ), x 
 u ( x )  0, x  

 u ( x )
    ( x ), x  
Дополнительное условие:
n=2 функция u(x) ограничена
n>2 функция u(x) имеет предел на бесконечности, равный нулю
Гармонические функции
Фундаментальное решение уравнения Лапласа
 1
n2
  2 ln | x |,
E ( x)  
1

, n2
n 2
 (n  2) n | x |
2 n /2
 n   dS 
(n / 2)
|x|1
1
n  3  E ( x) 
4 | x |
E ( x, y )  E ( x  y )
E ( x, y )  E ( y , x ), E ( x )  0,  x E ( x, y )  0,  y E ( x, y )  0
Гармонические функции
Интегральное представление функции класса C2.
yn


x
y1
y

  ограниченная область в R n ,
x , u( x )  C 2 ()
y2

u( y )
E ( x, y ) 
u( x )    E ( x, y )
 u( y )
dS y   E ( x, y ) u ( y )dy


 y
 y 
 

Гармонические функции
B( x,  )  { y  R n :| y  x |  }

S ( x,  )  { y  R n :| y  x |  }
y
u( y )
v ( y )  E ( x, y )
x
y

  E ( x, y )u( y )  u( y )E ( x, y ) dy 
   \ B( x,  )


u( y )
E ( x, y ) 
   E ( x, y )
 u( y )
 dS y

 y
 y 
 
Гармонические функции
  E ( x, y)u( y )  u( y)E ( x, y ) dy   E ( x, y )u( y )dy

0


u ( y )
E ( x, y ) 
  E ( x, y )  y  u( y )  y  dS y 

 

u ( y )
E ( x, y ) 
   E ( x, y )
 u( y )
dS y 


 y
 y 
 

u( y )
E ( x, y ) 
   E ( x, y )
 u( y )
 dS y

 y
 y 
S ( x , ) 
Гармонические функции

u( y )
E ( x, y ) 
 E ( x, y )u( y )dy    E ( x, y )  y  u( y )  y  dS y 




u( y )
E ( x, y ) 
   E ( x, y )
 u( y )
 dS y

 y
 y 
S ( x , ) 
x  S ( x,  )  | x  y | 
 1
n2
  2 ln  ,
E ( x, y )  
1

, n2
n 2
 (n  2) n
Гармонические функции
y 
r | y  x |


x  S ( x,  ) 

 y r
x
 1
n2
  2 ln r,
E ( x, y )  
1

, n2
n 2
 ( n  2) n r
 1

,

E ( x, y )  2 r

1
 y

,
n 1
  n r

n  2
1
1


 
n 1
n 1

r


n
n
n  2

Гармонические функции

u( y )
E ( x, y ) 
 E ( x, y )u( y )dy    E ( x, y )  y  u( y )  y  dS y 



 1


ln

,
n

2
 2
 u( y )
1

dS y 
u( y )dS y

n 1


1
 y
 n S ( x , )



,
n

2
n 2
(
n

2)




n
lim  E ( x, y )u( y )dy   E ( x, y )u( y )dy
 0


Гармонические функции
u  C 2 () 
u
u
 C (  )   M  0 y  S ( x ,  )
M
 y
 y
u( y )
u ( y )
n 1
dS

dS

M
dS

M


n
  y y   y y  y
 1

 M | ln  |


ln

,
n

2
2

,
n

2
 2
 u( y )
 2

dS y  



1
M
 y
n 1




,
n

2


, n  2
n
n 2
n 2
 ( n  2) n

 ( n  2) n

 M  | ln  |, n  2 


  M
0
n  2
 ( n  2) ,


(  0)
Гармонические функции
1
 n
n 1
  u( y )dS
y
 u(ξ), ξ  S ( x,  )
S ( x, )
ξ  S ( x,  )  | ξ  x |   ξ  x (  0)
u(ξ)  u( x ) (  0)
1
 n
n 1
  u( y )dS
y
 u ( x ) (  0)
S ( x, )

u( y )
E ( x, y ) 
 E ( x, y )u( y )dy    E ( x, y )  y  u( y )  y  dS y  u( x )



u( y )
E ( x, y ) 
u( x )    E ( x, y )
 u( y )
 dS y   E ( x, y ) u( y )dy

 y
 y 
 

Гармонические функции
Интегральное представление гладкой гармонической функции.
yn


x
y1
y
  ограниченная область в R n ,

x , u( x )  C 2 (), u( x)  0 ( x )
y2

u( y )
E ( x, y ) 
u( x )    E ( x, y )
 u( y )
dS y


 y
 y 
 
Гармонические функции
Теоремы о среднем.
xn
R
a
S
u(x) – гладкая гармоническая функция в B
B
x2
x1 S  {x :| x  a | R}
B  {x :| x  a | R}
 n /2
1
u(a ) 
u( x )dS x
n 1 
nR S
1
u(a ) 
u( x )dx
n 
n R B
2 n /2
n
n   dx 


 n
n n
|x|1
  1   n  
 2
2
Гармонические функции

u( x)
E (a, x) 
u( a )    E ( a, x )
 u( x )
dS x
 x
 x 
S
 1
n2
  2 ln R,
E (a, x )  
1

, n2
n 2
 (n  2) n R
E ( a, x )
1

 x
 n R n 1
u( x )
1
u( a )  E ( a, x ) 
dS x 
u( x )dS x 
n 1 
 x
nR S
S
1

u( x )dS x
n 1 
nR S
 u( x )

dS x  0 

 S  x

Гармонические функции
n 1
dx  r dr dS |x a|r
n  2  dS  rd  dx  rdrd  drdS
n  3  dS  r 2 sin  d d  dx  r 2 sin  drd d  drdS
R
R
 1

1
1
1
n 1
u( x )dx 
dr  u( x )dS 
 r dr 
u ( x )dS  
n 
n 
n  n
n 1



n R B
n R 0 |x a|r
n R 0

r
n
|
x

a
|

r


n
1

u
(
a
)

u
(
a
)
R
 nu(a )
n 1
n 1
n
n


r
dr

r
dr



 u(a )
n  n
n 
n
n R 0
n R 0
n R
n
nn
R
R
Гармонические функции
Гармонические функции на прямой (n=1)
u ''( x )  0  u  Ax  B
u  Ax  B
a
u  Ax  B
b
x
a
b
x
u( x )  const  min{u(a ), u(b)}  u( x )  max{u(a ), u(b)}
Гармонические функции
Сильный принцип максимума
Если функция гармонична в ограниченной области Ω (область – это
открытое и связное множество) и не является постоянной, то она не
может принимать свои наибольшие и наименьшие значения в точках
области Ω:
min u( x )  u( x )  max u( x )
x
x
Лемма. Если функция гармонична в шаре
B( a, R )  {x  R n :| x  a | R}
и принимает свое наибольшее значение в центре шара, то она
постоянна.
Гармонические функции
f , g  C (), f  g , f  g 
 f ( x)dx   g ( x)dx


Доказательство от противного.
u( x )  const  x u( x )  u( a )
f ( x )  u( x ), g ( x )  u( a )

| x  a | R
u( x )dx 

u(a )dx  u(a )
| x  a | R

dx  u(a )  n R n
| x  a | R
1
u( x )dx  u(a )
n

n R |x a| R
u(a )  u(a )
Гармонические функции
M  max u( x ), u( a )  M , a  

B2
B1
B3

b
Bk
a
u(x) принимает максимум в шаре B1 в его центре ---> u(x)≡M в B1
центр шара B2 лежит в B1
u(x) принимает максимум в шаре B2 в его центре ---> u(x)≡M в B2
………………………………………………………………………………..
………………………………………………………………………………..
центр шара Bk лежит в Bk-1
u(x) принимает максимум в шаре Bk в его центре ---> u(x)≡M в Bk
u(b)= u(a)
Гармонические функции
Следствия:
Слабый принцип максимума
min u( x )  u( x )  max u( x )
x
x
Принцип максимума модуля
| u( x ) | max | u( x ) |
x
u( x )  max u( x)  max | u( x) |
x
x
u( x )  max  u( x )   max | u( x) |
x
x
Гармонические функции
Принципы максимума для внешних задач.
Контрпример:
  {x  R n :| x | 1}
u
1
( n  2)
n 2
|x|
min u ( x )  1
u( x ) 

1
|x|
u 1
|x|
  {x  R n :| x | 1}
1
( n  2)
n 2
|x|
max u ( x )  1
u( x )  

Гармонические функции
Принцип максимума модуля
в классе убывающих к нулю функций.
u( x )  C 2 () C (), u  0 в , lim u( x )  0
|x|
| u( x ) | sup | u( x ) |

 0
R  0 | x  x0 | R  | u( x ) | 
R x
0

R  
B( x0 , R)
| u( x0 ) | sup | u( x) |
R
Гармонические функции
| u( x0 ) | sup | u( x) |
R
2
R
x0
R  1
2 , 1  S ( x0 , R) , 2   B( x0 , R)
1
x  1 | u( x ) | 

x   2 | u( x ) | sup | u( x ) |



| u( x0 ) | max  ,sup | u( x ) |



  0  | u( x0 ) | max 0,sup | u( x) |  sup | u( x) |

| u( x0 ) | sup | u( x ) |


Гармонические функции
Принцип максимума на плоскости.
u( x )  C 2 () C (), u  0 в , u( x ) ограничена в  (  R 2 )
inf u( x )  u( x )  sup u( x )


u( x )  sup u( x )

R
r a
R

x0
x0  , a  ,
  , x0  B( a, R )
B(a, r )
R  
B(a, R )
M  sup u( x ), N  sup u( x )


Гармонические функции
M  sup u( x ), N  sup u( x )

R
2
1

r a
R
x0

|xa|
ln
r
v( x )  u( x )  M  2 N
R
ln
r
R  1
2
1  S ( x0 , R) , 2  
B( x0 , R)
x  1  v ( x )  u( x )  M  2 N  (u( x )  N )  ( N  (  M ))  0
x   2 | x  a | r  ln
|xa|
 0  v ( x )  (u( x )  M )  2 N
r
ln
|xa|
r
0
R
ln
r
Гармонические функции
v( x0 )  max{0, max v( x)}  0
R
u ( x0 )  M  2 N
ln
| x0  a |
r
0
R
ln
r
R    u( x0 )  M  0  u( x0 )  M  sup u( x )

x   u( x )  sup u( x )

inf u( x )  u( x )

u ( x )  sup  u ( x )    inf  u ( x ) 


u( x )  inf u( x )

Гармонические функции
Принцип максимума модуля на плоскости.
u( x )  C 2 () C (), u  0 в ,
u( x ) ограничена в  (  R 2 )
| u( x ) | sup | u( x ) |

u( x )  sup u( x )  sup | u( x) |


u( x )  sup  u( x )   sup | u( x ) |


Гармонические функции
Принцип максимума Жиро.

x0

Пусть функция u(x) гармонична в области Ω, не
постоянна и достигает максимума (минимума)
в точке x0, лежащей на границе области. Тогда
u
 u

( x0 )  0 
( x0 )  0 

 

Гармонические функции
 a  {1},  b  {1}
n 1
u
u
(a )  u '(a ),
(b)  u '(b)


a
a
u  Ax  B
b
A 0
u
(a )   A  0

u
( b)  A  0

u  Ax  B 
b
a
b
x
a
b
A 0
u
(a )   A  0

u
( b)  A  0

x
Гармонические функции
Единственность решения краевых задач
Внутренняя задача Дирихле (область Ω ограничена):
 u( x )  0, x 

u( x )   ( x ), x 
 u1 ( x )  0, x  

u1 ( x )   ( x ), x  
 u2 ( x )  0, x  

u2 ( x )   ( x ), x  
u  u1  u2
 u( x )  0, x 

u( x )  0, x 
| u( x ) | max | u( x ) |
x
u( x )  0  u1 ( x )  u2 ( x )
Гармонические функции
Внешняя задача Дирихле
(область Ω является внешностью некоторой ограниченной области):
 u( x )  0, x 

u( x )   ( x ), x 
 u1 ( x )  0, x  

u1 ( x )   ( x ), x  
 u2 ( x )  0, x  

u2 ( x )   ( x ), x  
u  u1  u2
Дополнительное условие:
n=2 функция u(x) ограничена
n>2 функция u(x) имеет предел
на бесконечности, равный нулю
 u( x )  0, x 

u( x )  0, x 
| u( x ) | sup | u( x ) |
x
u( x )  0  u1 ( x )  u2 ( x )
Гармонические функции
Внутренняя задача Неймана (область Ω ограничена):
 u ( x )  0, x  

 u ( x )
    ( x ), x  
 u1 ( x )  0, x  

u1 ( x )
    ( x ), x  
 u2 ( x )  0, x  

u2 ( x )
    ( x ), x  
u  u1  u2
 u( x )  0, x  

 u( x )
   0, x  
u( x )  const

u1 ( x )  u2 ( x )  const
Гармонические функции
Единственность гладкого решения
 u( x )  0, x  

 u( x )
   0, x  
u
2
u

udx

u
dS

|

u
|
dx 

 

u  0  u  const
2
|

u
|
dx  0


Гармонические функции
Единственность классического решения
 u( x )  0, x  

 u( x )
   0, x  
Доказательство от противного:
u  const
В силу принципа максимума решение достигает в некоторой точке
границы своего максимального значения, тогда в этой точке в силу
принципа максимума Жиро
(противоречие).
u
0

Гармонические функции
Внешняя задача Неймана
 u ( x )  0, x  

 u ( x )
    ( x ), x  
 u1 ( x )  0, x  

u1 ( x )
    ( x ), x  
 u2 ( x )  0, x  

u2 ( x )
    ( x ), x  
u  u1  u2
Дополнительное условие:
n=2 функция u(x) ограничена
n>2 функция u(x) имеет предел
на бесконечности, равный нулю
 u( x )  0, x  

 u( x )
   0, x  
u( x )  const

u1 ( x )  u2 ( x )  const
Гармонические функции
 u( x )  0, x  

 u( x )
   0, x  
| u( x ) | sup | u( x) |
x
Доказательство от противного:
u  const
В силу принципа максимума решение достигает в некоторой точке
границы своего максимального значения, тогда в этой точке в силу
принципа максимума Жиро
(противоречие).
u
0

Гармонические функции
Уточнение для n>2
функция u(x) имеет предел на бесконечности, равный нулю
u1 ( x)  u2 ( x)  const  const  0  u1 ( x)  u2 ( x)
При n=2 два решения одной внешней задачи Неймана
отличаются на константу. При n>2 решение внешней
задачи Неймана единственно.
Дистанционный курс высшей математики НИЯУ МИФИ
Уравнения математической физики.
Гармонические функции 1.
Лекция 1 завершена.
Спасибо за внимание!
Тема следующей лекции:
Гармонические функции 2.
Лекция состоится в понедельник 24 марта
В 10:00 по Московскому времени.