Основные результаты выполнения проекта

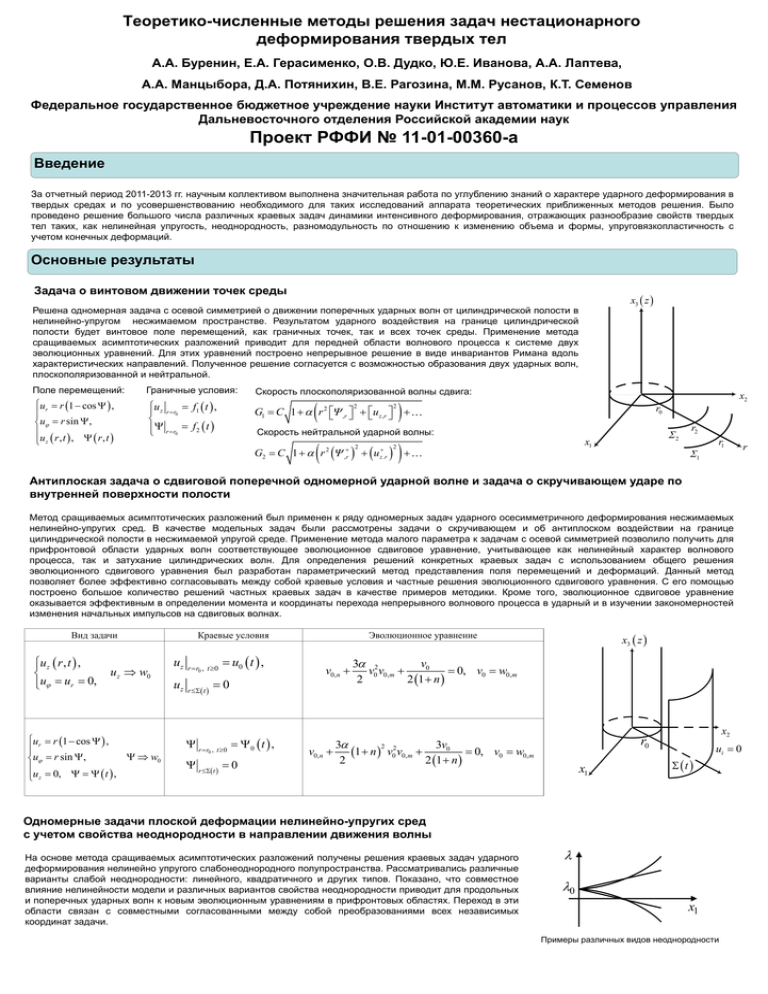
Теоретико-численные методы решения задач нестационарного
деформирования твердых тел
А.А. Буренин, Е.А. Герасименко, О.В. Дудко, Ю.Е. Иванова, А.А. Лаптева,
А.А. Манцыбора, Д.А. Потянихин, В.Е. Рагозина, М.М. Русанов, К.Т. Семенов
Федеральное государственное бюджетное учреждение науки Институт автоматики и процессов управления
Дальневосточного отделения Российской академии наук
Проект РФФИ № 11-01-00360-а
Введение
За отчетный период 2011-2013 гг. научным коллективом выполнена значительная работа по углублению знаний о характере ударного деформирования в
твердых средах и по усовершенствованию необходимого для таких исследований аппарата теоретических приближенных методов решения. Было
проведено решение большого числа различных краевых задач динамики интенсивного деформирования, отражающих разнообразие свойств твердых
тел таких, как нелинейная упругость, неоднородность, разномодульность по отношению к изменению объема и формы, упруговязкопластичность с
учетом конечных деформаций.
Основные результаты
Задача о винтовом движении точек среды
x3  z 
Решена одномерная задача с осевой симметрией о движении поперечных ударных волн от цилиндрической полости в
нелинейно-упругом несжимаемом пространстве. Результатом ударного воздействия на границе цилиндрической
полости будет винтовое поле перемещений, как граничных точек, так и всех точек среды. Применение метода
сращиваемых асимптотических разложений приводит для передней области волнового процесса к системе двух
эволюционных уравнений. Для этих уравнений построено непрерывное решение в виде инвариантов Римана вдоль
характеристических направлений. Полученное решение согласуется с возможностью образования двух ударных волн,
плоскополяризованной и нейтральной.
Поле перемещений:
Граничные условия:
ur  r 1  cos   ,

u  r sin  ,

u z  r , t  ,   r , t 
u z r  r  f1  t  ,
0

 r  r0  f 2  t 
Скорость плоскополяризованной волны сдвига:

2
2
x2

G1  C 1   r  ,r   uz ,r  
2
r0
Скорость нейтральной ударной волны:

G2  C 1   r 
2
  u   
 2
,r
2
x1
 2
z .r
r2
1
r1
Антиплоская задача о сдвиговой поперечной одномерной ударной волне и задача о скручивающем ударе по
внутренней поверхности полости
Метод сращиваемых асимптотических разложений был применен к ряду одномерных задач ударного осесимметричного деформирования несжимаемых
нелинейно-упругих сред. В качестве модельных задач были рассмотрены задачи о скручивающем и об антиплоском воздействии на границе
цилиндрической полости в несжимаемой упругой среде. Применение метода малого параметра к задачам с осевой симметрией позволило получить для
прифронтовой области ударных волн соответствующее эволюционное сдвиговое уравнение, учитывающее как нелинейный характер волнового
процесса, так и затухание цилиндрических волн. Для определения решений конкретных краевых задач с использованием общего решения
эволюционного сдвигового уравнения был разработан параметрический метод представления поля перемещений и деформаций. Данный метод
позволяет более эффективно согласовывать между собой краевые условия и частные решения эволюционного сдвигового уравнения. С его помощью
построено большое количество решений частных краевых задач в качестве примеров методики. Кроме того, эволюционное сдвиговое уравнение
оказывается эффективным в определении момента и координаты перехода непрерывного волнового процесса в ударный и в изучении закономерностей
изменения начальных импульсов на сдвиговых волнах.
Вид задачи
u z  r , t  ,

u  ur  0,
u z  w0
ur  r 1  cos   ,

  w0
u  r sin ,

u

0,



t
,


z

Краевые условия
uz
uz
r  r0 , t  0
r  t 
 u0  t  ,
0
 r  r , t 0   0  t  ,
0
 r t   0
Эволюционное уравнение
x3  z 
v0
3 2
v0,n 
v0 v0,m 
 0, v0  w0,m
2
2 1  n 
x2
r0
3v0
3
2 2
v0,n 
 0, v0  w0,m
1  n  v0 v0,m 
2
2 1  n 
x1
 t 
ui  0
Одномерные задачи плоской деформации нелинейно-упругих сред
с учетом свойства неоднородности в направлении движения волны
На основе метода сращиваемых асимптотических разложений получены решения краевых задач ударного
деформирования нелинейно упругого слабонеоднородного полупространства. Рассматривались различные
варианты слабой неоднородности: линейного, квадратичного и других типов. Показано, что совместное
влияние нелинейности модели и различных вариантов свойства неоднородности приводит для продольных
и поперечных ударных волн к новым эволюционным уравнениям в прифронтовых областях. Переход в эти
области связан с совместными согласованными между собой преобразованиями всех независимых
координат задачи.

0
x1
Примеры различных видов неоднородности
r
Многомерная задача ударного деформирования нелинейно-упругой среды
Представлено обобщение метода построения приближенных решений краевых задач динамики ударного деформирования в виде лучевых разложений для
двумерных задач плоской деформации, в которых возникают два типа ударных волн: чисто продольная и квазипоперечная. Для каждой ударной волны в
окрестности ее волнового фронта решение определяется на основе лучевых координат, согласованных с данной волной. Учтена нелинейная расходимость
криволинейных лучей. Представлен принципиально важный для лучевого метода механизм преобразования одной лучевой координатной системы к другой.
Разработанные приемы иллюстрируются решением задачи об ударной деформации полупространства с границей ненулевой кривизны.
Распространение возмущений по несжимаемой упругой среде с разномодульным сопротивлением сдвигу
c u2,11  u2 ,
2




a  



п
ри
u

0,
1
2,1

2
c 
3 
2
1 1
b   3 1  2 2 п ри u2,1  0,


2  2  b  a.
2
1
1
3
3
2

2
Кусочно-линейное уравнение движения несжимаемой
разномодульной
упругой
среды
с
различным
сопротивлением сдвигу вдоль выбранной оси x2
(t),
L
x1
'(t)
u2(x1,t),
u2,1
t2
t1
0
t
0
t1
x1
o
c
=
u2(x1,t),
u2,1
t
s
n
s 21
t1
t2
d
(в)
(t),
'(t)
x1

t
(б)
(а)
0
b
G
0
Изучены
особенности
распространения
граничных
возмущений в разномодульной несжимаемой упругой
среде,
по-разному
сопротивляющейся
сдвиговым
нагрузкам,
приложенным
в
противоположных
направлениях. Для случая плоских волн решены
одномерные краевые задачи об ударном сдвиге на границе
полупространства. Показано, что обобщенное решение
одномерного квазилинейного уравнения движения в случае
одноосного деформирования разномодульной среды при
последовательном изменении направления приложенных
граничных нагрузок может содержать нелинейные
эффекты: сильные разрывы первых производных
перемещений (ударные волны, движущиеся слои
постоянных перемещений (жесткие области).
b
a
a
0
x1
t
0
(г)
t
t1
(д)
g2 g1
d
(е)
Возникновение
ударной
волны
сдвиговой
нагрузки

и
движущегося
недеформированного слоя [g1;g2] при одномерном ударном деформировании
несжимаемого упругого полупространства с разномодульным сопротивлением сдвигу
вдоль оси x2: (а), (г) – заданная функция перемещений u2=f (x1,t) на границе
полупространства; (б), (д) – характеристические плоскости после момента смены знака
граничной нагрузки; (в), (д) – перемещения u2(x1,t) и деформации u2,1 после смены
направления сдвига на границе полупространства.
Автомодельная задача о динамике разгрузки упругопластического полупространства
Поставлена и решена плоская автомодельная задача о ступенчатом,
высокоскоростном
снятии
нагружающих
усилий
с
границы
упругопластического
полупространства
со
значительным
уровнем
накопленных необратимых деформаций. В результате разгрузки по среде
начнут распространяться возмущения, которые в данной постановке могут
распространяться либо посредством ударных волн, либо посредством
простых волн, известных также как волны Римана. Поскольку мы имеем дело
с разгрузкой, то согласно термодинамике, первой будет распространяться
простая волна Римана (несущая собой основные изменения объемных
деформаций). В отношении второй волны до момента решения конкретной
краевой задачи нельзя точно сказать, какого она будет типа. Однозначность в
совокупности возникающих волн разгрузки (простые волны или плоские
разрывы)
основывается на
законах
термодинамики
и
условиях
эволюционности распространяющихся разрывов деформаций.
Задача о распространении волны разгрузки в тяжелом слое при продолжающемся вязкопластическом течении
Огромный вред экономике, который несут стихийные бедствия, такие, как сход снежной лавины и
землетрясения, обуславливает необходимость математического моделирования возникающих
возмущений в процессе перехода от трения покоя к трению скольжения. Т.к. массивы, считающиеся
разрушительными, исчисляется в десятках тысяч тонн, то необходимость использования модели больших
упруговязкопластических деформаций неоспорима. Важной особенностью является то, что
распространения возмущения происходит от опорной поверхности, в то время как с другой стороны
продолжается давление, таким образом, упругая волна разгрузки, возникающая при срыве слоя с опоры,
будет распространяться по области продолжающегося вязкопластического течения. В рамках теории
больших упругопластических деформаций построено аналитическое решение, описывающее возмущение
в каждый момент времени.
1
1
dij  (ui , j  u j ,i  uk ,i uk , j )  eij  pij  eik ekj  eik pkj  pik ekj  eik pkmemj
2
2
Основные публикации
1. Буренин А.А., Ковтанюк Л.В. Упругие эффекты при интенсивном необратимом деформировании: монография. Владивосток: ДВГТУ, 2011. 280 с.
2. Рагозина В.Е., Иванова Ю.Е. Эволюционное уравнение для одномерных сдвиговых волн разрыва деформаций // Вестник СамГУ. Естественнонаучная серия. Механика. Самара: Изд-во "Самарский университет", 2011. № 2(83). С.
91-104.
3. Рагозина В.Е., Иванова Ю.Е. Метод возмущений в одномерной динамике несжимаемых упругих сред при ударных воздействиях // Вестник Нижегородского университета им. Н.И. Лобачевского. Н. Новгород: Изд-во ННГУ им. Н.И.
Лобачевского, 2011. №. 4. Ч. 5. С. 2192-2194.
4. Буренин А.А., Ковтанюк Л.В., Кулаева Д.В. О взаимодействии одномерной волны разгрузки с упругопластической границей при ее распространении в упруговязкопластической среде // ПМТФ. Новосибирск: СО РАН, 2012. Т. 53.
№1. C. 105-113.
5. Burenin A.A., Kovtanyuk L.V., Kulaeva D.V. Interaction of a one-dimensional unloading wave with an elastoplastic boundary in an elastoviscoplastic medium // Journal of Applied Mechanics and Technical Physics. Springer New York, 2012. Vol.
53. No. 1. P. 90-97.
6. Рагозина В.Е., Иванова Ю.Е. Математическая модель движения сдвиговых ударных волн ненулевой кривизны на основе их эволюционного уравнения // Сибирский журнал индустриальной математики. Новосибирск: Изд-во
Институт математики им. С.Л. Соболева СО РАН. 2012. Т. 15. № 1(49). С. 77-85.
7. Рагозина В.Е., Иванова Ю.Е. Эволюционное уравнение плоских ударных волн в несжимаемых средах со слабой неоднородностью // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева.
Серия: Механика предельного состояния. Чебоксары: Изд-во ЧГПУ, 2012. №4 (14). С. 95-104.
8. Рагозина В.Е., Иванова Ю. Е. Эволюционное уравнение поперечных ударных волн в твердом теле // Дальневосточный математический журнал. Владивосток: Дальнаука, 2013. Т. 13, №1. С. 116-126.
9. Рагозина В.Е., Иванова Ю.Е. Влияние неоднородности среды на эволюционные уравнения плоских ударных волн // ПМТФ. Новосибирск: Изд-во СО РАН, 2013. Т. 54, № 5. С. 142-153.
10. Дудко О.В., Лаптева А.А. К распространению возмущений по несжимаемой упругой среде с разномодульным сопротивлением сдвигу // Сибирский журнал индустриальной математики. Январь-март, 2013. Т. XVI, № 1(53). С. 21 28.
11. Манцыбора А.А., Русанов М.М. Автомодельная задача о динамике разгрузки упругопластического полупространства //Сиб. журн. индустр. матем. 16:2 (2013). С. 122–129. 12. Ivanova Yulia, Ragozina Victoria The evolutionary
equation for wave processes of the shift deformation // Applied Mechanics and Materials. Vols. 249-250 (2013). PP. 132-136.
13. Ragozina V.E., Ivanova Yu.E. Effect of the medium inhomogeneity on the evolution equation of plane shock waves // Journal of Applied Mechanics and Technical Physics. Springer New York, 2013. Vol. 54. No. 5. P. 809-818.
14. Рагозина В.Е., Иванова Ю.Е. Эволюционные уравнения как метод изучения динамики деформирования упругих неоднородных сред // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева.
Серия: Механика предельного состояния. Чебоксары: Изд-во ЧГПУ, 2013. №2 (16). С. 87-97.