Характеристики вращательного движения атмосферы

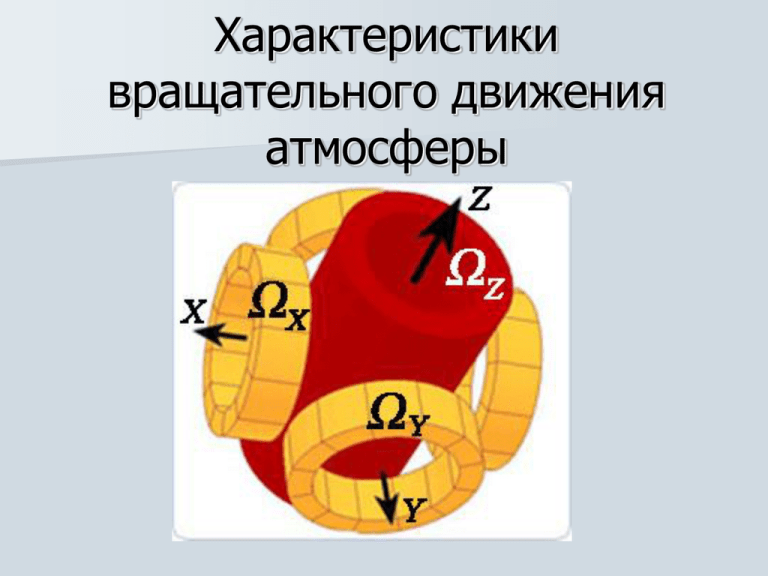
Характеристики
вращательного движения
атмосферы
Вихрь (относительный, переносный,
абсолютный и потенциальный)
используется для описания
вращения
в горизонтальной плоскости
Это знаменитый норвежский Мальстрём
Зачем нам нужен вихрь?


Для ответа
следует
выяснить, как
образуются
вертикальные
токи в
атмосфере.
Вспомним
геострофическое
приближение
В геострофической атмосфере
вертикальных токов быть не может!
Докажем это
Вертикальные токи в атмосфере определяются с помощью уравнения
неразрывности. Оно для атмосферы имеет вид:
 u v 
 w
  
 
z
 x y 
Для территорий примерно 1000Х1000 км горизонтальные изменения
плотности и параметра Кориолиса пренебрежимо малы. Поэтому
дивергенция геострофического ветра может быть вычислена так:
 ug vg    1 p    1 p  1   p  p 

 

 

 
0

 x

y
x   l y  y   l x   l  x y y x 


Откуда следует:
 ug v g 
   w()  0
 w( z )     

 x
y 
z


z 
Куда делись вертикальные токи?
Они исчезли вследствие предположения
о геострофичности.
 Если отказаться от этого
предположения, то придется добавить в
определение скорости ветра
агеострофическую поправку, т.е.
ускорения. Получим:

1 p 1 dv
1 dv
dv
1 p
u

u 
(это уравнение

 lu )
g
l  y  l dt
 l dt
dt
 y
1 p 1 du
1 du
du
1 p
v

v 
(это уравнение

 lv)
g
l  y  l dt
 l dt
dt
 y
Рассчитаем дивергенцию
агеострофического ветра,
пренебрегая пока изменениями
плотности
 u g vg
w
   U s  


z
x
y

   1 dv    1 du 
 

 x  l dt  y  l dt 

   1 dv  1 d  v  u v v v
 x  l dt   l dt  x   x x  x y

 
1  d  v u   u v   v u  
 

            
l  dt  x y   x y   x y  
   1 du   1 d  u   u u  v u
 y  l dt  l dt  y  y x y y
откуда следует, что
w
  1 dv    1 du  1  d  w
w
1 d

   U s  












z
x  l dt  y  l dt  l  dt
z
z  l    dt

Выводы о природе вертикальных токов в
атмосфере:



Вертикальные токи возникают в атмосфере вследствие
ее инерции (ускорений или агеострофичности ветра)
Но не просто ускорений, а из-за неоднородности поля
ускорений
Мерой неоднородности поля ускорений является
изменение в частице воздуха величины
 = дv/дx-дu/дy


Эта величина называется вертикальной составляющей
вектора вихря скорости движения атмосферы
Уравнение
дw/дz=-1/(+l)·d/dt
называется уравнением вихря.
Значит вертикальная скорость в атмосфере
рассчитывается с помощью уравнения вихря!
Для любознательных: как
формируется погода на завтра во
втором приближении
Из математики: векторное
произведение




Вектор C – векторное
произведение
На рисунке (правая тройка)
оно положительно
Направление движения – от
A к B (против часовой
стрелки) также должно
быть положительным
Именно поэтому вращение
против часовой стрелки
считается положительным
(Zn), а против отрицательным (Az)
Из математики : криволинейный интеграл
Определение
Способы вычисления: формула Грина

Pdx  Qdy 
(l )
 Q P 
  x  y  dxdy
( s)
B
B
B
A
A
A
F
F
 Pdx  Qdy   x dx  y dy   dF  F ( B)  F ( A)
Независимость от пути интегрирования: подынтегральное выражение –
полный дифференциал некоторой функции F
Циркуляция и дивергенция
V

dl

n
Если
проинтегрировать
по
контуру
нормальную
составляющую, то получим площадь, увеличения ( или
уменьшения)
контура
.
(Так
можно
оценивать
дивергенцию/конвергенцию)
Если проинтегрировать по контуру
касательную составляющую, то
получим
циркуляцию по контуру
С   V  dl   V cos(V, dl ) dl 
s
  udx  vdy  wdz
Смысл: циркуляция показывает в
какую сторону жидкость будет
вращать гребное колесо, в
интересующей нас части жидкости
Чтобы колесо вращалось
не обязательно,
Чтобы скорость на разных сторонах
контура была направлена в разные стороны
Циркуляция позволяет оценить угловой
момент для частиц жидкости.
Действительно: если взять
круговой контур и считать, что
жидкость обтекает его с
постоянной линейной
скоростью V=r , то получим
2
2
C   V  dl   r d 
2
0
 2  r  2  Vr  2  M
Внутреннее вращение в изолированной системе при
сохранении общего углового момента должно
изменять вращение остальных частей системы!
Пример: Если вращающееся колесо в руках
повернуть осью вниз, то человек будет вращаться в
противоположную сторону
Поэтому расчет циркуляции важен для метеорологических оценок
Математическое определение понятия
«вихрь скорости»

v 
u 

 C  u x   v   x    y   u   y    x  v y 
x 
y



 v u 
      x y  при  A= x y  0
 x y 
 v u 
C
существует предел  :

   
 x y
 x y 
Это предел-циркуляция по бесконечно малому контуруназывается «вихрем скорости»
Более строгое определение следует из теоремы Стокса:

V

dL



V

n
dA

rotV



lim


VdL
V
A
A0
Вихрь– это вектор, он имеет
три составляющие
Ω  rotV    V
i

Ω   i  j k 
x
y
z
x
u
j

y
v
k


z
w
 w v   w u 
 v u 
 i
   j
   k  

y

z

x
z 

 
 x y 
откуда следует, что
w v
u w
v u
 ,  

,   
y
z x y
y z
z x
 
x
 ,  - горизонтальные составляющие вихря
x
y
 - вертикальная составляющая вихря
z
Вертикальную составляющую вихря
обозначают так:
 v u 
      z  rotz Ω
 x y 
Интерпретация вихря с помощью
равномерного вращения
(+)
равномерное вращение по часовой стрелке
против часовой стрелки (-)
V(r)=  r помнить dr  dn R  r  0
тогда  
V V r


 () 
R n
r
  2
Вектор вихря по величине скорости
движения жидкости в точке равен удвоенной
угловой скорости вращения этой точки и
положителен, когда вращение происходит по
часовой стрелке
Вращения Земли и вихри: переносный,
относительный, абсолютный
Абсолютная геоцентрическая система координат
Относительная стандартная система
координат
Суммарная (абсолютная) циркуляция в
атмосфере Земли всегда есть сумма
локальной (относительной) циркуляции, и
переносной циркуляции, связанной с
Земли
Формула переносного вихря скорости,
создаваемого только вращением Земли
V  ω  r 
e
ω  k r x i  y  j  z k
i j k
тогда V  0 0   yi  xj
e
x y z
i
j


и rot V    V 
e
e
x y
y x
k

 2 k
z
0
Обратить внимание: все выкладки в абсолютной системе координат!
Заметка: в переводе с английского
переносный вихрь называют планетарным вихрем
Вихрь переносного движения. (2 способ)
Обратить внимание:
все выкладки в
абсолютной системе
координат!
C  2 S  2 S  sin 
e
z
C
rotV  lim e  2 sin 
e
S 0 S
2
O(rotV ) 
 104 c1 
e
 
24  3600
принятое обозначение rotV  f
e
Циркуляция переносного движения равна удвоенной угловой скорости
Земли, умноженной на проекцию площади контура на экваториальную
плоскость (см. предыдущую лекцию)
Контрольный вопрос: вычислить вихрь
скорости движения воздуха в точке
r(x,y)={1м,2м},если вектор скорости
задан в виде:V={u0·x·y,v0·y}. Причем
u0=2 мс-1, а v0=1 мс-1
 Контрольный вопрос: вычислить
абсолютный вихрь скорости движения
воздуха в точке r(x,y)={1м,2м},если
вектор скорости задан в
виде:V={u0·x·y,v0·y}. Причем u0=2 мс-1, а
v0=1 мс-1 , а широта места 300N

Что нужно помнить про вихрь

Вихрь – это вектор, связанный со скоростью соотношением :
rotV=V



Метеорологи обычно рассматривают движение на плоскости и
интересуются только вертикальной составляющей вихря
Размерность вихря – [rotV]=[дvдx]=[дuдy]=c-1
Порядок величины вертикальной составляющей вихря
скорости ветра в атмосфере
O(дvдx- дuдy)10-4c-1

На метеорологические карты наносятся значения
(rotV)·105, т.е. на картах O(дvдx- дuдy)10
 Переносный вихрь(f) положителен, он существенно
больше относительного (f>>), связанного с
собственным движением атмосферы.
 Поэтому вихрь суммарного движения - абсолютный
( ) близок к переносному ( = f +   f )
Вихрь в натуральных координатах:
касательная (s)-х, нормаль (n)- у
V


 n  s
n


d  s   n  
V
 C  V   s  V   n   V   s 
 n  s
n
  V 
 C  V 

  n  s
  s n 
 C  V   s  d  s    V 
  lim
 C   V
 V 

 S   s n
V

, где K 
- кривизна траектории
n
s
V V
1
  
, где R  - радиус кривизны траектории
R n
K
 V K 
или

 , где  S   n   s

иначе
Вывод уравнения абсолютного вихря из уравнений
движения с помощью векторных операций
dV
1
V
1
1

 g   p 
  V 2   Ω  V   g   p
dt

t

2

 V
 


t


1
1 2
 V   Ω V  g   p  

2


1

Ω
1 2
   V    ( Ω  V )      p 
t
2





1

1
1 2
    p  
  p 
   V   0 ,
2
2


 






(
Ω

V
)

Ω

div
V

V

div
Ω

Ω


V

V


Ω


dΩ
1
 Ω  divV   Ω  V 
  p
2
dt

Подробный вывод см. в лекции 12 учебника или курсах гидродинамики
Доказательство правильности
определения вихря с помощью
равномерного вращения
равномерное вращение вправо
V(r)=  r помнить dr  dn R  r  0
V V r
тогда   

 () 
R n
r
  2
Вектор вихря скорости движения жидкости в
точке равен удвоенной угловой скорости
вращения этой точки
Определение знака вихря по формуле:
 = V/R-дV/дn
Влияние кривизны
траектории
Влияние градиента
(сдвига) скорости
потока
ПОМНИТЬ: а) Радиус кривизны линии меняет знак (+ против час. стрелки)
б) нормаль направлена влево, если встать спиной к ветру
Контрольный вопрос:

Расставить
знаки вихря
скорости
относительног
о движения по
волнообразны
м траекториям
в северном
Вычисление вихря в изобарических
координатах
в изобарических коорд инатах
p
p
dZ 1 p
dp  0 
dn 
dZ  g


n
Z
dn  n
откуда
1 p 1 Z
1 p 1 Z
ug  

, vg 

 l y l y
 l x l x
поэтому
vg u g
  g Z    g Z  g 2
g 

 
  Z
  
x
y
x  l x  y  l y  l
Вычисление вихря по геострофическому ветру
(практика)
1 2
g   p

l
i, j
g 
4
 ld
g 
pср  pi, j  

2

4g
Zср  Zi, j
ld 2

Вывод формулы полезен для всех
pi 1, j  pi, j    pi, j  pi 1, j 


,
2 p
x 2
i, j
2 p
y 2
d2
pi, j 1  pi, j    pi, j  pi, j 1 


d2
i, j
1
4
g   2 p

2
l
i, j  ld
или
где
g 
 pi 1, j  pi, j 1  pi 1, j  pi, j 1

 pi, j 


4



1 2
4
 p

pср  pi, j
2
l
i, j  ld
,
pi 1, j  pi, j 1  pi 1, j  pi, j 1
pср 
4
Экзам вопрос:
Вычислить
геострофический вихрь по
данным на сетке с шагом
r=200 км на широте 450N.
 P0=996гПа, P1=991гПа,
P2=990гПа, P3=998гПа,
P0=1001гПа.
 Плотность воздуха у
земной поверхности
задать самостоятельно.

Экзам вопрос:

Вычислить геострофический вихрь в
точке карты, расположенной между
круговыми параллельными
циклоническими изобарами 990 и 995
гПа на широте 450N. Радиус кривизны
изобар 600 км
– Плотность воздуха у земной поверхности
задать самостоятельно.
Величина
(+f)· ρ-1
называется потенциальным вихрем
Потенциальный вихрь – это скалярная
характеристика точки.
 Он показывает, как вращение воздуха
связано с толщиной вращающегося слоя
между изоэнтропическими
поверхностями ( =const).
 Исследование потенциального вихря
объясняет многие черты циркуляции
атмосферы и широко применяется в
практике (США, Англия, Индия)

Для справки: распределение потенциальной
температуры над станцией и в разрезе
Из термодинамики
Q
dЭ 
 Э  ln( )  const ,
T
 p1000 
 T
 p 


Линии (поверхности) одинаковой потенциальной температуры
(=const) называются
изоэнтропическими
R/c
p
Потенциальный вихрь: откуда возникает
это понятие?
Применим теорему Бьеркнеса для вычисления циркуляции C
относительного движения бесконечно малого контура с площадью S
DC
а
Dt
 
dp
, где C  C  C , C  S , С  2 cos S  f S
а
e
e

В случае адиабатического движения в каждой частице атмосферы
потенциальная температура  постоянна: d /dt = 0
Т.е. на поверхности  =const в каждой частице воздуха в силу
уравнения состояния плотность выражается через давление и
потенциальную температуру:
 p0 
 T 
 p 
 
R/c
R/c
R/c
p  p0  p
p  p0  p


 
 
R  p 
R p 
R/c
dp
d
откуда следует, что 
  dp p  0   S   f   0

dt
p
Т.е на поверхностях  =const частица воздуха сохраняет угловой момент
Размерность, порядок и единицы
потенциального вихря
Обозначают - PV
 Размерность :
[PV]=[(+f)]·[ ]·[ρ-1 ]=c-1Kм-1м3кг-1
=м2·К·с-1·кг-1
 Порядок: O(PV)=O(f·д/дz· ρ-1)=
=10-4[c-1]·10[K]/1000[м]/1[кгм-3]
=10-6[м2·К·с-1·кг-1]
 На карту наносят в единицах
1 PVU=PV·105

Т.е. при адиабатическом движении бесконечно
малый контур на изоэнтропической поверхности
сохраняет свой момент импульса: S(+f)=const
Перейдем от контура к точке, для чего
выразим площадь контура через его
массу, деленную на плотность и
высоту:
 M   z ,
но  M   z S
откуда
S 
M
 z
поэтому
В адиабатической атмосфере
между двумя близкими
изоэнтропическими
поверхностями будут все время
одни и те же частицы, т.е. масса
сохранится, так же как и 
S 
 M  M 




 const
 z  z   z
значит  S (  f ) 
  f 

 const
 z
Значит:
Потенциальный вихрь –
 это угловой момент частицы,
который сохраняется при движении
по изоэнтропический поверхности



  f 
d    f  

 const или 

0


z
dt  
z
Здесь определение, физическая интерпретация
и уравнение сохранения для потенциального вихря!
Важное следствие- уточнение механизма
образования вертикальных токов в
атомсфере:
справедливы уравнения
d    f  
w
1 d


0
и

dt  
 z 
z  l    dt
1  d   f
d  1  

   f  
0

 z
dt
dt    z 

w
d
 
g
   f 
   f    g
0
p
z
dt   p 
 p   g  z !!
1
  
w
 

z

p



d   


dt   p 
Причина
вертикальных
токов в
атмосфере –
 Это изменения
градиента
потенциальной
температуры
при
перемещении
частиц воздуха

Основоположники теории
потенциального вихря
Ганс Эртель, немец
Карл-Густав Россби, швед
Применение потенциального
вихря (NWS USA)
04 July
2005/12.00 UTC Vertical cross
section;
black: isentropes
(ThetaE),
dark green thin:
potential vorticity
<1 unit,
dark green thick:
potential vorticity
>=1 unit,
orange thin: IR
pixel values,
orange thick: WV
pixel values
Поперечное сечение изоэнтропических
поверхностей (тонкие линии)


Толстая линия – тропопауза (на ней PV=2)
Изотахи (сплошные – направление внутрь,
пунктирные – наружу) циркуляции воздуха
Два фактора, изменяющих вращение атмосферных
потоков : широта и высота гор (северное полушарие)
(+f)· ρ-1=const
Если стратификация становится устойчивее
(растет расстояние между изотетами) вращение
должно усиливаться
При движении к полюсу растет
переносный вихрь и Zn вращ
должно убывать
Следствия: западный
поток не должен
поворачивать к
северу или югу, а
восточный способен
это делать, сохраняя
абсолютный вихрь
Изменение потока при сохранении
потенциального вихря. 1) восточный
поток
1)Для сохранения вихря восточный поток должен обтекать гору с
циклоническим искривлением траектории (справа).
2)Над горой собственное вращение усиливается, поэтому траектория
должна повернуть антициклонически и вернуться к исходному
направлению
Изменение потока при сохранении
потенциального вихря. 2) западный поток
1) При первоначальном подъеме поток начнет поворачивать циклонически
за счет уменьшения высоты
2)Для сохранения вихря западный поток должен начать обтекать гору с
антициклоническим искривлением траектории (слева).
3)Опускаясь он ускоряет вращение и усиливает антициклоничность
4)Для сохранения потенциального вихря траектория должна повернуть
циклонически и вернуться к исходному направлению
5) Но любое отклонение от прямолинейного западного потока нарушает
сохранение абсолютного вихря. Поэтому траектория становится
волнообразной.
В южном полушарии
этот эффект
проявляется в западном
потоке
так:
Значения вертикальной и
горизонтальных составляющих вихря
L  1000 км, H=1 км, U=V=10 м/с, W=10-2 м/с
 w v  W V
O
 

 108  102 с1 
 y z 


L
H


 u w  V W


 102  108 с1 




L
 z x  H
 v u  U V
5
5
5  1 
      10  10  10 с 
 x y  L L

В атмосфере вихревые трубки располагаются:
– Почти горизонтально
– То, что видим от ИСЗ – это расположение в
горизонтальной плоскости самих вихревых трубок
Спиральность нужна для характеристики
вращений в вертикальных плоскостях
(поперечных циркуляций)
Спиральность - это



Джордж Кейт
Бечелор,
Один из крупнейших
гидродинамиков ХХ
в, австралиец.
Мера наклона оси
вихря по отношению
к вектору скорости
течения
Она используется при
изучении вторичных
циркуляций, т.е.
отклонений течений
от основного потока
Расчет спиральности
– это обязательная
информация для
метеослужбы США
Математическое определение
S  V  rotV  V  (  V )
или
i

S  V
x
u
  w v 
 v u 
k
 u w 
  v 

u 
 w  
 z x 

  y z 
 x y 

z 
10*10-2
10*10-2
10-2 *10-5
w 
c большой точностью
u
v

v
2
S  v u   V
, где tg  
z
z
z
u
j

y
v
Знак спиральности определяется поворотом ветра с высотой!
Доказательство для любознательных
vu   uv
u 
 u 

2
1)   
 vu   uv  v   
vz
vz
v2
1 
u
 u 

2)    ctg       ctg   z  
v
vz
sin 2  z

 u 
2
2
3) v  V  sin   v     V
z
vz
u
v

v
2
S  v u   V
, где tg  
z
z
z
u
Диапазон значений



Спиральность – это скалярное произведение векторов
rotV·V=|rotV||V|cos( rotV,V)
Если вектора перпендикулярны (скорость
горизонтальна, а вихрь вертикален спиральность – нуль)
Если вектора параллельны или антипараллельны,
спиральность максимальна по модулю.
Зачем нужно вычислять
спиральность
Спиральность в первую очередь полезна
потому, что позволяет количественно
оценить вращение в поднимающемся воздухе
конвективных ячеек
 Если такое вращение обнаруживается, то
велика вероятность, что конвективная ячейка
превратится в суперячейку со всеми ее
опасными явлениями (ливни, грозы, град,
шквал, смерчь)

Преобразование горизонтального
вращения в вертикальное. 1 случай

Воздух в ПС
всегда имеет
вертикальный
сдвиг скорости.
Если он
движется, огибая
гору, то
вертикальный
сдвиг резко
усиливается
Если такой воздух поднимается вверх, например в гору, то
вращение из горизонтального становится вертикальным (по
обе стороны горы разного знака)
Преобразование горизонтального
вращения в вертикальное. 2 случай


На рисунке
видно, что сдвиг
СКОРОСТИ ветра
порождает
горизонтальное
правое вращение
Причем вихревые
трубки (роллы)
ориентированы с
юго-востока на
северо-запад
Но на нижнем уровне воздух втекает в конвективную ячейку с
востока и вращение способствует его подъему.
Но подъем изменяет вращение. Из горизонтального оно
становится вертикальным.
Мезопрогноз на 24 ч для Флориды 4.11.98
(возник ураган Mitch
Энергия неустойчивости (слева)
 Индекс спиральности (справа)
 Совпадение областей максимумов указывает на
возникновение суперячеековой конвекции

Выводы:
Для преобразования горизонтального
вращения в вертикальное необходим
сдвиг не только скорости, но и
направления ветра.
 Значение спиральности отражает оба
эти фактора в одном скалярном
критерии.
Именно поэтому этот критерий все шире
распространяется среди метеорологов

Добавка для любителей торнадо:
Воронка в ванной
Представьте себе ванну с неглубокой и
неподвижной водой.
Когда сток открывается, вода начинает
вытекать, образуя радиальный поток в
направлении стока и ускоряясь под
влиянием гравитационной силы по мере
приближения к сливному отверстию.
Таким образом, сначала устанавливается
плавный, единый вертикальный поток без
заметного вращения.
Однако это состояние потока удерживается недолго.
Мелкие нерегулярности в движении воды, движении
воздуха над поверхностью воды и возмущения в трубе
стока приведут к тому, что с одной стороны стока
окажется немного больше воды, чем с другой,
и тогда в потоке появляется заметный вихревой,
круговой компонент движения.

По достижении определенной
скорости вращения в игру
вступают центробежные силы:
они отталкивают воду от стока
по радиусу. Как результат, на
изначально плоской
поверхности воды над стоком
образуется углубление,
которое быстро превращается
в воронку.
– В конце концов внутри
водоворота формируется
миниатюрный воздушный
торнадо, а на водной
поверхности воронки
возникают достаточно
сложные нелинейные
структуры - барашки, волны и
завихрения.
Беспрерывное ускорение завершается новым
устойчивым состоянием.
Действующие силы теперь
взаимосвязаны через
самобалансирующиеся петли обратной
связи, которые обеспечивают
устойчивость структуре водоворота в
Через некоторое время
сила тяготения,
влекущая воду вниз в
направлении стока,
давление воды,
направленное внутрь
потока, и
центробежные силы,
расталкивающие поток
в стороны,
уравновешивают друг
друга;
устанавливается
устойчивое
состояние, в
котором тяготение
поддерживает
поток энергии
высокого уровня, а
трение рассеивает
некоторую
небольшую ее
Итак: по мере того как частицы воды
движутся вниз в направлении стока, их
радиальная и круговая скорости
нарастают.
Радиально они ускоряются под
действием силы гравитации,
а скорость вращения возрастает
оттого, что уменьшается радиус
вращения:
так фигуристка ускоряет обороты,
прижимая руки к телу при
выполнении пируэта.
В результате частицы воды движутся
вниз по спиральным траекториям,
образуя сужающуюся трубку линий
потока, известную как воронка.
•Так как основной поток все еще радиален и направлен к
центру, воронка непрерывно сдавливается под напором воды
со всех сторон. Это давление уменьшает ее радиус и еще
больше ускоряет вращение.
•Сила тяготения, давление воды и постоянно
уменьшающийся радиус воронки - все это, вместе взятое,
непрерывно ускоряет вихревое движение жидкости.





Подобные высокоустойчивые диссипативные структуры
(торнадо)образуются иногда во время грозы при особых
атмосферных условиях.
Торнадо могут перемещаться на огромные расстояния и
высвобождать разрушительные силы, не проявляя значительных
изменений в структуре своего вихря.
Подробности процессов в этих атмосферных вихрях гораздо
богаче, чем в случае воронки воды в ванной, поскольку здесь
появляется несколько новых факторов - разница температур,
расширение и сжатие воздуха, эффекты влажности, конденсация
и испарение и т. п.
Соответственно, гораздо более сложными и разнообразными,
чем в водоворотах, оказываются структуры воздушных вихрей и
режимы их поведения.
Грозы могут превращаться в диссипативные структуры
характерных размеров и форм; при особых условиях некоторые
из них даже разделяются на два отдельных вихря.
Все! Пошли домой мыться!