MS PowerPoint, 5,22 Мб
реклама
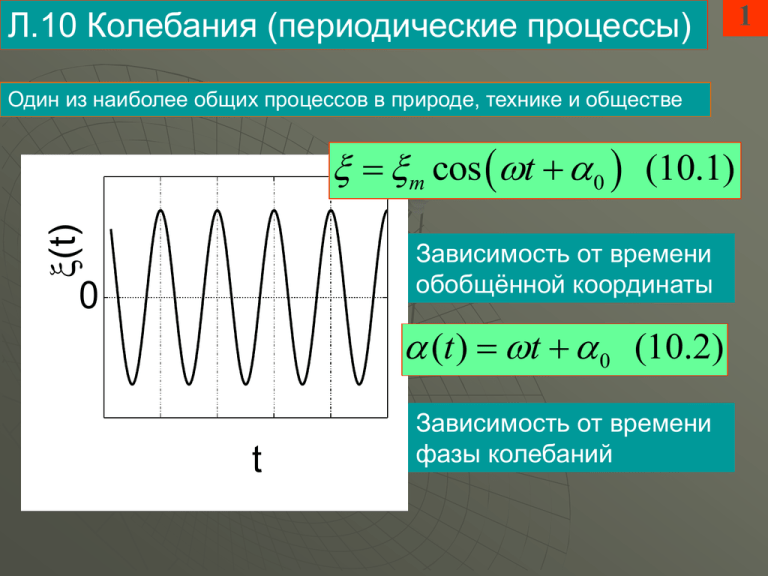
Л.10 Колебания (периодические процессы) Один из наиболее общих процессов в природе, технике и обществе (t) m cos t 0 (10.1) Зависимость от времени обобщённой координаты 0 (t ) t 0 (10.2) t Зависимость от времени фазы колебаний 1 2 Об обозначениях – они перекрылись! (10.1a) m cos t 0 (10.1) dt (10.1b) Циклическая частота колебаний и волн Угловая скорость АТТ, и это плохо Поэтому угловая скорость АТТ теперь, и внести изменения в буклет dt (10.1c) 3 Анализ одномерного движения с помощью графика ПЕ – финитное движение является периодическим Wp Потенциальная яма колебания Потенциальный барьер. Классически Запрещённая область W x1 x2 x3 x 5 тыс. лет назад – периодические колебания уровня Нила привели к возникновению древнеегипетской цивилизации Любое земледелие представляет собой периодический процесс, определяющийся сменой времён года 5 Климат Земли примерно периодически изменяется от тёплого к ледниковому и обратно 7 9 Электроэнергия передаётся от производителя к потребителю с помощью переменного (периодического) тока 11 Классификация колебаний Линейные: малая амплитуда ( m ) Свободные незатухающие 0 Затухающие Вынужденные 0 0 , 0 резонанс Нелинейные: «большая» амплитуда Слабо нелинейные ( m ) 0 , 20 , .. ( m ) Автоколебания: энергия от источника постоянной «силы» согласованно передаётся ГО Параметрические колебания: изменение амплитуды достигается периодическим воздействием на параметры ГО (t) 13 m cos t 0 (10.1) 0 v(t) t v m sin t 0 (10.3) a(t) 0 t a 0 t m cos t 0 (10.4) 2 Самые простые и важные – свободные (незатухающие) линейные (гармонические) колебания (эксперимент) 17 Основное свойство линейных колебаний: их частота не зависит от амплитуды, она определяется параметрами осциллятора Условия возникновения линейных колебаний: 1) Наличие у системы состояния устойчивого равновесия (ПЭ, консервативный элемент) 2) Наличие у системы инертности (КЭ, инерционный элемент) 3) Малые отклонения от положения УР (малые амплитуды колебаний, линейная возвращающая сила) НУР УР F k (10.5) Основные формулы для свободных (незатухающих) линейных (гармонических) колебаний m 2 k 2 W (10.6) 2 2 k 0 (10.7) m 18 Полная энергия ГО (не зависит от t ) Собственная частота ГО m cos 0t 0 (10.8) Зависимость обобщённой координаты ГО от времени при свободных колебаниях 19 Примеры гармонических осцилляторов x м k k k Н / м m m m кг x 1) Пружинный маятник m k l0 k 0 (10.9) 0 сек 1 m l l0 x 2 mx kx W 2 2 2 (10.10) W Дж Примеры гармонических осцилляторов 20 Электрический колебательный контур q Кл k C 1 C Ф m L L Гн q L I q q C 0 1 1 (10.11) 0 сек LC LI 2 q 2 W (10.12) 2 2C W Дж Затухающие колебания: ближе к реальности, чем свободные, консервативный + инерционный + диссипативный элементы (демонстрации) (t) m 2 k 2 W (t ) 2 2 21 Энергия ГО при затухающих колебаниях убывает со временем, переходя во внутреннюю энергию среды 0 m0 exp t cos d t 0 (10.13) t Пример ГО, совершающего затухающие колебания Электрический колебательный контур Конденсатор – консервативный элемент L I q R q C Катушка – инерционный элемент Резистор – диссипативный элемент R 2L 1 сек Коэффициент затухания 22 23 Вынужденные колебания: консервативный + инерционный + диссипативный + внешняя вынуждающая сила m 2 k 2 W 2 2 Энергия ГО при вынужденных колебаниях остаётся постоянной: диссипируемая энергия в точности восполняется источником mf cos t f (10.15) Зависимость обобщённой координаты ГО от времени при вынужденных колебаниях mf Вынужденные колебания: резонансная кривая – зависимость амплитуды от частоты ВВС Резонанс – резкое возрастание амплитуды ВК при приближении частоты ВВС к СЧ ГО (демонстрации) 1 2 0 1 2 24 Пример ГО, совершающего вынужденные колебания Электрический колебательный контур L Источник периодической ЭДС I q R q C Э Э (t ) Эm cos t (10.16) Э В q qmf cos t f (10.17) 25 Квантовый осциллятор: энергия квантовой частицы при финитном движении принимает дискретные значения 1.054 1034 (квантуется) Wp 0 26 Дж сек 1 Wn 0 n (10.18) 2 W4 Малые частоты (большие периоды) – W3 квантование не ощущается W2 W1 W0 Большие частоты (малые периоды) – квантование ощущается Связь этой лекции с вопросами ННЗ - буклет 3.7. Условия возникновения линейных колебаний. 3.8. Энергия гармонического осциллятора. 3.9. Собственная частота колебаний гармонического осциллятора. 27