Лекция 10 - обратное рассеяние
реклама
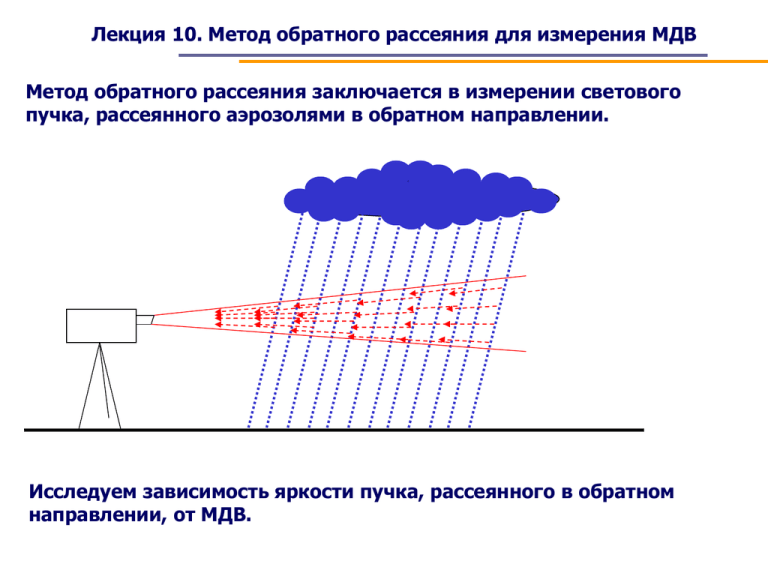
Лекция 10. Метод обратного рассеяния для измерения МДВ Метод обратного рассеяния заключается в измерении светового пучка, рассеянного аэрозолями в обратном направлении. Исследуем зависимость яркости пучка, рассеянного в обратном направлении, от МДВ. Лекция 10. Метод обратного рассеяния для измерения МДВ Пусть имеется источник света, излучающий в телесном угле α. L J0 α dL Выделим объем, заключенный внутри телесного угла α между сферическими сегментами, отстоящими друг от друга на расстояние dL . Лекция 10. Метод обратного рассеяния для измерения МДВ Площадь сегмента, ограниченного телесным углом α: sсегм 4L2 L2 4 Тогда элементарный объем толщиной dL: dV L2 dL Если число частиц в единице объема равно N, то их число в объеме dV: N dV L2 NdL Лекция 10. Метод обратного рассеяния для измерения МДВ Излучение, падающее на одну частицу, рассчитаем по закону Буге-Ламберта: J J 0 e k L J - излучение, дошедшее до частицы, J0 - яркость источника света, L - расстояние до частицы, k - показатель ослабления. Пусть все частицы одинаковые, шарообразные с радиусом r. Тогда поперечник одной частицы: S част . r 2 Лекция 10. Метод обратного рассеяния для измерения МДВ С учетом того, что все излучение распространяется внутри телесного угла α, излучение, падающее на одну частицу: Sчаст r2 Jr J 2 J 0 e k L s сегм L А излучение, рассеянное одной частицей: J рас r2 2 J 0 e k L k рас L где k рас - коэффициент рассеяния излучения частицей. Для капель k рас 0,95 . Лекция 10. Метод обратного рассеяния для измерения МДВ Будем считать рассеяние сферическим. Тогда часть рассеянного излучения, попадающее на зеркало приемника площадью s: r2 s J1 2 J 0 e 2 k L k рас L 4 L2 Или: J1 r 2 s k рас 4 L4 J 0 e 2 k L Лекция 10. Метод обратного рассеяния для измерения МДВ Излучение, полученное от всех частиц в объеме dV: J r 2 s k рас 4 L4 J 0 e 2 k L L2 NdL Интегральное излучение, полученное от всех частиц на всем протяжении луча: L J 0 r 2 s k рас 4 L2 J 0 e 2 k l NdL Или: J r 2 sk рас J 0 N 4 L 0 1 2 kL e dL 2 L Лекция 10. Метод обратного рассеяния для измерения МДВ L Обозначим: B 0 Тогда: J Nr 2 1 2 kL e dL 2 L sk рас J 0 4 B Исследуя зависимость В(L) можно заключить, что при L > 50 м интеграл В не изменятся. Тогда верхний предел в формуле для В можно принять равным 50 м. Некорректно брать нижний предел интеграл В равным нулю. С учетом того, что источник света находится внутри прибора на некотором расстоянии от стенки, примем нижний предел равным 0,5 м. Интеграл В в конечном виде не берется. Его можно взять только численно. Лекция 10. Метод обратного рассеяния для измерения МДВ J Nr 2 sk рас J 0 4 B Теперь свяжем величину обратного сигнала J с МДВ. По формуле Траберта: Sm Sm b N r2 - метеорологическая дальность видимости, b const 0,62 . Тогда: b Nr Sm 2 Подставив в формулу для J, получим: b sk рас J 0 J B Sm 4 Лекция 10. Метод обратного рассеяния для измерения МДВ L b sk рас J 0 J B Sm 4 B 0 1 2 kL e dL 2 L С другой стороны, по формуле Кошмидера, приняв ε = 0,03 , имеем: k ln 3,9 Sm Sm Значит, интеграл В также зависит от МДВ. Видно, что МДВ не может быть выражено через J в конечном виде. Обратная задача решена быть не может. Можно, однако, решить прямую задачу – выразить J через МДВ. Эту задачу можно решить только численно. Лекция 10. Метод обратного рассеяния для измерения МДВ Численное решение дает зависимость: J/J0 10-3 10-4 10-5 0 2 4 6 8 10 L км Лекция 10. Метод обратного рассеяния для измерения МДВ Выводы. 1. Зависимость J(МДВ) носит обратный характер по отношению к трансмиссометрам. 2. Для реализации метода чувствительность приемной аппаратуры должна быть гораздо выше, чем у трансмиссометров. 3. Для исключения влияния паразитных сигналов необходимо применять импульсные источники света.