Лекция10_Supercond

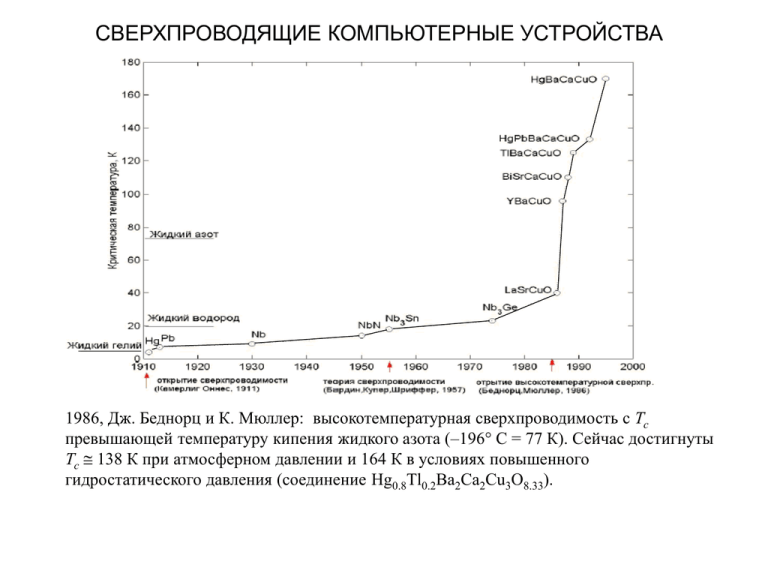
СВЕРХПРОВОДЯЩИЕ КОМПЬЮТЕРНЫЕ УСТРОЙСТВА
1986, Дж. Беднорц и К. Мюллер: высокотемпературная сверхпроводимость с Тс
превышающей температуру кипения жидкого азота (–196 С = 77 К). Сейчас достигнуты
Тс  138 К при атмосферном давлении и 164 К в условиях повышенного
гидростатического давления (соединение Hg0.8Tl0.2Ba2Ca2Cu3O8.33).
Эффект Мейснера:
выталкивание
магнитного поля
T > Tc
T < Tc
me c 2
Глубина проникновения  L 
30 – 300 нм
4ns e2
B
I рода
II рода
Hc1 Hc
Hc1
Hc2
Кривые намагничивания
сверхпроводников I и II рода
H
Зависимость критического магнитного
поля Hc от температуры
нормальный металл
Энергетическая щель
Электронная теплоемкость
E
Критический ток
Свободные состояния
2а
I
H
2ca
ca
Ic 
Hc
2
EF

Занятые состояния
  1.76kBTс ~ 410–4 эВ
Критическая плотность тока: ~1000 A/mm2
Природа сверхпроводящего состояния
Л. Купер (1956)
Пару образуют электроны с противоположными спинами и квазиимпульсами.
Пары ведут себя как бозоны. В отличие от нормальных электронов, они могут
находиться в одном наинизшем состоянии (Бозе-Эйнштейновский конденсат)
Размер пары ~ 1 мкм; среднее расстояние между частицами ~ 1 нм.
Различные пары перекрываются и образуют фактически одно целое.
При T = 0 все электроны спарены (ns = n), при T > 0 возникают нормальные
электроны: ns + nn = n.
Квантование магнитного потока
Все электроны, объединенные в куперовские пары, образуют
(r )  ns (r )ei(r )
сверхпроводящий конденсат с общей волновой функцией
1 2 22
pˆ  V
Гамильтониан H  
 V rr
4m
4m
e e
pˆ  pˆ 
2e
A r 
c
2
2
1 1  2e 2e 
H A    pˆ i A
 r 
  AV r V
4m4eme  c  c 
В равновесии плотность СП электронов постоянна, (r) ~ exp[i(r)]
Это – состояние конденсата в отсутствие магнитного поля (A(r) = 0) : H(r) = E(r).
При A(r) ≠ 0: решение HAA(r) = EA(r) в виде A(r) = (r)exp[iA(r)] ~ exp[i(r)+iA(r)].
2e 
2e 



i


A
exp
i


i






A  exp  i  i A 


A
A



c
c




2e
2e
 ei  iei
 A   A dl
Если выбрать A(r) так, что  A  A  0
c
c
 
то HAA(r) = [H(r)]exp[iA(r)] = [E(r)]exp[iA(r)] = EA(r): решение найдено!
В присутствии магнитного поля волновая функция СП электронов приобретает
дополнительную фазу A(r)
Волновая функция однозначна: при обходе по замкнутому контуру
2e
A dl  2n , n = 0, 1, 2, …

c
hc
rot
A
dS

B
dS



n

0 0 


2e
C
C
 A 
C
квант магнитного потока
0 ≈ 210–7 Гссм2 = 210–15 Вб
Нелокальное квантовое взаимодействие
Частица испытывает действие электромагнитного поля даже в тех точках, где
поле в классическом смысле отсутствует (B = 0, A  0).
Фаза волновой функции зависит от A , а не от B.
Эффект Ааронова – Бома (1949, 1959)
Когерентный пучок электронов
направляется по двум путям и
наблюдается интерференция.
Когда в соленоиде изменяется
магнитное поле, интерференционная
картина сдвигается. Между путями
возникает дополнительная разность фаз
 
e
c
 Adl 
e

  2
c
q
ch
(потому что заряд электрона вдвое меньше заряда
 2 0
e
куперовской пары).
Эффект квантовый: исчезает при h  0.
Электрический вариант: фаза зависит от скалярного потенциала  даже если E = 0.
q 
Эффект Джозефсона
~ 1 нм
Туннельный контакт (SIS)
~ 10 нм
Сэндвич (SNS)
"Мостик"
Стационарный эффект: через барьер течет бездиссипативный ток, зависящий
от разности фаз волновой функции конденсата по обе стороны
джозефсоновская фаза
Ic – критический ток джозефсоновского контакта: 10 – 104 А/см2 (<< объемного Ic)
В стационарном эффекте напряжение на контакте равно нулю.
По достижении I = Ic сверхпроводящее состояние разрушается
d
На контакте возникает напряжение, при этом фаза растет линейно: U 
2e dt
Нестационарный эффект Джозефсона:
Сверхпроводящий ток через контакт осциллирует по закону I(t) = IcsinJ t, J = (2e/ħ)U
Постоянное напряжение вызывает переменный ток!
483.6 МГц/мкВ
Электронные пары, пересекающие барьер несут энергию 2eU
ħ излучается
Идеальное преобразование напряжения в частоту.
Самые точные измерения e/ħ
Квантовый стандарт вольта: точность 10–10
Вольт-амперные характеристики джозефсоновского перехода
I  I c sin  
U
dU
C
If
Rn
dt
U
d
2e dt
I 2f 
4 k BT
f
Rn
Vc  I c Rn
Контакт с малой емкостью (SNS или
Контакт с большой емкостью
мостик), Rn – нормальное сопротивление
(туннельный): развитый гистерезис
контакта
Графики описывают постоянную составляющую напряжения.
Присутствуют еще высокочастотные модуляции (джозефсоновская генерация),
обусловленные нестационарным эффектом.
Нестационарные процессы харакdI
d

теризуются джозефсоновской
U  L  LI c cos 
L cos  
 0  LJ
dt
dt
2eI c 2I c
индуктивностью
Сверхпроводящий квантовый интерферометр
Сверхпроводящее кольцо с
джозефсоновским переходом
e = HS
30/2
H
B
A
0/2
I
I
A
I  I c sin 
t
Ic
   A  B   d 
B
2e
2e

 A  B   A dl  2  e  2 e
c B
ch
0
A
–Ic
 2
0
Связь джозефсоновской фазы с магнитным
потоком:
Макроскопическая квантовая интерференция 0
I = Ic когда  = , т.е. e = 0/2
Ток в кольце периодически зависит от
внешнего магнитного потока.
В джозефсоновском контуре  может изменяться скачком на 0 .
Запись и хранение магнитного потока n0 .
t
Изложенная картина упрощена
На самом деле набег фазы при обходе контура связан с магнитным потоком
внутри кольца: поэтому для возникновения экранирующего тока необходимо
частичное проникновение магнитного поля в контур.
Полное экранирование внешнего поля – только в полностью сверхпроводящем кольце.
1
d
При изменении потока на переходе U  d  
2e dt
dt
возникает напряжение
Это в точности соответствует приросту фазы
при обходе СП контура

 
      2
0
 2e 
2e
2e
A
dl

2



c
ch
Полный поток: суперпозиция "внешнего" е и индуцированного    e  LI
  2
LI I
e
L
 2
I  e  2 c
0 Ic
0
0
 A  B 

L LJ  l
  l sin   e
Уравнение интерферометра:
  e  l sin 
При l < 1 поток не квантуется:
Малые Ic и L не дают развиться
достаточному экранирующему току
При l >> 1 переключение:
возможные значения потока  n0
e
Двухконтактный интерферометр
В отличие от 1-контактного, среднее
U
напряжение U между двумя точками
контура может отличаться от нуля.
Ib/2
Ib
Транспортный
ток
Ib
Is
Ib/2
В отсутствие магнитного поля
критический ток Ib = Ib0 = 2Ijc
При появлении магнитного поля
в контуре наводится экранирующий ток Is
Переключение контура в нормальное состояние
происходит при
Ib/2 + Is = Ijc
Ib = Ibs = 2(Ijc – Is )
Наименьший ток переключения – когда
e = 0/2+n0, наибольший – когда e = n0
Ibr
Ib0
Рабочий ток
Ibs
U
e
При изменении магнитного потока ВАХ модулируется
между двумя крайними положениями 
Периодическая зависимость напряжения от потока
 ~ 10–6 0 Гц–1/2  310–15 ТлГц–1/2;
Сверхчувствительные датчики
по энергии Е ~ hГц–1
магнитного поля (SQUID'ы):
В живых тканях до 10–9 Тл
Цифровые устройства
Работа в сверхпроводящем режиме + низкая температура 
предельно малая диссипация на частотах < f = 2/h (для Nb f = 700 ГГц)
1 мкВт на элемент при частоте 100 ГГц
Главное ограничение быстродействия п/п элементов – перезарядка емкостей
соединений и невозможность их уплотнения из-за роста диссипации и помех
Сверхпроводящие соединения решают эти проблемы
Возможна передача пикосекундных импульсов без дисперсии и ослабления на
расстояния порядка сантиметров
Скорость передачи определяется скоростью света
Низкая диссипация и отсутствие помех позволяет "сблизить" элементы и линии
передачи  дополнительное повышение скорости
1 ГГц процессор: 50 Вт/см2;
эл. плита 10 Вт/см2
Криотрон
Катушка: Hс = 2000Гс (Nb), проволока: Hс = 100 Гс (Ta)
Поле в соленоиде H' = 4NI'/c
Ток переключения I'm = (c/4N)Hс
I'
 = 10 мкс
I
I'
100 нм
I
Токовый механизм переключения: джоулевы потери
 = 1 нс
Логика на уровнях напряжения (latching logic)
Логические 0 и 1 кодируются уровнями напряжения (как обычно)
Используются гистерезисные свойства туннельных переходов
"0" – переход в СП состоянии, U = 0
"1" – переход в резистивном состоянии, U > 0
IinIin++IbIb=–IsjU/R
(U)=+IsjU/R
(U)
Прямое переключение "0"  "1" – за счет небольшого управляющего тока Iin ,
время – пикосекунды.
Обратное переключение требует снятия тока смещения Ib и наносекундной
задержки.
Логические сигналы не в состоянии переключать, необходима внешняя
синхронизация: дополнительное время и мощность.
Передача мощных сигналов увеличивает помехи.
Созданы элементы с быстродействием несколько ГГц, но это не оправдывает
затрат на охлаждение и поддержку СП состояния
10-слойная планарная структура сверхпроводниковой интегральной схемы
Junction
Resistor
Au
Si
Mi – металл (Nb), Ii – изолятор
Планарная технология более проста, чем у полупроводниковых микросхем.
Не требуется высокотемпературная диффузия, ионная импланатация, …
Стандартные кремниевые подложки, осаждение нескольких слоев металла и
диэлектрика
Быстрая одно-квантовая логика (RSQF logic)
Информация кодируется квантами магнитного потока
Элементарная ячейка – сквид-интерферометр с двумя возможными состояниями
мВ
пс
Переключение: внешний магнитный поток (например, ток Ie подводится к участку
петли и создает поток Φe = MIe); M – индуктивность участка
Физически: поток проникает через переход и создает импульс напряжения
U t  
d
dt
 U  t  dt   0
в единицах фазы:  2   0   U  t  dt  2
площадь импульса всегда постоянна:
Амплитуда ~ мВ, площадь 2мВ·пс
Информация хранится в виде магнитного потока, передается в виде импульсов
напряжения
Поток  джозефсоновская фаза, 2-импульс  скачок фазы на 2
100 мкА
0.1 пФ
2·10–19 Дж
(в п/п 10–13 Дж)
ОСНОВНЫЕ ЭЛЕМЕНТЫ RSFQ ЛОГИКИ
Линия передачи SFQ импульсов
Каждая ступень – 2-контактный сквид, токи смещения I1, I2, ...,
обеспечивают подкритическое начальное состояние.
Ток со входа А переключает J1 в нормальное состояние, ток начинает
поступать на J2 и т.д.
Иными словами: скачок фазы в J1 возбуждает SFQ импульс в J2 ...
Задержка D = 40 на каскад
Полоса >1 ТГц, форма импульса автоматически поддерживается, шум фильтруется
Разветвитель
Переключение J0 увеличивает
эффективный поток в ветвях
L4-J1 и L5-J2
Переключение J1 и J2
порождает SFQ импульсы на
выходах Q1 и Q2
Булевы функции
Переход смещен так, что переключить
его могут только два импульса вместе:
И
Переход смещен так, что переключить
его может любой из импульсов:
ИЛИ
Триггер
Основа – интерферометр J3-L-J4.
Пусть начальное состояние |0:
циркуляция тока против часовой стрелки
SFQ импульс с входа S переключает J3 и ток
начинает течь обратно: |1.
Обратное переключение: SFQ импульс на
входе R
На J4 развивается SFQ импульс и поступает на F
Переходы J1 и J2 вспомогательные. Если на R поступает сигнал, когда схема находится
в состоянии |0, то переключается J1, и сигнал на интерферометр не проходит
Информационный протокол RSFQ систем
Рассматривались асинхронные элементы: выходной сигнал формируется сразу
после входного
Существенно импульсный характер сигналов требует особого истолкования
Ячейка содержит асинхронные компоненты и может находиться в 2 или более
устойчивых состояниях
Входы: данных (информационные) и тактовые
Тактовые – команда на формирование начального состояния ячейки и
выходного сигнала
Информационный сигнал интерпретируется как |1, если SFQ импульс поступает
в течение временного интервала, задаваемого тактовыми импульсами (D1).
Отсутствие импульса в этом интервале рассматривается как |0 (D2).
В ожидании тактового импульса входные сигналы хранятся и частично
обрабатываются
Пример реализации этого протокола: рассмотренный выше триггер
Вход S – информационный, R – тактовый.
Цикл начинается с тактового импульса,
который устанавливает |0
Если на протяжении тактового периода не
было сигнала S, то следующий тактовый
импульс переключит J1, на выход F сигнал не
проходит
Если сигнал S был, интерферометр перешел в
состояние |1.
Тактовый импульс переключает J4, и SFQ
импульс поступает на F.
CLC
Вентиль ДА: входной сигнал воспроизводится
с задержкой до появления тактового импульса
Вентиль НЕТ: инвертор
Самосинхронизация: тактовые и
информационные импульсы имеют одинаковую
физическую природу
J5
Общие характеристики RSFQ логики
1. Число джозефсоновских контактов сравнимо с числом p-n переходов в
полупроводниковых схемах, выполняющих аналогичные функции.
2. Потребляемая мощность определяется не джозефсоновскими
контактами, а диссипацией в резисторах питания (< 1 мкВт на вентиль)
3. Допуски на значения параметров лежат между ±20 и ±30%, что
приемлемо для современного уровня низкотемпературной техники.
4. Самое главное – высокая скорость. При 3.5-мкм технологии достижима
тактовая частота 100 ГГц. Субмикронная технология позволяет ожидать
500 ГГц
5. Обычная планарная технология изготовления, более простая, чем у
полупроводниковых схем
6. Созданы полные наборы элементов RSFQ логики, объединенные в
чипы с интеграцией ~ 104 джозефсоновских переходов. Нет технических
препятствий для создания полноценных микропроцессоров.
7. Перспективы использования высокотемпературной сверхпроводимости
8. Объект квантовый, вычисления классические
Одноэлектронный транзистор
Заряд конденсатора через резистор: заряд
растет плавно, пропорционально
приложенному напряжению
Вместо
резистора –
туннельный
переход.
Заряд на островке растет ступенчато
("кулоновская лестница"). Ступеньки
"скругляются" с ростом температуры и
проницаемости перехода.
Cg
Q 2 Cg
Wa 

QU
2C C
1
Wa 
 ne  Qe 2  const
2C
Qe = CgU
Пока (n – 1/2)e < Qe < (n + 1/2)e
энергетически выгодно, чтобы на
островке был заряд ne
Условия: время туннелирования t <<
других характерных времен, в т.ч.
интервала между отдельными актами
туннелирования; t ~ 10–15 c.
Малая прозрачность барьера исключает
одновременное туннелирование двух и
более электронов:
R >> RQ = h/4e2 ~ 6.5 кОм.
Работа "добавления" электрона e2/2C > kT .
Характерная емкость C = e2/kT ~ 10–15 Ф при 1 К
Возможно надежное изменение заряда на 1 е в системах с огромным числом электронов.
Al островок ~ 100 нм содержит около миллиона электронов.
– V/2
исток
затвор
I(t)
U
Порог:
кулоновская
блокада
сток
+ V/2
t
Периодическая
зависимость порогового
напряжения от
= UC потенциала затвора
Wa 
1
 ne  Qe 2  const
2C
•
•
•
•
Применения
Сверхчувствительная электрометрия. Вблизи порога
кулоновской блокады малейшие изменения внешнего
заряда приводят к заметным вариациям тока: 10–5e/Гц
при частоте 1 MHz.
Сканирующая микроскопия. Одноэлектронный
транзистор на острие зонда: комбинация
субмикронного пространственного разрешения и
субэлектронного разрешения по заряду.
Бистабильные одноэлектронные устройства:
одноэлектронная логика.
Одноэлектронная спектроскопия: измерение уровней
энергии в квантовых точках и других нанообъектах.