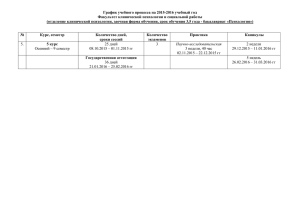
Третий закон Ньютона

КЛАССИЧЕСКАЯ
ДИНАМИКА.
ЗАКОНЫ НЬЮТОНА
07.05.2016
1
Динамика (от греческого dynamis  сила) –
раздел механики, посвященный изучению
движения материальных тел под действием
приложенных к ним сил. В основе классической
динамики лежат законы Ньютона, из которых
получаются все уравнения
и теоремы,
необходимые для решения задач динамики. Как
и другие принципы, лежащие в основе физики,
они являются обобщением опытных фактов.
07.05.2016
2
3.1. Инерциальные системы
отсчета. Первый закон
Ньютона
В различных системах отсчета законы движения
имеют, в общем случае, различный вид. Однако всегда
можно найти такую систему отсчета, в которой законы
механики имеют наиболее простой вид. Это система
отсчета с однородным и изотропным пространством
и однородным временем. Такая система отсчета
называется инерциальной.
07.05.2016
3
В инерциальной системе отсчета всякое
свободное движение происходит с постоянной
по величине и направлению скоростью.
– это утверждение составляет содержание
первого закона Ньютона  закона инерции.
Стремление тела сохранить состояние покоя или
равномерного прямолинейного движения называется
инертностью.
07.05.2016
4
Во всех инерциальных системах свойства
пространства и времени одинаковы и одинаковы
все законы механики. Это утверждение
составляет
содержание
принципа
относительности Галилея.
Координаты одной и той же
точки в разных системах
отсчета K1 и K2, из
которых K1 движется
относительно
 K2 со
скоростью  , связаны
друг с другом соотношением
07.05.2016
  
r2  r1   t
5
  
r2  r1   t
07.05.2016
6
Принцип относительности Галилея
можно
сформулировать
инвариантности
как
уравнений
требование
механики
по
отношению к преобразованиям Галилея:
t1 = t2 = t,
  
r2  r1   t
07.05.2016
7
Из первого закона следует важный
физический
принцип:
существование
инерциальной системы отсчета. Смысл первого
закона состоит в том, что если на тело не
действуют внешние силы, то существует
система отсчета, в которой оно покоится.
Следствием первого закона Ньютона является
утверждение, что если наблюдатель находится в
инерциальной
системе
отсчета,
а
это
удостоверяет покоящееся в ней тело, то все прочие
тела, на которые не действуют силы, будут
также находиться в покое или двигаться с
постоянной скоростью.
07.05.2016
8
Второй закон Ньютона.
Второй закон Ньютона количественно
определяет, как изменяется состояние движения
тела под действием внешних сил.
Под силой в механике понимают всякую
причину, изменяющую состояние движения
тела.
07.05.2016
9
Всякое тело оказывает сопротивление при
попытках привести его в движение или изменить
модуль или направление его скорости. Это свойство
тел называется инертностью.
Мера инертности тела называется массой.
Импульсом или количеством движения
системы материальных точек назовем
векторную сумму импульсов отдельных
материальных точек, из которых эта система
состоит.
07.05.2016
10
Для системы из двух материальных
точек


 

р  р1  р2  m11  m2 2
В инерциальной
системе
отсчета

изменение импульса р материальной точки со
временем представляется уравнением:


dр d m  

F
dt
dt
07.05.2016
11
Для медленных движений, когда импульс
пропорционален скорости:


F  m d
dt

 ma
Величина F, равная скорости изменения
импульса во времени, называется силой,
действующей
на
рассматриваемую
материальную точку.
07.05.2016
12
Таким образом, в инерциальной системе
отсчета
производная
импульса
материальной точки по времени равна
действующей на нее силе.
Это утверждение называется вторым
законом Ньютона, а соответствующие ему
уравнения
–
уравнениями
движения
материальной точки
07.05.2016
13
Третий закон Ньютона
Третий
закон
динамики
Ньютон
сформулировал так: “Действию всегда есть
равное и противоположное противодействие;
иначе  взаимодействия двух тел друг на друга
между собой равны и направлены в
противоположные стороны”.


F12   F21
Третий закон отражает тот факт, что сила
есть
результат
взаимодействия
двух
различных тел.
07.05.2016
14
Третий закон ничего не говорит о величине
сил, а только о том, что они равны. Здесь очень
важно отметить, что в третьем законе идет речь о
силах, приложенных к различным телам.
Он выполняется в случае контактных
взаимодействий, т.е. при соприкосновении тел,
а также при взаимодействии тел, находящихся
на расстоянии друг от друга, но покоящихся
друг относительно друга.
07.05.2016
15
Закон изменения импульса
Третий закон Ньютона в соединении с его первым и
вторым законами позволил перейти от динамики
отдельной
материальной
точки
к
динамике
произвольной механической системы.
Принято силы, с которыми взаимодействуют
между собой составные части системы, называть
внутренними силами.
Внешними называются силы, с которыми вся
система или отдельные тела, входящие в ее состав,
взаимодействуют с окружающими телами.
07.05.2016
16

F
Обозначим
– результирующая всех внешних
сил приложенных к i-ой точке системы.
По второму закону Ньютона можно записать
систему уравнений:
внеш.
i
 внеш. 



d
m1υ1   F1  F12  F13  ...  F1n ,
dt
 внеш. 



d
m1υ2   F2  F21  F23  ...  F2n ,
dt
......... ...............................,
 внеш. 


d
m1υn   Fn  Fn1  ...  Fn,n1.
dt
07.05.2016
17
Сложим
и сгруппируем попарно
 эти уравнения

силы F и F :
n
n 





d
внеш.
 dt mi υi    Fi  F12  F21  ...  Fn1,n  Fn,n1 .
i 1
i 1


По третьему закону Ньютона
Fik  Fki  0 , тогда

n
n 

d
dp
внеш.
 dt mi υi    Fi  dt .
i 1
i 1
ik
ki




 n  внеш.
Назовем F   Fi
– главным вектором всех внешних
i 1
сил, тогда:
07.05.2016
 
dp
 F.
dt
18
 
dp
F
dt
Скорость
изменения
импульса
системы равна главному вектору всех
внешних сил, действующих на эту
систему.
Это уравнение называют основным уравнением
динамики поступательного движения системы тел.
Так как импульс системы


p  m
то
 
d
m   F
dt
07.05.2016
19
Закон сохранения импульса
Если геометрическая сумма всех внешних

сил равна нулю, то
dp
dt
0
следовательно, р = const. То есть, если
геометрическая сумма всех внешних сил,
действующих на систему, равна нулю, то
импульс системы сохраняется со временем.
07.05.2016
20
Закон сохранения импульса
Система тел называется замкнутой
(или изолированной), если можно пренебречь
действием внешних сил по сравнению с
внутренними.
07.05.2016
21
Закон сохранения импульса
Суммарный импульс замкнутой системы
тел сохраняется при любых процессах,
происходящих в этой системе.



m1  υ1  m1  υ1
F12 
,
t   t 



m2  υ2  m2  υ2
F21 
.
t   t 




m2  υ2  m2  υ2
m1  υ1  m1  υ1

.
t   t 
t   t 
07.05.2016
22




m2  υ2  m1  υ1  m2  υ2  m1  υ1

Отсюда

m22  m11  const
Для системы из N тел:


mN N  ....  m11  const
07.05.2016
23
Сумма в левой части – суммарный импульс
системы:
n
 
 mi  υi  P  const
i 1
Следовательно,

dP
0
dt
- закон сохранения импульса в дифференциальной
форме
07.05.2016
24
Векторная сумма количества движения
или полный импульс замкнутой системы
остается постоянным при любых
взаимодействиях между телами этой
системы.
Этот закон является фундаментальным и
выполняется при любых движениях, в том числе и
релятивистских.
Из закона сохранения импульса вытекает два
важных следствия закон движения центра инерции и
закон аддитивности массы.
07.05.2016
25
Центр инерции и закон его
движения
Точку C, которая делит
расстояние между
частицами на отрезки,
обратно
пропорциональные
массам этих частиц,
назовем центром
инерции (или центром
масс) данной системы
частиц.
07.05.2016
26
L1  m1  L2  m2
Поскольку L1=XсX1, L2=X2Xс, где Xс- координата
центра инерции, то
m1  xc  x1   m2 x2  xc 
откуда
07.05.2016
m1  x1  m2  x2
XС 
m1  m2
27
Для системы из N материальных точек,
расположенных произвольным образом:
m1  x1  m2  x2  ...  mn  xn
XС 
m1  m2  ...  mn
Аналогичные выражения получаются для
ординаты Yс и аппликаты Zс центра инерции системы
материальных точек.
07.05.2016
28
Определим радиус-вектор центра инерции:
  n
 n
R    mi  ri  /  mi
 i 1
 i 1
Центром инерции (центром
системы
  масс)

частиц с радиус-векторами r1, r2 ,... rn называют
точку с радиус-вектором
n
  n

R    mi  ri  /  mi
 i 1
 i 1
07.05.2016
29
Тогда движение центра инерции для системы
частиц (в том числе для тела любой формы конечных
размеров) можно описать следующим образом
n
n



υС  dR / dt  d ( mi  ri /  mi ) / dt 
i 1
i 1

  mi (dri / dt ) /  mi 

  mi  υi / 
07.05.2016


P
mi   Pi /  mi 
М
30
Если сумма внешних сил не равна нулю, то
движение центра инерции можно рассматривать как
движение материи, в которой сосредоточена вся масса
системы и координаты совпадают с центром масс:


2


d R
dP
 M  2    Fвнешн  F
dt
 dt 
Аддитивностью вообще, называют свойство,
состоящее в том, что величина, характеризующая
систему в целом,
складывается алгебраически из
величин того же рода, характеризующих каждую часть
системы.
07.05.2016
31
Характер движения центра инерции определим для
случая m=const.
Записав выражение для Xc для двух моментов
времени и вычитая одно из другого, получим:
m1  x1  m2  x2 ...  mn  xn
X С 
m1  m2 ...  mn
С учетом

( x)
С
07.05.2016

ΔX С
 С( x )
Δt
m1 
( x)
1
 m2   ...  mn 
m1  m2  ...  mn
( x)
2
( x)
n
32





m1  υ1  m2  υ 2  ...  mn  υ n
P
υС 

m1  m2  ...  mn
M
Центром инерции системы называется
точка, скорость которой равна отношению
суммарного импульса системы к ее суммарной
массе.
07.05.2016
33
Если система частиц замкнута, то ее суммарный
импульс является постоянной величиной.
Отсюда, центр инерции замкнутой
системы совершает инерциальное движение,
т.е. движется прямолинейно и равномерно
независимо от того, как движутся отдельные
тела, из которых составлена система.
Под действием внутренних сил
движения центра инерции не меняется.
07.05.2016
скорость
34
Движение тел с переменной
массой
Импульс системы:


P  MС
Полный импульс системы частиц
равен
произведению
полной
массы

системы М на скорость её центра масс  С .
07.05.2016
35
При условии, что M =const, получим:


 внеш.

dC
dP
M
 Ma C  F
,
dt
dt

F
внешн.
где
– внешняя результирующая сила,
приложенная к системе. Необходимо очень
тщательно определять систему и учитывать все
изменения ее импульса.
07.05.2016
36
Рассмотрим движение тел с переменной
массой на примере движения ракеты, которая
движется вперед за счет выбрасывания назад
сгоревших газов.
Ракета ускоряется силой, действующей на
нее со стороны газов. Масса М ракеты все
время уменьшается, т.е.
dM / dt  0
07.05.2016
37
Реактивное движение основано на принципе отдачи.
В ракете при сгорании топлива газы, нагретые до
высокой температуры, выбрасываются из сопла с
большой скоростью  Г .
Пусть M(t), υ(t), Mυ(t) – масса, скорость и импульс
ракеты в момент времени t.
Спустя время dt масса ракеты уменьшится на dM,
скорость увеличится на dυ, а изменение импульс системы
станет равным
M  dM   d  Г dmГ  M  Fdt,
где υГ dmГ – импульс газов, образовавшихся за время dt.
07.05.2016
38
Воспользуемся законом сохранения массы:
dmГ  dM
и введем так называемую скорость газовой струи
(скорость истечения газов относительно ракеты) :
отн   Г   
Получим:
d
dM
M
  отн
F
dt
dt
07.05.2016
39
Величина   отн
dM
dt
, добавляемая к силе F
– реактивная сила, т.е. сила, с которой действуют на
ракету вытекающие из нее газы.
Уравнение
d
dM
M
  отн
F
dt
dt
впервые получено русским механиком Мещерским И.В. и
носит название уравнение Мещерского.
07.05.2016
40
При отсутствии внешних сил, действующих на
ракету, уравнение приобретает вид:
d
dM
M
  отн
dt
dt
Решение этого уравнения дает конечную скорость
ракеты:
 M0 
   отн ln 
,
M 
07.05.2016
41
М0 и М – начальная и конечная массы ракеты.
Соотношение
 M0 
 р   г ln 

 M 
называют формулой Циолковского.
Из нее следует, что для достижения скорости υ, в 4
раза превышающей по модулю относительную скорость
выбрасываемых газов, стартовая масса одноступенчатой
ракеты должна, примерно в 50 раз, превышать ее
конечную массу.
07.05.2016
42