Лекция № 10

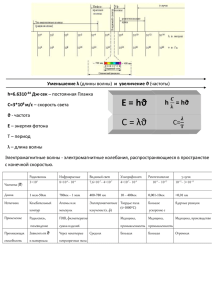
Сегодня: пятница, 6 мая 2016 г.
Ларионов В.В.
Ток смещения
К понятию «Ток смещения»
Рассмотрим ток проводимости в системе, в которую
включен конденсатор
I
L
Замкнем ключ К. Конденсатор начнет
заряжаться, следовательно по цепи
потечет ток проводимости Iпр.
Проведем произвольный контур L в
произвольной части электрической
цепи, где течет ток проводимости,
например, как показано на рисунке и
найдем циркуляцию вектора В вдоль
этого контура.

Bdl   0 I пр
Результат очевиден.

L
Однако, необходимо учесть
следующее обстоятельство.
Ток должен пересекать любую
поверхность опирающуюся на
данный контур.
Красным цветом показана поверхность, через которую
течет ток проводимости. Однако, через «синюю»
поверхность ток не течет. Поверхность проходит между
пластинами конденсатора. Возникает противоречие,
которое удается преодолеть Максвеллу. Он выдвигает
гипотезу о том, что через данную поверхность течет ток
смещения Iсм.
Следовательно, теорема о циркуляции вектора В будет
выглядеть так:

B
d
l


I


I
0
пр
0
см

L
Остается найти физический смысл тока смещения.
Рассуждения Максвелла весьма запутаны и проведены им
на уровне «веревочек и болтиков».
Мы поступим иначе. Найдем заряд на обкладках
конденсатора.
Q    S,
В формуле S – площадь пластин конденсатора, σ-плотность
зарядов на обкладках (пластинах)
К понятию «ток смещения»
т
-
-
Е
+
+
+
+
+
+
+
Воображаемую поверхность пересекают силовые линии
вектора Е(t). Изменение во времени этих векторов
и есть ток, названный током смещения
Iсм =dQ/dt= d/dt(σS)=εε0 (dE/dt)S = [dD/dt]S.
Т.к. E= σ/ εε0
Теперь теорема о циркуляции вектора В
выглядит так (во втором уравнении учтено
влияние среды):

dE
L Bdl   0 I пр   0 0 dt S

dE
L Bdl   0 J пр   0  0 dt S
Это
фундаментальное
уравнение.
Отражает сущность
электромагнетизма
Английский физик Дж. Максвелл обобщил
эмпирические закономерности, установленные
Ампером, Кулоном, Эрстедом, Фарадеем в 60-х гг.
XIX в., и сформулировал фундаментальные
уравнения
классической
макроскопической
электродинамики.
Эти уравнения описывают электромагнитные
явления в любой среде и в вакууме.
Уравнения Максвелла для электромагнитных
явлений аналогичны по своей значимости законам
Ньютона в классической динамике.
Уравнения Максвелла связывают величины,
характеризующие электромагнитное поле, с его
источниками – распределенными в пространстве
электрическими зарядами и токами.
Полная
система
уравнений
интегральной форме имеет вид
Максвелла
 D
H, d l    j d S
t 
S 

(1)
B
E, d l   
dS
S  t

(2)




в
 D, d S    dV
S
(3)
V


B,
d
S

0

S 
(4)
Полный ток, возбуждающий магнитное поле,
равен сумме токов проводимости и смещения.
Первое уравнение Максвелла в интегральной форме
говорит, что циркуляция вектора H по
произвольному замкнутому контуру Г равна
полному току, проходящему через произвольную
поверхность S, ограниченную контуром Г.
Второе
уравнение
Максвелла
служит
математической
формулировкой
закона
электромагнитной
индукции
Фарадея:
циркуляция
вектора
напряженности
электрического поля E по произвольному
замкнутому контуру Г равна скорости изменения
потока вектора магнитной индукции B через
произвольную поверхность S,
ограниченную
контуром Г
Третье уравнение Максвелла, обычно называемое
теоремой Гаусса и служит обобщением закона Кулона,
описывающего взаимодействие неподвижных зарядов:
поток вектора электрической индукции D через
произвольную поверхность S равен электрическому
заряду, находящемуся в объеме V, ограниченном
поверхностью S.
Четвертое уравнение Максвелла говорит о том
экспериментальном
факте,
что
свободные
магнитные заряды отсутствуют – поток вектора
магнитной индукции B через произвольную
замкнутую поверхность S равен нулю.
Тема:
Волны
(механические и
электромагнитные)
Электромагнитные волны – это переменные
электрическое и магнитное поле,
распространяющиеся в пространстве.
Их существование вытекает из свойств уравнений
Максвелла
Переменное во времени электрическое поле
является источником магнитного поля, которое в
свою очередь создает переменное электрическое
поле и наоборот.
Плоские электромагнитные волны
(ЭМВ) и их свойства.
Электромагнитными волнами называются возмущения
электромагнитного поля, (то есть переменное
электромагнитное поле), распространяющиеся в
пространстве.
Ограничимся простым случаем: пусть E и H зависят от
одной координаты (х) и от времени (t) (одномерная
задача).
 Ey
2
t
2

1
 Ey
2
 0 0 x
2
 Hz
1  Hz

2
2
t
 00 x
2
2
Рис.
На рис. показаны значения векторов E иH поля плоской
линейно поляризованной монохроматической волны в
различных точках луча (оси ОХ), взятые в один и тот
же момент времени.
представляет собой волновое уравнение. Всякая
функция, удовлетворяющая такому уравнению,
описывает
некоторую
волну,
причем
корень
квадратный из величины, обратной коэффициенту при
2 f
2 , дает фазовую скорость этой волны.
t
Таким образом, записанное уравнение указывает на то,
что электромагнитные поля могут существовать в
виде электромагнитной волны, фазовая скорость
которых

1
1
 0 0

(*)
В вакууме
1
    1, 
 0 0
 c  3 10 м с
8
(24)
Электромагнитные волны – поперечные волны:
векторы E и H поля электромагнитной волны
взаимно перпендикулярны так, что  E и H образуют
правую тройку векторов.
E



Н
Е
Рис.2
Взаимно
перпендикулярные
векторы E и H колеблются в
одной фазе – они одновременно
обращаются
в
нуль
и
одновременно
достигают
максимальных значений.
Модули их связаны соотношением:
 0 E  0 H ,
которое
справедливо
для
любой
бегущей
электромагнитной волны независимо от формы ее
волновых поверхностей.
Монохроматической
волной
называется
электромагнитная волна одной определенной частоты
, то есть синусоидальная электромагнитная волна,
описываемая уравнением типа Е = А Sin (t – kx). Эта
функция является простейшим уравнением (21).В
каждой
точке
электромагнитного
поля
монохроматической волны проекции векторов E и H
на оси координат инерциальной системы отсчета
совершают гармонические колебания одинаковой
Вектор Е называют световым вектором. Это
связано с тем, что на хрусталик глаза
воздействует электрическое поле. Электрическое
поле световой волны в 277 раз превышает по
мощности магнитное поле.
На фотоэлементы, фотопластинки также
основное
воздействие
оказывает
электрическое поле.
Интерференция света
Это явление широко распространено в природе,
технике, науке и является подтверждением
волновой теории света.
Интерференция
–
явление,
связанное
с
наложением двух волн и проявляющееся в том,
что в одних точках пространства, при этом,
наблюдается ослабление колебаний, а в других
их ослабление.
Необходимым условием интерференции волн
является их когерентность, т. е. согласованное
протекание во времени и пространстве двух (или
более) волновых процессов. Этому условию
удовлетворяют монохроматические волны - волны
одной строго определенной частоты и постоянной
амплитуды.
Ни один реальный источник не дает строго
монохроматического света, волны, излучаемые
любыми независимыми источниками света, всегда
некогерентны. Поэтому на опыте не наблюдается
интерференция света от независимых источников,
например от двух электрических лампочек.
Интерференция световых волн
Волновые свойства света наиболее отчетливо обнаруживают
себя в интерференции и дифракции. Для описания световой волны
воспользуемся уравнением Е1  A cos(t   )
, где Е
напряженность электрического поля волны. Две когерентные
монохроматические волны одинаковой частоты, накладываясь
друг на друга, возбуждают в некоторой точке пространства
колебания
одинакового
направления.
Напряженность
электрического поля подчиняются принципу суперпозиции,
поэтому амплитуда результирующего колебания
A 
2
2
A1

2
A2
 2 A1 A2сos( φ 2  φ1 )
Если разность фаз колебаний возбужденных волнами в некоторой
точке пространства остается постоянной во времени, то такие
волны называются когерентными. Так как волны когерентны, то
имеет постоянное
вовремени
свое в каждой точке пространства)
сos(
const
2  1 ) (но
значение, поэтому интенсивность результирующей волны (I ~A2)
I  I  I  2 I I cos( 2  1 )
1
2
1 2
В точках пространства,
где
(в максимуме
I  4I1
),
cos( φ 2  φ1 )  0
I . I1  I 2
где
, интенсивность
I  I1  I 2 когерентных
cos( φ 2 при
φ1 )наложении
0
Следовательно,
двух (или нескольких)
световых волн происходит пространственное распределение
светового потока, в результате чего в одних местах возникают
максимумы, а в других – минимумы интенсивности. Это явление
называется интерференцией света.
В случае некогерентных волн разность фаз непрерывно изменяется,
поэтому среднее во времени значение
равно нулю и
интенсивность результирующей волны всюду одинакова и при I1 =
I2 = 2I1(для когерентных волн при данном условии в максимумах I
cos( 2  1 )
= 4I1, в минимумах I = 0).
Для получения когерентных световых волн применяют
метод разделения волны, излучаемой одним источником,
на две части, которые после прохождения разных
оптических путей накладываются друг на друга и
наблюдается интерференционная картина.