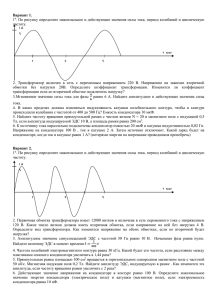
Среднее значение периодической функции a(t)

Средние, действующее значения. Слайд 1
Средние, действующее значения
1. Среднее значение периодической функции за период Т.
2. Средневыпрямленное значение периодической функции
за период Т.
3. Действующее (среднеквадратическое) значение
периодической функции за период Т.
Средние, действующее значения. Слайд 2
Среднее значение периодической функции a(t)
AСР 
1
T
t 0 T
 a(t )dt
t0
Значение АСР не зависит от выбора t0.
T
AСР
1
  a(t )dt
T0
T
T
U СР
1
  u (t )dt
T0
I СР
1
  i(t )dt
T0
Среднее значение гармонической функции за период равно нулю.
T
I СР
1
  I m sin( t   i )dt  0
T0
Средние, действующее значения. Слайд 3
Средневыпрямленное значение периодической функции
Средневыпрямленным значением периодической функции называют среднее
значение её модуля за период.
T
T
U СР В
1
  u (t ) dt
T0
I СР В
1
  i(t ) dt
T0
Для гармонической функции
T
2
U СР В
I СР В 
2

1
2
  U m sin tdt  U m  0,637U m
T 0

I m  0,637 I m
EСР В 
2

E m  0,637 E m
Средние, действующее значения. Слайд 4
Действующее значение периодической функции
Действующим значением периодической функции называется среднеквадратическое
значение этой функции за период.
T
1
2


A
a
(
t
)
dt

T0
Действующее значение периодического тока i(t) численно равно значению постоянного
тока I, при протекании которого за время T выделяется такое же количество энергии, как
и при протекании тока i(t).
T
W   Ri(t ) dt  RI 2T
2
0
T
1
2


I
i
(
t
)
dt

T0
Это для любых форм периодических токов.
Средние, действующее значения. Слайд 5
i  I m sin( t  i )
Действующее значение гармонического тока
T
T
2


i
(
t
)
dt

I
sin

 (t  i )dt 
2
2
m
0
0
I m2 T
I m2 T

dt   cos( 2t  2 i )dt

2 0
2 0
Правый интеграл равен нулю.
T
T
Im
1
1 I m2
2


I
i
(
t
)
dt

dt

 0,707 I m


T0
T 2 0
2
U
Um
2
 0,707U m
E
Em
2
 0,707 Em
Действующее значение гармонической функции в
амплитудного значения.
2
меньше её
Средние, действующее значения. Слайд 6
У других функций своё соотношение действующего и амплитудного значений.
Пример
Um2
u=Um
tИ
T
Площадь под квадратом напряжения:
U m2 t И
Поделим полученную площадь на период Т
Найдём действующее значение
U m2 t И
Т
U m2 t И
t
 Um И
Т
Т
Т
- скважность импульса
tИ