В теме «Степень числа» я знакомлю детей еще с одним... модуля. Модуль степени какого-либо числа равен степени модуля этого числа:
реклама
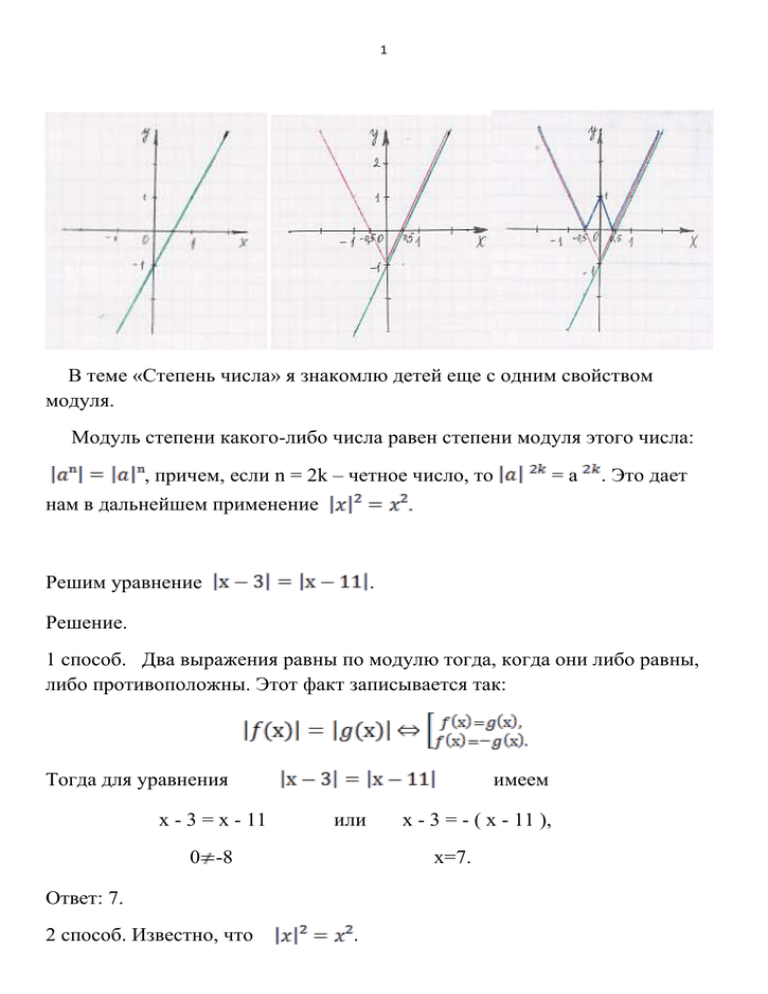
1 В теме «Степень числа» я знакомлю детей еще с одним свойством модуля. Модуль степени какого-либо числа равен степени модуля этого числа: , причем, если n = 2k – четное число, то =a . Это дает нам в дальнейшем применение Решим уравнение . Решение. 1 способ. Два выражения равны по модулю тогда, когда они либо равны, либо противоположны. Этот факт записывается так: Тогда для уравнения х - 3 = х - 11 имеем или х=7. 0 -8 Ответ: 7. 2 способ. Известно, что х - 3 = - ( х - 11 ), . 2 Используя данное свойство, можно возвести обе части данного уравнения в квадрат и получить равносильное уравнение. а) ( х - 3 ) ² = ( х - 11 ) ², х² - 6х +9 = х² - 22х + 121, 16х = 112, х = 7. б) ( х - 3 ) ² = ( х - 11 ) ², ( х - 3 ) ² - ( х - 11 ) ² = 0, ( х - 3 - х + 11 ) ( х - 3 + х - 11 ) = 0, 8 ( 2х - 14 ) = 0, х = 7. Ответ: 7. Как видите, параллельно с работой над модулем, я закрепляю умение применять формулы сокращенного умножения. Итак, по окончании 7 класса мои дети умеют использовать некоторые свойства модуля при решении линейных уравнений с одной переменной, а также строить графики линейных функций, содержащих знак абсолютной величины. 8 класс дает больше возможности для дальнейшего изучения и закрепления понятия и свойств модуля. В теме «Область определения функции» я даю задания: при каких значениях переменных не имеет смысла выражение ; . Укажите допустимые значения выражения , . 3 В теме «Сокращение дробей» при y ; при y при х . Тема «Квадратный корень из степени» учит извлекать квадратный корень из степеней, используя понятие модуль. = . «Функция y = и ее график.» Построить график функции y = . D (y): x В результате усвоения предыдущей схемы построения графиков функций, содержащих модуль, имеем случай у = f , т.е. достаточно построить график функции y = при х и отобразить ее симметрично относительно оси ординат. при k при k И, конечно, программа 8 класса позволяет нам приступить к решению квадратных уравнений, содержащих модули. При изучении неполных квадратных уравнений я даю уравнения вида 4 2х² + - 3х=0. Решение. Пользуясь правилами раскрытия модуля, имеем: 1) если х , то уравнение имеет вид 2х²+ 3х=0. 2х²-2х=0, 2х(х-1)=0, . Оба найденных значения удовлетворяют условию х , следовательно, являются корнями исходного уравнения. 2)если x , то 2х² - 3х = 0. 2х² - 4х = 0, 2х ( х - 2 ) = 0 . Оба найденных значения не удовлетворяют условию x , следовательно, в этом случае решений нет. Ответ: 0; 1. Решить уравнение x² + Используем свойство - 6 = 0. и перепишем уравнение в виде . Пусть тогда уравнение примет вид t, t t² 5 Если то = 2, х= Ответ: -2; 2. Решить уравнение . Поскольку уравнение уравнений 1) равносильно совокупности двух меем = 2) = D Ответ: 1; 8. В теме «Неравенства» я предлагаю детям неравенства вида . Пример: Ответ: Ответ: 6 В 9 классе дети научились строить графики квадратичных функций. Они четко знают алгоритм построения, определяют направление ветвей параболы, находят координаты вершины параболы, координаты точек пересечения графика функции с осями координат. Мы изучили влияние модуля на поведение графика линейной функции, поэтому можем переходить к построению графиков квадратичных функций, содержащих знак абсолютной величины. Построим графики функций а) б) в) y = г) y= а) Построим график функции . Найдем координаты вершины параболы Точки пересечения с осью Ох Парабола пересекает ось Оу в точке с координатами б) . . 7 Мы знаем, что ,если в уравнении, которым задана функция, аргумент взят по модулю, то достаточно построить график функции с теми же коэффициентами, но без модуля при , а затем отобразить его симметрично оси ординат. в) y = Если в уравнении, которым задана функция, вся функция взята под по модулю, то достаточно построить график функции, не содержащей модуль, а затем часть графика, расположенную ниже оси абсцисс, отобразить симметрично оси Ох. г) y= . Данная функция – это функция , взятая по модулю. Следовательно, ее график можно получить следующим образом: построить график функции , а затем часть графика, расположенную 8 в отрицательной полуплоскости, симметрично отобразить относительно оси абсцисс. К началу 10 класса ученики владеют понятием абсолютной величины, умеют решать линейные и квадратные уравнения, содержащие модуль, умеют строить графики функций с модулем. Это облегчит им в дальнейшем изучение более сложных уравнений и неравенств, содержащие модули. I) Уравнения вида f ( x) A, A R решаются следующим образом. Если A 0 , то корней нет. Если A 0 , то уравнению f ( x) A соответствует уравнение f ( x) 0 Если A 0 , то уравнению f ( x) A соответствует равносильная f ( x) A совокупность f ( x ) A II) Уравнения вида Способ №1 f ( x) g ( x) решаются следующим образом. 9 Уравнению f ( x) g ( x) соответствует равносильная совокупность систем g ( x) 0 f ( x) g ( x) g ( x) 0 f ( x) g ( x) Способ №2 Уравнению f ( x) g ( x) соответствует равносильная совокупность систем f ( x) 0 f ( x) g ( x) f ( x) 0 f ( x) g ( x) III) Уравнения вида f ( x) g ( x) решаются следующим образом. Способ №1 Уравнению f ( x) g ( x) соответствует равносильное уравнение f 2 ( x) g 2 ( x) Способ №2 Уравнению f ( x) g ( x) соответствует равносильная совокупность f ( x) g ( x) f ( x) g ( x) 10 IV) Уравнения вида f ( x) f ( x) и f ( x) f ( x) решаются следующим образом. Уравнению f ( x) f ( x) соответствует равносильное неравенство f ( x) 0 Уравнению f ( x) f ( x) соответствует равносильное неравенство f ( x) 0