презентация - Уссурийская Астрофизическая Обсерватория
реклама

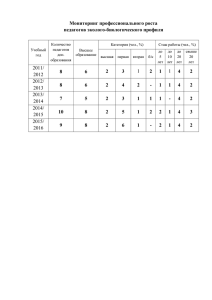
С.Г.Можаровский Об эквивалентности отклика крыльев спектральных линий на малые изменения величин напряженности магнитного поля и лучевых скоростей Уссурийская астрофизическая обсерватория, Россия, Уссурийск, 692533, [email protected] В этой работе мы рассмотрим зависимости изменений профилей [Стокса] спектральных линий от элементарных вариаций физических величин в модели фотосферы В простейшем случае модель фотосферы, это таблица, которая задает распределение с высотой ряда физических величин: T, Pg, Pe , V, B Модель HOLMU Зная модель можно рассчитать профили Стокса фраунгоферовых линий Изучение фотосферы заключается в решении обратной задачи – получении структуры фотосферы из профилей Стокса. Действие на профили разных физических величин запутано, за одни и те же элементарные изменения каждой точки профиля могут отвечать разные величины: температура T, поле скоростей V, магнитное поле B и т.д. Если взять профиль целиком, то можно найти эффективные значения физических величин, усредненные по всему профилю и по всей высоте фотосферы. Например, можно найти: 1. Значение лучевой скорости VLOS по положению центра тяжести всего профиля. 2. Значение продольной компоненты магнитного поля по разности центров тяжести профилей Стокса I+V и I-V. 3. Эффективную температуру по эквивалентной ширине линии W (для линий значительно меняющихся с температурой). Отталкиваясь от этих эффективных значений дальше можно искать распределение физических величин с высотой h. Возьмем для примера лучевую скорость VLOS. Очевидно, что каждая точка бисектора спектральной линии отражает эффективное значение лучевой скорости на некоторой высоте h в фотосфере, значит это распределение можно установить. Такой же образом (как нами было показано в предыдущих работах) можно установить распределение с высотой магнитного поля B. Очевидно, что элементарные изменения лучевой скорости VLOS или напряженности магнитного поля B приводят к элементарным смещениям точек профиля [поглощения] вдоль шкалы длин волн λ. (Для VLOS в одну и ту же сторону для каждого крыла, для B – в разные стороны.) Тогда как изменения температуры T приводят к смещениям точек профиля вдоль шкалы интенсивности I/IC. Можно ли этот факт использовать для разделения информации о влиянии T и о влиянии VLOS и B ? Мы проверили такую возможность расчетами. §1 Связь между элементарными вариациями профиля спектральной линии по оси интенсивностей и по оси длин волн Схема расчетов следующая: 1. Берем одномерную (плоскопараллельную) модель фотосферы. 2. Рассчитаем на её основе профиль спектральной линии (или четверку профилей Стокса, если это необходимо) 3. Задаем малое возмущение интересующей нас физической величины в слое фотосферы толщиной Δh, расположенном на высоте h. 4. Рассматриваем возмущение профиля в каждой его точке в двух разных видах: a) Как изменение элементарной интенсивности ΔI на заданной длине волны λ либо b) как изменение длины волны Δλ участка профиля с заданной интенсивностью I/IC Расчеты показывают, что эти два возмущения - в любой точке профиля линии и - при любой высоте слоя h, к которому приложено возмущение связаны соотношением: ΔI = Δλ∙(dI/dλ), где dI/dλ описывает крутизну крыла в этой точке профиля Таким образом: малое возмущение любой физической величины в модели фотосферы смещает каждый отрезок профиля в направлении перпендикулярном этому отрезку Изменения профиля можно оценивать: - вдоль оси остаточных интенсивностей - вдоль оси длин волн RI λ. Рис. 1. Профиль линии Fe I 6302 Å, использованной для моделирования функций отклика. Для расчета использована модель тени: микротурбулентная скорость: напряженность магнитного поля: угол вектора поля с лучом зрения: Stellmacher & Wiehr 1975, Vmi=0, B=2400 Гс, γ=15°. Выводы к § 1: 1. Сравнивая пару профилей, можно анализировать как разницу ΔI так и Δλ в зависимости от того, что в конкретной ситуации выгоднее. 2. Элементарные изменения в единичной точке профиля линии, вызванные температурой и другими физическими величинами нельзя различить. 3. Следует полагать, что элементарные изменения профиля линии, вызванные изменениями любой из физических величин (T, B, VLOS, …) складываются линейно. По-другому можно сказать так: 4. Для заданной точки профиля линии λ и заданной высоты слоя фотосферы h существуют конкретные отношения приращений физических величин ΔB/ΔVLOS, ΔT/ΔVLOS, ΔT/ΔB, которые дают одинаковый эффект в изменении профиля. § 2 Физический смысл площади под кривой функции отклика RF на возмущение лучевой скорости и магнитного поля Зависимости от высоты h элементарных откликов профиля линии на изменение некоторой физической величины называют функциями отклика (response functions – RF). Рассмотрим конкретный пример • Зададим малое возмущение величине лучевой скорости ΔVLOS = 50 м/с для условной спектральной линии с λ=5000 Å. • Приложим это возмущение ко всей фотосфере (то есть одновременно ко всем её слоям). В результате мы получим смещение всего профиля линии на Δλ = λ∙ΔV/c = 0.833 mÅ. • Приложим возмущение ΔVLOS последовательно к каждому слою фотосферы пробегая высоту h с заданным шагом, например, Δh=10 км. • Фиксируем на профиле линии точку с заданной интенсивностью I/IC, и измерим в этой точке изменение Δλ для каждого значения h. График Δλ(h) и покажет нам функцию отклика RF на возмущение лучевой скорости. Оказывается, что в этом случае, сумма Δλ(h) по всем h составит в точности то же значение 0.833 mÅ. Вывод § 2: Площадь под кривой RF имеет определенный физический смысл. Она равна смещению, которое бы получила точка профиля линии, если бы возмущение было приложено не к набору слоев шириной Δh, а ко всей фотосфере целиком. Модельные расчеты показывают, что тот же вывод справедлив и для вариации магнитного поля B (при условии полного расщепления σ-компонент). Напомним последние выводы из§1 (которые подтверждает§2): 1. Элементарные изменения профиля линии, вызванные изменениями любой из физических величин (T, B, VLOS, …) складываются линейно. Или, что то же самое: 2. Для заданной точки профиля линии λ и заданной высоты слоя фотосферы h существуют конкретные отношения приращений физических величин ΔB/ΔVLOS, ΔT/ΔVLOS, ΔT/ΔB, которые дают одинаковый эффект в изменении профиля. Проверим это эмпирическими расчетами для величин ΔB и ΔVLOS §3 Отношение, описывающее эквивалентное действие возмущений лучевой скорости и напряженности магнитного поля Возьмем для примера спектральную линию Fe I λ 6302 Å. Возмущение магнитного поля ΔB=10 Гс приведет к смещению крыла на величину Δλ=4.67∙10-5∙λ2∙GLande∙ΔB = 0.461 mÅ. Используя соотношение Δλ/λ = ΔV/c можно вычислить, что такое же смещение Δλ дает возмущение ΔV на 21.94 м/с. Построим функции отклика RF на изменения указанных ΔB и ΔV для ряда последовательных значений остаточной интенсивности RI. В расчетах взято большое значение B=3200 Гс с тем, чтобы σ-компоненты были полностью расщеплены. Фрагмент профиля с точками приложения RF Функции отклика RF Совпадение функций отклика по величине и по форме для определенного отношения ΔV /ΔB. Модель HOLMU. Фрагмент профиля с точками приложения RF Функции отклика RF Совпадение функций отклика по величине и по форме для определенного отношения ΔV /ΔB. Модель тени SW75. Таким образом, для каждой магнитоактивной спектральной линии существует отношение, описывающее эквивалентное действие возмущений лучевой скорости и напряженности магнитного поля на крыло: ΔV/ΔB[(м/с)/Гс]=4.6686∙10-13·c·λ·GLande , где c – скорость света, м/с, λ – длина волны спектральной линии, Å, GLande – ее эффективный фактор Ланде. Коэффициенты эквивалентности ΔV/ΔB для ряда спектральных линий Спектральная линия ΔV/ΔB[(м/с)/Гс] Fe I λ 6302 Å 2.19 Fe I λ 6301 Å 1.47 Fe I λ 6336 Å 1.78 Fe I λ 5250 Å 2.20 Fe I λ 5247 Å 1.47 Fe I λ 6173 Å 2.16 Ni I λ 6767 Å 1.35 Повторим выводы работы: 1. Малое возмущение любой физической величины в модели фотосферы смещает каждый отрезок профиля спектральной линии в направлении перпендикулярном этому отрезку. 2. По характеру изменений профиля нельзя разделить физические величины, меняющие длину волны профиля и меняющие интенсивность. 3. Действие на профиль линии возмущений разных физических величин, произошедших на одной и той же высоте складывается линейно. 4. Для каждой точки профиля линии и для каждой высоты элементарного слоя модели существует отношение, которое определяет эквивалентное действие разных величин T, VLOS, B и т.д. Наконец, основной вывод (который соответствует заголовку работы): Функции отклика RF крыльев спектральных линий на возмущения лучевой скорости и абсолютной величины магнитного поля при некотором отношении ΔVLOS/ΔB совпадают по величине и по распределению с высотой (при условии полного расщепления σ-компонент). Возникает вопрос, насколько сильно меняется отношение эквивалентного действия вариаций T и B или T и VLOS - при изменении точки приложения возмущения (т.е. высоты элементарного слоя модели h) - при смене участка профиля (скажем, смещении вдоль оси I/IC). Этот вопрос выходит за рамки данной работы, мы ограничимся небольшой иллюстрацией. Fe I λ 6302 Å, модель HOLMU, B0=2400Гс ΔT=10K, ΔB=10Гс, dh=5км Изменение относительных вкладов T и B с высотой Изменение относительных вкладов T и B с положением на профиле Fe I λ 6302 Å, модель HOLMU, B0=2400Гс ΔT=10K, ΔB=10Гс, dh=5км Изменение относительных вкладов T и B с высотой Изменение относительных вкладов T и B с положением на профиле Выводы работы просты, и можно ожидать, что гденибудь в 40-х годах прошлого века их кто-либо уже публиковал (получив эти выводы не в результате эмпирических модельных расчетов, а в результате аналитических преобразований уравнений переноса). Однако нам не удалось найти ссылок. Спасибо за внимание!