№ Тема Тип урока Элементы
advertisement
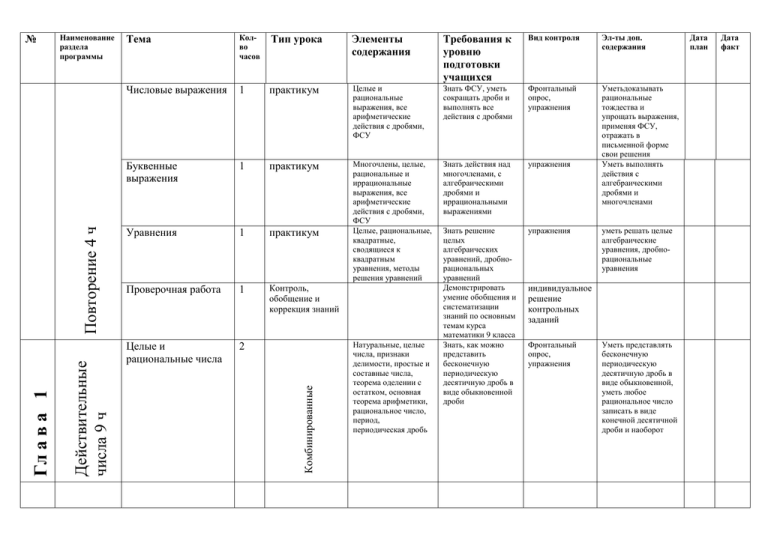
Действительные числа 9 ч Гл а в а 1 Тема Колво часов Тип урока Элементы содержания Требования к уровню подготовки учащихся Вид контроля Эл-ты доп. содержания Числовые выражения 1 практикум Целые и рациональные выражения, все арифметические действия с дробями, ФСУ Знать ФСУ, уметь сокращать дроби и выполнять все действия с дробями Фронтальный опрос, упражнения Буквенные выражения 1 практикум Знать действия над многочленами, с алгебраическими дробями и иррациональными выражениями упражнения Уравнения 1 практикум Многочлены, целые, рациональные и иррациональные выражения, все арифметические действия с дробями, ФСУ Целые, рациональные, квадратные, сводящиеся к квадратным уравнения, методы решения уравнений Уметьдоказывать рациональные тождества и упрощать выражения, применяя ФСУ, отражать в письменной форме свои решения Уметь выполнять действия с алгебраическими дробями и многочленами упражнения Проверочная работа 1 Контроль, обобщение и коррекция знаний Целые и рациональные числа 2 Знать решение целых алгебраических уравнений, дробнорациональных уравнений Демонстрировать умение обобщения и систематизации знаний по основным темам курса математики 9 класса Знать, как можно представить бесконечную периодическую десятичную дробь в виде обыкновенной дроби Комбинированные Наименование раздела программы Повторение 4 ч № Натуральные, целые числа, признаки делимости, простые и составные числа, теорема оделении с остатком, основная теорема арифметики, рациональное число, период, периодическая дробь уметь решать целые алгебраические уравнения, дробнорациональные уравнения индивидуальное решение контрольных заданий Фронтальный опрос, упражнения Уметь представлять бесконечную периодическую десятичную дробь в виде обыкновенной, уметь любое рациональное число записать в виде конечной десятичной дроби и наоборот Дата план Дата факт Действительные числа 1 Бесконечно убывающая геометрическая прогрессия 2 Арифметический корень натуральной степени 3 Степень с рациональным и действительными показателями 3 Контрольная работа №1 1 Действительные числа, числовая прямая, иррациональные числа, бесконечная десятичная периодическая дробь, модуль действительного числа Геометрическая прогрессия, бесконечно убывающая геометрическая прогрессия, знаменатель геометрической прогрессии, формула суммы бесконечно убывающей геометрической прогрессии Арифметический корень натуральной степени, подкоренное выражение, квадратный корень, кубический корень, извлечение корня п-й степени, свойства арифметического корня натуральной степени Степень с любым целочисленным показателем, свойства степени Обобщение и систематизация знаний Знать, как установить, какая из пар чисел образует десятичные приближения для заданного числа, уметь выполнять приближенные вычисления корней Решение упражнений, составление опорного конспекта, ответы на вопросы Уметь решать задачи с целочисленными неизвестными Уметь доказать, что заданная геометрическая прогрессия бесконечно убывающая, уметь находить ее сумму С.р. Уметь решать практические задачи на применение формулы суммы бесконечно убывающей геометрической прогрессии Знать определение корня п-й степени и его свойства, уметь выполнять преобразования выражений, содержащих радикалы, решать простейшие уравнения, содержащие корень п-й степени Знать, как находить значение степени с рациональным показателем, проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени С.р. Уметь применять определение корня пй степени и его свойства, уметь выполнять преобразования выражений, содержащих радикалы, решать уравнения, используя понятие корня п-й степени Уметь обобщать понятие о показателе степени, выполняя преобразования выражений, содержащих радикалы С.р. К.р. 2 Степенная функция, показатель «четное натуральное число», показатель «нечетное натуральное число», показатель «положительное действительное число», показатель «отрицательное действительное число» Взаимно обратные фунцции 2 Монотонные функции, обратимые функции, обратная функция, взаимно обратные функции Равносильные уравнения и неравенства 3 Равносильность уравнений и неравенств, следствие уравнений и неравенств, преобразование данного уравнения в уравнение-следствие, расширение области определения, проверка корней, потеря корней, общие методы Комбинированные Степенная функция 11 ч Глава 2 Степенная функция, ее свойства и график Знать как строить графики степенных функций при различных значениях показателя, уметь описывать по графику, а в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения, уметь строить графики функций Знать, как можно определить взаимно обратные функции, свойство монотонности и симметричности обратимых функций, уметь строить графики взаимно обратных функций, уметь описывать по графику, а в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения Уметь решать простейшие уравнения стандартными методами, уметь решать неравенства с одной переменной, уметь изображать на плоскости множество решений неравенств с одной переменной Пр.р. Знать свойства функций и уметь исследовать функцию по схеме, выполнять построение графиков сложных функций Решение упражнений, ответы на вопросы Уметь найти функцию обратную данной , построить функцию, обратную к заданной, уметь на одном рисунке строить график данной функции и функции, обратной к данной, находить область определения и множество значений каждой из них Фронтальный опрос, упражнения Уметь применять рациональные способы решения уравнений различных типов, самостоятельно искать и отбирать необходимую для решения учебных задач информацию. Уметь свободно решать диофантовое Иррациональные уравнения 4 Иррациональные неравенства 4 Контрольная работа №2 1 Показательная функция, ее свойства и график 2 Показательные уравнения 5 Иррациональные уравнения, метод возведения в квадрат обеих частей уравнения, посторонние корни, проверка корней уравнения, равносильность уравнений, равносильные преобразования уравнений, неравносильные преобразования уравнений Иррациональные неравенства, метод возведения в квадрат обеих частей неравенства, равносильность неравенств, равносильные и неравносильные преобразования неравенств уравнение и систему неравенств с двумя переменными Иметь представление об иррациональных уравнениях и методах их решений, уметь решать простейшие иррациональные уравнения, проверять корни С.р. Уметь решать более сложные иррациональные уравнения, проверять корни, обосновывать отбор Иметь представление об иррациональных неравенствах, о методе решения неравенств, о равносильности неравенств и равносильном преобразовании неравенств С.р. Уметь решать иррациональные неравенства, используя графики функций, методом замены переменной, совершая равносильные перехоы Обобщение и систематизация знаний Комбинированные Показательная функция 9 ч Глава 3 решения уравнений и неравенств К.р. Показательная функция, степень с произвольным действительным показателем, свойства показательной функции, график функции, экспонента, горизонтальная асимптота Иметь представление о показательной функции, ее свойствах и графике, уметь определять значение функции по заданному значению аргумента, строить график функции Пр.р. Показательное уравнение, функциональнографический метод, метод уравнивания Иметь представление о показательном уравнении. Уметь решать простейшие С.р. Знать свойства показательной функции и уметь применять их при решении практических задач творческого уровня, уметь проводить описание свойств показательной функции по заданной формуле без графика Уметь решать показательные уравнения, применяя комбинацию нескольких показательные уравнения и их системы Показательные неравенства 5 Показательные неравенства, методы решения показательных неравенств, равносильность неравенств Иметь представление о показательном неравенстве, уметь решать простейшие показательные неравенства и их системы, использовать для приближенного решения неравенств графический метод С.р. Системы показательных уравнений и неравенств 3 Системы показательных уравнений и неравенств, метод замены переменных, метод умножения уравнений, способ подстановки Знать, как решать системы показательных уравнений и неравенств С.р. Контрольная работа №3 1 Логарифмы 2 Обобщение и систематизация знаний Комбинированный Логарифмическая функция 13 ч Глава 4 показателей, метод введения новой переменной Свойства логарифмов 3 алгоритмов, изображать на координатной плоскости множества решения простейших уравнений и их систем Уметь решать показательные неравенства, применяя комбинацию нескольких алгоритмов, изображать на координатной плоскости множества решения простейших неравенстви их систем Уметьрешитьсистему показательных уравнений и неравенств методом подстановки, методом умножения на число, методом сложения или заменой переменных К.р. Логарифм, основание логарифма, иррациональное число, логарифмирование Уметь устанавливать связь между степенью и логарифмом, понимать их взаимно противоположное значение, вычислять логарифм числа по определению Решение упражнений Свойства логарифмов, логарифм произведения, Знать свойства логарифмов, уметь выполнять арифметические С.р. Знать понятие логарифма, уметь выполнять преобразования логарифмических выражений, вычислять логарифмы чисел, самостоятельно выбирать критерий для сравнения, сопоставления, оценки и классификации объектов Уметь применять свойства логарифмов, на творческом уровне логарифм частного, логарифм степени, логарифмирование 1 Логарифмическая функция, ее свойства и график 2 Логарифмические уравнения 5 Логарифмические неравенства 5 Таблица логарифмов, десятичный логарифм, натуральный логарифм, формула перехода логарифма к другому основанию Логарифмическая функция, логарифмическая кривая, свойства логарифмической функции, график функции Комбинированные Десятичные и натуральные логарифмы Логарифмическое уравнение, потенцирование, равносильные логарифмические уравнения, функциональнографический метод, метод потенцирования, метод введения новой переменной, метод логарифмирования Логарифмическое неравенство, равносильные логарифмические неравенства, методы решения логарифмических неравенств действия, сочетая устные и письменные приемы, находить значение логарифма, проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы Уметь выразить данный логарифм через десятичный и натуральный проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы Ответы на вопросы Уметь строить графики простейших логарифмических функций, уметь находить значение функции при заданном значении аргумента Иметь представление о логарифмическом уравнении, уметь решать простейшие логарифмические уравнения указанными методами Пр.р. Уметь на творческом уровне исследовать функцию по схеме С.р. Уметь решать логарифмические уравнения на творческом уровне, применяя комбинирование нескольких алгоритмов Знать алгоритм решения логарифмического неравенства в зависимости от основания, уметь решать простейшие логарифмические неравенства, применяя метод С.р. Уметь решать простейшие логарифмические неравенства устно, применять свойство монотонности логарифмической функции при решении более сложных неравенств, Контрольная работа №4 1 Обобщение и систематизация знаний Радианная мера угла 1 Поворот точки вокруг начала координат 1 Определение синуса, косинуса и тангенса угла 2 Синус, косинус, тангенс, котангенс и их свойства, четверти окружности Знаки синуса, косинуса и тангенса 2 Знаки синуса, косинуса, тангенса Зависимость между синусом, косинусом и тангенсом одного и того же угла 3 использовать для приближенного решения графический метод К.р. Радианная мера угла, градусная мера угла, перевод радианной меры в градусную, перевод градусной меры в радианную Система координат, числовая окружность на координатной плоскости, координаты точки окружности Комбинированные Тригонометрические формулы 25 ч Глава 5 замены переменных для сведения логарифмического неравенства к рациональному виду Тригонометрические функции числового аргумента, тригонометрические соотношения одного аргумента Уметь выражать градусную меру в радианной и наоборот Ответы на вопросы Уметь находить радианную меру угла, стягиваемого дугой окружности, дугой кругового сектора Знать, как определить координаты точек на числовой окружности, уметь составить таблицу для точек числовой окружности и их координат, по координатам находить точку на числовой окружности Знать понятия синуса, косинуса, тангенса и котангенса произвольного угла, уметь вычислять синус, косинус, тангенс и котангенс числа Знать знаки тригонометрических функций по четвертям Решение упражнений Уметь определять точку числовой окружности по координатам и координаты по точке числовой окружности, находить точки, координаты которых удовлетворяют заданному неравенству Решение упражнений Знать основные тригонометрические тождества, уметь упрощать выражения с применением основных формул, С.р. Уметь, используя числовую окружность, определять синус, косинус, тангенс и котангенс произвольного угла в в радианной и градусной мере Уметь определять знаки тригонометрических функций сложного аргумента, сравнивать значения тригонометрических функций радианной меры угла Уметь упрощать выражения повышенной сложности М.д. Тригонометрические тождества 5 Тождества, способы доказательства тождества, преобразование выражений Синус, косинус и тангенс углов α и – α 2 Формулы сложения 2 Поворот точки на α и –α, определение тангенса, формулы синуса, косинуса и тангенса углов α и -α Формулы синуса и косинуса суммы аргумента, формулы синуса и косинуса разности аргумента Синус, косинус и тангенс двойного угла 2 Формулы двойного аргумента, формулы кратного аргумента Синус, косинус и тангенс половинного угла 2 Формулы половинного угла, формулы понижения степени Формулы приведения 2 Формулы приведения, углы перехода знать, как вывести зависимости между синусом, косинусом и тангенсом одного и того же угла Знать, как доказываются основные тригонометрические тождества, уметь упрощать тригонометрические выражения, используя основные тригонометрические тождества Уметь упрощать выражения, применяя формулы синуса, косинуса и тангенса углов α и -α Знать формулы синуса и косинуса суммы и разности двух углов, уметь преобразовывать простые выражения с помощью этих формул Знать формулы двойного угла, уметь применять их для упрощения выражений С.р. М.д. Уметь упрощать сложные выражения, применяя формулы синуса, косинуса и тангенса углов α и -α М.д. С.р. Уметь выражать функции через тангенс половинного аргумента Знать формулы половинного угла, уметь их применять, уметь понижать степень Знать вывод формул приведения, уметь упрощать выражения с использованием этих формул С.р. 2 Контрольная работа №5 1 Уравнение cos x = a 3 Арккосинус числа, уравнение cos x = a, формула корней уравнения cos x = a Знать формулы для решения уравнения, уметь решать простейшие уравнения С.р. Уравнение Sin x = a 3 Арксинус числа, уравнение Sin x = a, формула корней уравнения Sin x = a Знать формулы для решения уравнения, уметь решать простейшие уравнения С.р. Уравнение Tg x= a 3 Арктангенс и арккотангенс числа, уравнение tg x =a, формула корней уравнения tg x =a Знать формулы для решения уравнения, уметь решать простейшие уравнения С.р. Решение тригонометрических уравнений 6 Уравнения, сводимые к квадратным, замена переменных, уравнение a sinx + b cosx = c, вспомогательный Иметь представление о методе вспомогательного аргумента при решении С.р. Формулы преобразования суммы тригонометрических функций в произведение Уметь преобразовывать суммы тригонометрических функций в произведение, проводить преобразования простых тригонометрических выражений, используя справочную литературу Обобщение и систематизация знаний Комбинированные Тригонометрические уравнения 15 ч Глава 6 Сумма и разность синусов. Сумма и разность косинусов С.р. К.р. Уметь решать простые уравнения методом введения новой переменной и разложением на множители, решать по алгоритму однородные уравнения Уметь решать простые уравнения методом введения новой переменной и разложением на множители, решать по алгоритму однородные уравнения Уметь решать простые уравнения методом введения новой переменной и разложением на множители, решать по алгоритму однородные уравнения Уметь применять метод введения вспомогательного угла 6 Контрольная работа №6 1 Область определения и множество значений тригонометрических функций 2 Четность, нечетность, 2 периодичность тригонометрических функций Свойства функции y= cos x и ее график 2 Свойства функции y = sin x и ее график 2 Свойства функции y = tg x и ее график 2 тригонометрических уравнений Знать, как решаются простейшие тригонометрические неравенства Обобщение и систематизация знаний Комбинированные Тригонометрические функции 12ч Глава 7 Решение простейших тригонометрических неравенств аргумент, уравнения, решаемые разложением левой части на множители Тригонометрическое неравенство, единичная окружность, решение неравенства, множество отрезков С.р. Знать, как решаются более сложные тригонометрические неравенства К.р. Область определения тригонометрических функций, множество значений тригонометрических функций, тригонометрические функции Знать, как определить область определения и множество значений простых тригонометрических функций С.р. Четная и нечетная функции, периодическая функция, период, наименьший положительный период функция y= cos х, ее график, свойства Уметь выяснять четность или нечетность функций С.р. Уметь по схеме описать свойства функции, уметь построить основной график Пр.р. функция y= sin х, ее график, свойства Уметь по схеме описать свойства функции, уметь построить основной график Пр.р функция y= tg х, ее график, свойства Уметь по схеме описать свойства функции, уметь построить основной график Пр.р. Уметь находить область определения и множество значений тригонометрических функций сложного аргумента, представленного в виде дроби и корня Уметь доказывать четность или нечетность функций Уметь свободно строить графики повышенной сложности и описывать их свойства Уметь свободно строить графики повышенной сложности и описывать их свойства Уметь свободно строить графики повышенной сложности и описывать их свойства Обратные тригонометрические функции 2 Контрольная работа №7 1 Итоговое повторение 7 Функции y= arccosx, y = arcsin x, y = arctg x, y = arcctg x, их свойства, графики и соотношения, содержащие арксинус, арккосинус, арктангенс и арккотангенс Обобщение и систематизация знаний Иметь представление об обратных тригонометрических функциях, их свойствах и графиках Пр.р. К.р. Уметь преобразовать выражения, содержащие обратные тригонометрические функции
