файл с задачами по гидростатике
реклама

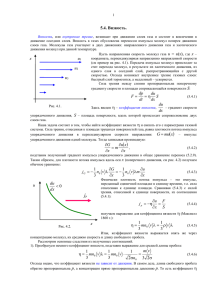
АВТОРЫ ПРОКОФЬЕВА ФЕДОРОВА Тамара Валентиновна Елена Борисовна доцент, к.т.н. ассистент, к.т.н. Методика решения задач по прикладной гидравлике Для студентов ХТФ Задача 1. Определить плотность воздуха при вакууме (разрежении) р = 440 мм рт.ст. и температуре t = - 40ºС. Воздух по объему состоит из 79% азота и 21% кислорода. Давление р0 = 750 мм рт.ст. Решение Мольная масса воздуха: М = 0,79*28 + 0,21*32 = 28,8 кг/кмоль Плотность воздуха при заданных условиях: М 273 р 28 ,8 273750 440 кг 0 ,615 3 22 ,4 Т р0 22 ,4 273 40 750 м Задача 2. Кинематическая вязкость нефти при 20 и 50 ºС составляет: ν20 =0,758 см2/с и ν50=0,176 см2/с. Определить вязкость при t = 105ºС. Решение k lg t1 lg t2 t2 lg t1 0 ,758 t 0 ,758 lg 0 ,176 1 ,595 50 lg 20 105 1 ,595 lg 20 t 0 ,0572 см 2 / с К расчету динамического коэффициента вязкости Для смеси нормальных (неассоциированных) жидкостей значение μсм может быть вычислено по формуле: lgсм x'1 lg 1 x'2 lg 2 где μ1, μ2,...- динамические коэффициенты вязкости отдельных компонентов; х’1, х’2,… - мольные доли компонентов в смеси. В соответствии с аддитивностью текучестей компонентов динамический коэффициент вязкости смеси нормальных жидкостей x v1 x v 2 определяется уравнением: 1 , см 1 2 где xv1, xv2,… - объемные доли компонентов в смеси. Динамический коэффициент вязкости разбавленных суспензий μс может быть рассчитан по формулам: при концентрации твердой фазы менее 10% (об) с ж 1 2 ,5 0 ,59 с ж при концентрации твердой фазы до 30% (об) 0 ,77 2 где μж –динамический коэффициент вязкости чистой жидкости, φ – объемная доля твердой фазы в суспензии. Задача 3. Определить кинематический коэффициент вязкости жидкости, имеющей состав: 70% мол. кислорода и 30% мол. азота при Т=84 К и рабс=1 атм. Считать кислород и азот нормальными жидкостями. Вязкость кислорода: μ1=22,6*10-5 Па*с азота: μ2=11,8*10-5 Па*с Плотность жидкого кислорода: ρ1=1180 кг/м3 азота: ρ2=780 кг/м3 Решение. 1. Динамический коэффициент вязкости для нормальных жидкостей: ' lgсм x1 lg 1 5 lg см 0 ,7 lg 22,6 10 3. 4. ... 0 ,3 lg 11,8 10 5 3,74 см 18 ,2 10 2. ' x2 lg 2 5 Массовые доли компонентов в смеси: 0 ,3 28 0 ,7 32 0 ,273 x1 0 ,727 x2 0 ,7 32 0 ,3 28 0 ,7 32 0 ,3 28 1 3 1035 кг / м Плотность смеси: см 0 ,727 0 ,273 1180 780 Кинематическая вязкость: см см 18 ,2 10 5 0 ,18 10 6 см 1035 Задача 4. ► Вычислить динамический коэффициент вязкости суспензии бензидина в воде, если в чан загружено на 10 м3 воды 1 т бензидина. Температура суспензии 20оС относительная плотность твердой фазы 1,2. Решение. 1. Объем твердой фазы: m 1000 V 0 ,833 м 3 1,2 1000 2. Объемная концентрация твердой фазы в суспензии: 3 0 ,833 м 0 ,077 10 0 ,833 м3 3. При 20оС динамический коэффициент вязкости воды равен 10-3 Па*с или 1 сП. Динамический коэффициент вязкости суспензии определяется по формуле: с ж 1 2 ,5 11 2 ,5 0 ,077 1,19сП 1,19 10 3 Па с или с ж 0 ,59 1 0 ,59 0 ,77 2 0 ,77 0 ,077 2 1,23сП 1,23 10 3 Па с Задача 5. ► Цилиндрический сосуд диаметром 20 см наполнен водой до верха. Определить высоту цилиндра, если сила давления на дно и боковые стенки цилиндра одинакова. ► Решение р0=0 0 ► рбок ► рдн х рбок рср 0 ρgH ► Н/2 Н ► Давление на дно цилиндра одинаково во всех точках и равно рдн р0 gH Давление на стенки цилиндра линейно увеличивается с глубиной рбок р0 gx Значит сила давления на всю боковую поверхность цилиндра равна среднему давлению рср , т.е. давлению на глубине Н/2, умноженному на площадь боковой поверхности: 1 Pбок gH HD 2 Сила давления на дно цилиндра равна D 2 Pдн рдн Fдн gH 4 Из условия равенства сил давления получаем: 1 D D H 10см H 2 2 4 , откуда Задача 6. Вакуумметр на барометрическом конденсаторе показывает вакуум, равный 600 мм рт.ст. Атмосферное давление 748 мм рт.ст. Определить: а) абсолютное давление в конденсаторе в Па и в кгс/см2; б) на какую высоту Н поднимается вода в барометрической трубе? Решение ► Абсолютное давление в конденсаторе: р 748 600 148 ммрт .ст . 148 133,3 19700Па 19700 кгс 2 р 0 , 201 см 9 ,81 10 4 ► Высоту столба в барометрической трубе найдем из уравнения: ратм р gH ► Откуда pатм p 600 133,3 H 8 ,16 м g 1000 9 ,81 Задача 7. ► Тонкостенный цилиндрический сосуд массой 100г и объемом 300см3 ставят вверх дном на поверхность воды и медленно опускают его вглубь таким образом, что он все время остается вертикальным. На какую минимальную глубину надо погрузить стакан, чтобы он не всплыл на поверхность? Атмосферное давление р0=105 Па. Решение ► Воздух в стакане до погружения описывается уравнением состояния Менделеева-Клапейрона: ► После погружения: m p0V0 RT M p1V1 ► m RT M При этом по закону сохранения массы: p0V0 p1V1 ► Давление воды на глубине h: p1 p0 gh уравновешивается давлением воздуха в стакане. ► На стакан со стороны воды действует выталкивающая сила, равная весу стакана в условии равновесия: A G mg в gV1 ► Исходя из вышеперечисленных условий находим глубину h: p1 p0 p0V0 p0 10 5 3 10 4 10 5 h 3 30 10 20 м в g mg g 0 ,1 9 ,8 10 9 ,8 Задача 8. ► Вес камня в воздухе 49Н. Найти вес этого камня в воде, если его плотность равна 2500 кг/м3, а плотность воды 1000 кг/м3. Решение ► ► Из условий равновесия сумма всех сил, действующих на камень, равна нулю: Отсюда: Pвод A Pвод - mg 0 Pвозд А Рвозд mg 0 Pвозд в Рвозд A в gVк в g ► Выталкивающая сила: g к к в 1000 ► Вес камня в воде: Рвод Рвозд 1 49 1 29 ,4 Н к 2500 Задача 9. ►На поверхности воды плавает полый деревянный шар так, что в воду погружена 1/5 часть его объема. Радиус шара 1см. Плотность дерева 840 кг/м3. Найти объем полости в шаре. Решение ► Из условия равновесия: ► Откуда масса шара: A mg в gVпогр m вVпогр V 4r 3 в в 5 53 6 4 3 , 14 10 10 3 8 ,4 10 4 кг 15 ► Объем деревянной части шара: 8 ,4 10 4 6 3 V 10 м д 840 m ► Объем полости: 4 3 4 6 6 V1 V V r V 3 ,14 10 10 3 3 3 10 6 м 3 3см 3