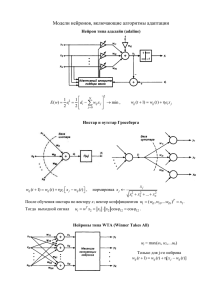
Визильтер Ю.В

Реляционные модели
формы изображений
и метрики их сравнения
Ю.В. Визильтер, А.Ю. Рубис,
[email protected]
Москва, ФГУП «Государственный
научно-исследовательский институт
авиационных систем»
Задача: сравнение изображений по форме
f
g
Насколько похожи ли эти изображения?
Ответ на этот вопрос дает морфология Пытьева, позволяющая
осуществлять сравнение изображений не по яркости, а по форме.
Пытьев Ю.П., Чуличков А.И. Методы морфологического
анализа изображений // М.: ФИЗМАТЛИТ, 2010. 336с.
Задача: сравнение изображения с формой
Морфологические квазирасстояния
Морфологические коэффициенты
корреляции Пытьева:
d M ( g , F )  g  PF g ,
K M ( g , F )  PF g
g ,
d M ( f , G )  f  PG f
K M ( f , G )  PG f
f
В общем случае KM(g,F)KM(f,G).
Это схема яркостногеометрического
сравнения изображений
с формами
f ( x, y)  i 1 fi  Fi ( x, y)
n
Изображения – векторы,
Формы – гиперплоскости.
Задача: сравнение форм
TV
Необходимо перейти от
яркостно-геометрического
сравнения изображений с
формами
к чисто геометрическому
сравнению форм
Контурные методы работают плохо
IR
Нужно определить метрики или меры сходства форм
Компаративная морфология.
В предыдущих работах авторов:
• Предложены меры сходства форм-разбиений на основе
статистического усреднения проецируемых изображений и
получено выражение для среднеквадратичного
эффективного коэффициента морфологической корреляции
форм-разбиений.
• Предложены симметричные нормированные коэффициенты
геометрической корреляции форм-разбиений.
• Предложен способ корреляционного сравнения формразбиений с упорядоченной яркостью.
• Предложено трансформационное расстояние (метрика
редактирования) для оценки геометрических отличий
мозаичных форм (ОГО-метрика).
Трансформационные метрики.
Расстояние Левенштейна
Трансформационное расстояние – минимальная стоимость
цепочки преобразований, переводящей A в B:
ДЫМ  ДЫМА  ДАМА  МАМА
Расстояние Хемминга dH между строками одинаковой длины
определяется как число позиций, в которых символы не совпадают
(равно числу операций замены символа).
Расстояние Левенштейна dL равно минимальному числу операций
для преобразования одной строки в другую, когда множество
элементарных операций состоит из операций вставки, удаления и
замены.
Простейшая метрика сравнения форм-разбиений
на основе слияния-разбиения областей
Структурное расстояние между формами – минимальное число
операций слияния-разбиения, необходимое для перехода от одной
формы другой.
(Контр) Пример сравнения форм при помощи структурного
расстояния редактирования.
Метрика оценки геометрических отличий (ОГО)
d H ( F , G)   j 1 i 1 pij d H (G j , Fi ),
m
n
где n и m – соответствующе количества областей разбиения F и G;
S – площадь кадра ;
pj
Si – площадь области разбиения Fi;
pi
pij
Sj – площадь области разбиения Gj;
Sij – площадь пересечения FiGj;
pi = Si / S – нормированная площадь области разбиения Fi;
pj = Sj / S – нормированная площадь области разбиения Gj;
pij = Sij / S – нормированная площадь пересечения FiGj;
dH(Gj,Fi) = pi + pj – 2pij – нормированное расстояние
Хэмминга между областями разбиения Fi и Gj.
Метрика ОГО как трансформационная метрика
Утверждение. Для любых форм F и G всегда существует такая
проходящая через FG цепочка преобразований w, состоящая из
k элементарных разбиений и l элементарных слияний, причем
сначала следуют все разбиения, а затем все слияния:
F=W0W1…Wk-1Wk=FGWk+1…Wk+l-1Wk+l =G,
для которой справедливо следующее равенство:
d H ( F , G)  t 1 d H (Wt 1 ,Wt )
k l
(Сумма расстояний между последовательными элементами
цепочки равна расстоянию от первого до последнего элемента)
Вывод: Метрика dH(F,G) имеет структуру трансформационного
расстояния с элементарными операциями слияния и разбиения
областей, стоимость которых определяется на каждом шаге
расстоянием dH(Wt-1,Wt) между исходной и получившейся после
данного элементарного преобразования формами.
Свойства метрического пространства с ОГО-метрикой:
геодезические линии не являются единственными
Легко убедиться, что ОГО-метрика не является евклидовой.
Пример пучка геодезических
траекторий, отличающихся
порядком разбиений и слияний
Свойства метрического пространства с ОГО-метрикой:
геодезические многообразия являются дискретными
Иллюстрация
дискретности
геодезических
многообразий в
пространстве
мозаичных форм
на примере
семейства
бинарных форм
dH(F,G) = dH(F,V(x)) + dH(V(x),G) (x-a)2 + (b-x)2 – (b-a)2 = 0 
 x2 – (b+a)x +ba = 0 (x = a ) или (x=b).
Значит, из всех форм семейства V(x) геодезическому многообразию
D(F,G) принадлежат лишь сами формы F=V(a) и G=V(b).
Другой подход:
метрическое сравнение форм
как моделей, описывающих
отношения между элементами
мозаичного изображения
(реляционных моделей)
Предыдущие работы (Источник 1)
В морфологии Пытьева [1] предложена схема описания
формы изображений на основе базисных функций,
связанных с разбиением кадра на непересекающиеся
области. Порождаемые таким образом модели формы
можно назвать T-моделями (Tessellation based shape
models).
f(x,y) = i=1,..,n fi Fi(x,y).
F1
F = { i=1,..,n fi Fi(x,y): fRn}.
1,
 Fi ( x, y)  
 0,
if ( x, y)  Fi ;
otherwise.
F3
F2
Image f(x,y)
F4
Tessellation F
[1] Пытьев Ю.П., Чуличков А.И. Методы морфологического
анализа изображений // М.: ФИЗМАТЛИТ, 2010. 336с.
Предыдущие работы (Источник 2)
В работах [2], [3] был предложен альтернативный способ
описания формы изображений, названных авторами
знаковым представлением изображений и основанный на
рассмотрении множества яркостных отношений между
пикселами изображения, что эквивалентно частично
упорядоченным по яркости T-моделям.
[2] Каркищенко А.Н., Гончаров А.В. Исследование устойчивости
знакового представления изображений // Автоматика и
телемеханика. №9. С. 57-69. 2010.
[3] Броневич А.Г., Гончаров А.В. Аксиоматический подход к
измерению информативности знаковых представлений
изображений // Известия РАН. Теория и системы управления. №6.
C. 206-218. 2010.
Предыдущие работы (Источник 3)
В работе [4] было введено понятие т.н. EMD-метрик*,
используемых для сравнения «гистограммоподобных»
описаний, представленных конечным множеством пар
<Fi,hi>, где Fi – i-й «объект» описания, а hi – его «вес»
(значимость в описании):
d EMD ( F , G)  min( hij ) j 1 i 1 hij d E ( Fi , G j )
m
n
Здесь dE – базовая (Earth) метрика, а веса удовлетворяют
условиям:

m
j 1
h j  1,

n
  h
  h , h 
h  1,
i 1 i
i, j : hij  0, Si
m
n
j 1
i 1 ij
m
j 1 ij
n
j
1
h
i 1 ij
[4] Y. Rubner, C. Tomasi, and L. J. Guibas. “The Earth Mover’s
Distance as a Metric for Image Retrieval”, International Journal of
Computer Vision, 40(2):99-121, 2000.
*Частный случай метрик Монжа-Канторовича
Предыдущие работы (Источник 3)
d EMD ( F , G)  min( hij ) j 1 i 1 hij d E ( Fi , G j )
m
n
hi
i
hij
hj
Оптимизация
«перевозок» весов из
гистограммы в
гистограмму =
«Транспортная задача»
j
Задача решается методом линейного программирования
В данной работе (анонс результатов):
1. Для рассмотрения произвольных типов отношений
между областями разбиения кадра (не только по
яркости, но и по размеру, по форме, по текстуре, по
взаимному расположению и т.п.) будет определен
более общий класс реляционных моделей формы
изображений или TR-моделей (Tessellation based
Relational shape models).
2. Будет описан формализм TR-моделей и показаны
перспективы их практического применения в задаче
сравнения изображений по форме.
3. Будет показано, что метрики сравнения TR-моделей
представляют собой специальный класс EMD-метрик,
который предлагается называть RMD-метриками.
Морфология Пытьева. Описание форм
Множество изображений одной формы разбиения кадра F –
выпуклое и замкнутое подпространство FL2():
F  { f ( x, y)  i 1 f i  Fi ( x, y), f  R }
n
n
Для любого изображения g(x,y)L2() может быть определена
проекция на форму F:
g F ( x, y )  PF g ( x, y )  i 1 g Fi  i ( x, y ),
n
g Fi  (  Fi , g )  Fi , i  1, , n
2
PF – оператор проекции или проектор на F.
Формы – замкнутые и выпуклые подпространства
линейного пространства изображений.
Морфология Пытьева. Сложность форм
Формы-разбиения частично
упорядочены по сложности:
Для любых форм F и G
можно указать форму более
сложную FG и менее
сложную FG.
• Более сложные формы
получаются из менее
сложных разбиением,
• Менее сложные из более
сложных – слиянием
областей.
Альтернативное описание форм отношениями пикселов
Введем предикат бинарного отношения пикселов «равно/неравно
по яркости»:
1, если f ( x, y )  f (u, v);
 F ( x, y , u , v )  
0, если f ( x, y )  f (u, v).
Определим L1-норму TR-формы F(x,y,u,v):
 F       F ( x, y, u, v) dx dy du dv.
Пусть изображения из F и G имеют вид
f ( x, y )  i 1 f i  Fi ( x, y ),
n
g ( x, y )   j 1 g j  Gj ( x, y )
m
тогда
0, если i :  Fi ( x, y )   Fi (u, v);
 F ( x, y , u , v )  
1, в противном случае,
0, если j :  Gj ( x, y )   Gj (u, v);
 G ( x, y , u , v )  
1, в противном случае,
то есть TR-формы будут кусочно-постоянными 4D функциями.
Альтернативное описание форм отношениями областей
Рассмотрим форму W = F  G с областями Wij = Fi  Gj. Для нее
можно записать
0, если i  k , Wij ,Wkl  Fi ;
 F (Wij ,Wkl )  
1, в противном случае,
0, если j  l , Wij ,Wkl  G j ;
 G (Wij ,Wkl )  
1, в противном случае,
Любые операции над T-формами F и G могут быть описаны в
терминах операций над такими бинарными матрицами размера
(mn)2. В частности
 F   j 1 i 1 l 1 k 1 Sij Skl F Wij ,Wkl ,
m
n
m
n
где Sij, Skl – площади областей разбиения Wij,Wkl.
Матрицы отношений "равно/неравно" для 1D-функций
f
g
SF1 SF2
0
F =
1
1
SF3
1
1
0
1
1
0
G =
SG1
SG2
0
1
1
0
Описание форм с упорядоченной яркостью пикселов
Для описания форм-разбиений с частично упорядоченной
яркостью введем векторный бинарный предикат =1,2 для
описания всех возможных отношений упорядоченности по
яркости «пикселы больше/меньше/равны/неравны по яркости»:
 0,0 , если f ( x, y )  f (u , v);

 1,0 , если f ( x, y )  f (u , v);
τ F ( x, y , u , v )  
 0,1 , если f ( x, y )  f (u , v);
 1,1 , если f ( x, y )  f (u , v).

Значение 1,1 означает, что данная пара пикселов в данной форме
F не упорядочена по яркости. Определим L1-норму TR-формы
F(x,y,u,v):
τ F      τ F ( x, y, u, v) dx dy du dv,
где | F(x,y,u,v) | = F(x,y,u,v)1 + F(x,y,u,v)2.
Описание форм с упорядоченной яркостью пикселов
Пусть изображения из F и G имеют вид кусочно-постоянных
функций, причем все значения {fi} являются различными, как и все
значения {gj}. Тогда
 0,0 , если i :  Fi ( x, y )   Fi (u , v);

 1,0 , если i, k :  Fi ( x, y )   Fk (u , v)  1, f i  f k ;
τ F ( x, y , u , v )  
 0,1 , если i, k :  Fi ( x, y )   Fk (u , v)  1, f i  f k ;
 1,1 , в противном случае,

 0,0 , если j :  Gj ( x, y )   Gj (u, v);

 1,0 , если j , l :  Gj ( x, y )   Gl (u , v)  1, g j  g l ;
τ G ( x, y , u , v )  
 0,1 , если i, k :  Gj ( x, y )   Gl (u , v)  1, g j  g l ;

 1,1 , в противном случае,
Описание форм с упорядоченной яркостью областей
Следовательно, такие TR-формы также можно записать в виде
векторных бинарных матриц размера (mn)2:
f ( x, y )  i 1 f i  Fi
n
 0,0 , если i  k , Wij , Wkl  Fi ;

 1,0 , если f i  f k ;
τ F (Wij , Wkl )  
 0,1 , если f i  f k ;
 1,1 , в противном случае ,

( x, y ),
g ( x, y )   j 1 g j  Gj ( x, y )
m
Выражение для L1-нормы:
 0,0 , если j  l , Wij , Wkl  G j ;

 1,0 , если g j  g l ;
τ G (Wij , Wkl )  
 0,1 , если g j  g l ;

 1,1 , в противном случае.
τ F   j 1 i 1 l 1 k 1 Sij S kl  F Wij ,Wkl 1   F Wij ,Wkl 2 .
m
n
m
n
Матрицы отношений "больше" для 1D-функций
f
g
SF1 SF2
0
1F =
0
1
SF3
1
0
0
0
1
0
SG1
SG2
0
1
0
0
1G =
Матрицы отношений "меньше" для 1D-функций
f
g
SF1 SF2
2F =
SF3
0
0
1
1
1
1
0
0
0
SG1
SG2
0
0
1
0
2G =
Описание форм-разбиений произвольными отношениями
Обобщение 1. Пусть дано некоторое изображение f(x,y) и некоторый
упорядоченный набор (вектор) r функций отношения
TR(a,b): R2R, t = 1,…,p.
R-моделью изображения f по набору отношений r между пикселами
назовем векторную функцию
ρ F ( x, y, u, v)  TR( f ( x, y ), f (u, v)) t 1
TR-моделью изображения f формы F по набору отношений r между
областями разбиения назовем векторную матрицу
p
ρ F ( Fi , Fk )  TR( f ( x, y ), f (u, v) : ( x, y )  Fi , (u, v)  Fk ) t 1.
При сравнении TR-моделей изображений f и g формы F и G
соответственно, TR-модели F(Fi,Fk) и G(Gj,Gl) эквивалентно
преобразуются к виду F(Wij,Wkl) и G(Wij,Wkl), где Wij = Fi  Gj.
При этом L1-норма обобщенной TR-модели F(x,y,u,v) определяется
m
n
m
n
p
выражением
ρ F   j 1 i 1 l 1 k 1 Sij Skl t 1  Ft (Wij ,Wkl ) .
p
L1-метрика в пространстве T-моделей
Рассмотрим расстояние Хэмминга (L1-метрику) между формамиотношениями «равно/неравно по яркости» F(x,y,u,v) и G(x,y,u,v):
d ( F , G)   F ( x, y, u, v)   G ( x, y, u, v) 
      F ( x, y, u, v)   G ( x, y, u, v) dx dy du dv
(1)
Для кусочно-постоянных функций выражение (1) можно
преобразовать к виду
d ( F , G)   j 1 i 1 l 1 k 1 Sij S kl  F (Wij ,Wkl )   G (Wij ,Wkl ) ,
m
n
m
n
где Sij, Skl – площади областей Wij,Wkl, причем
0, если  F (Wij ,Wkl )   G (Wij ,Wkl );
 F (Wij ,Wkl )   G (Wij ,Wkl )  
1, в противном случае.
L1-метрика T-моделей и ОГО-метрика
Введем обозначение
1, если i  k , j  l или i  k , j  l ;
 (i, j, k , l )  
0, в противном случае.
Тогда
d ( F , G)   j 1 i 1 l 1 k 1 Sij S kl  (i, j, k , l ) 
m
n
m
n
  j 1 i 1 Sij ( Si  S j  2Sij ),
m
n
где Si и Sj – площади областей Fi и Gj.
Таким образом, при S=1 мы получаем метрику оценки
геометрических отличий (ОГО-метрику) для T-форм F и G:
d ( F , G)   j 1 i 1 Sij d H ( Fi ,G j ),
m
n
(2)
где dH(Fi,Gj) = Si + Sj – 2Sij – расстояние Хэмминга (L1-метрика)
между парами областей Fi и Gj.
L1-метрика отношений "равно/неравно" для 1D-функций
f
g
SF1 SF2
0
F =
1
1
SF3
1
1
0
1
1
G =
0
| F - G | =
0 1
1 0
0 1
1
1
0
0
0 0
1
0
SG1
SG2
0
1
1
0
0
1
d ( F , G)   j 1 i 1 l 1 k 1 Sij S kl  F (Wij ,Wkl )   G (Wij ,Wkl )
m
n
m
n
L1-метрики в пространстве TR-моделей
Аналогичным образом можно ввести L1-метрику для сравнения
«знаковых представлений»:
d ( F , G)  τ F ( x, y, u, v)  τ G ( x, y, u, v) 
  j 1 i 1 l 1 k 1 Sij S kl t 1  Ft Wij ,Wkl    Gt Wij ,Wkl .
m
n
m
n
2
(3)
Обобщение 2. В общем случае для сравнения TR-моделей можно
ввести L1-метрику вида
d  ( F , G)  ρ F ( x, y, u, v)  ρG ( x, y, u, v) 
  j 1 i 1 l 1 k 1 Sij S kl t 1  Ft Wij ,Wkl    Gt Wij ,Wkl .
m
n
m
n
p
(4)
L1-метрики отношений "больше" для 1D-функций
f
g
SF1 SF2
0
1F =
0
1
SF3
1
0
0
0
1
SG2
0
1
0
0
1G =
0
| 1F - 1G | =
SG1
0 1
0 0
0 0
0
1
0
1
1
0
1 1
1
0
L1-метрики отношений "меньше" для 1D-функций
f
g
SF1 SF2
2F =
SF3
0
0
1
1
1
1
0
0
SG2
0
0
1
0
2G =
0
| 2F - 2G | =
SG1
0 0
1 1
0 0
0
1
1
1
1
1
1 1
0
0
Метрики сравнения TR-моделей как EMD-метрики
EMD-метрики используются для сравнения «гистограммоподобных» описаний, представленных конечным множеством пар
<Fi,hi>, где Fi – i-й «объект» описания, а hi – его «вес» (значимость
в описании):
d EMD ( F , G)  min( hij ) j 1 i 1 hij d E ( Fi , G j ),
m
n
(5)
Здесь dE – базовая (Earth) метрика, а веса удовлетворяют
условиям:

m
j 1
 
 0, h   h , h  
h j  1,
i, j : hij

n
h  1,
i 1 i
m
i
j 1 ij
m
n
j 1
i 1 ij
n
j
h  1,
h.
i 1 ij
При выборе в качестве «объектов» элементарных областей Fi и Gj,
в качестве их «весов» hi = Si / S, hj = Sj / S, hij = Sij / S, а в качестве
базовой метрики расстояния Хэмминга dH(Fi,Gj), EMD-метрика (5)
превращается в ОГО-метрику (2).
Метрики сравнения TR-моделей как EBD-метрики
Назовем EBD-метрикой сравнения форм-разбиений (Earth Based
Shape Distance, EBSD-метрика) метрику следующего вида:
d ESMD ( F , G)   j 1 i 1 Sij d E ( Fi , G j ),
m
n
(6)
где dE(Fi, Gj) – любая базовая (Earth) метрика dE, позволяющая
попарно сравнивать какие-либо характеристики областей Fi и Gj.
В частности, для сравнения форм-разбиений с частично или
полностью упорядоченной яркостью определим
d ( Fi , G j )  l 1 k 1 S kl τ F Wij ,Wkl   τ G Wij ,Wkl  ,
(7)
d ( F , G )   j 1 i 1 Sij d ( Fi , G j ).
(8)
m
m
n
n
EBD-метрика (8) эквивалентна ранее введенной L1-метрике (3).
RBD-метрики для сравнения форм-отношений
Обобщение 3. EBD-метрики второго порядка вида
d ( F , G)   j 1 i 1 l 1 k 1 Sij S kl d (ρ F (Wij ,Wkl ),
m
n
m
n
ρG (Wij ,Wkl )),
(9)
где d(F(Wij,Wkl), G(Wij,Wkl)) – предбазовая метрика
сравнения отношений предлагается называть RBDметриками (Relation Based Distance).
RMD-метрики и задачи оптимизации RBD-метрик
Обобщение 4. Если значения Sij трактовать не как набор площадей
пересечения областей кадра фиксированной геометрии, а как
набор переменных мер соответствия между элементами
обобщенной реляционной модели формы, то для определения
RMD-метрики (Relation EMD) необходимо решать
оптимизационную задачу следующего вида:
d ( F , G)   j 1 i 1 l 1 k 1 Sij S kl d (Wij ,Wkl ) 
m
n
m
n
 min( Sij  var, Si , S j  const),

m
S

S
,
j
j 1

n
S

S
,
i
i 1
i, j : Sij  0, Si   j 1 Sij
m
 
, S 
m
j 1
n
S

S
,
ij
i 1
n
j
(10)
i 1
Sij .
Это задача квадратичного программирования, разрешимая по КунуТакеру.
Потенциальные области применения
• Сравнение моделей сегментированных изображений
сцен с наборами пространственных и семантических
отношений между объектами;
• Сравнение описаний формы сегментированных 2D и
3D фигур с наборами топологических,
геометрических и других отношений между частями
фигур;
• Сравнение результатов классификации и
кластеризации в многомерных пространствах
признаков в задачах машинного обучения.
• Сравнение теорий (онтологий), описывающих
единую предметную область.
Сравнение моделей сегментированных изображений сцен
с наборами пространственных и семантических отношений
между объектами
1
1. Сохранены площади, относительные ориентации и расположения
2
2. Сохранены относительные расположения
3
3. Сохранены только площади
Сравнение описаний формы сегментированных 2D и 3D фигур
с наборами топологических, геометрических и других отношений
между частями фигур
Сравнение результатов классификации и кластеризации
в многомерных пространствах признаков
в задачах машинного обучения
fX
fX
gX
gX
FX
X
GX
X
Заключение
1. В работе предложен обобщенный класс моделей описания
формы сегментированных изображений набором
произвольных отношений между областями разбиения
кадра – TR-модели (Tessellation based Relational shape
models).
2. Показано, что получаемые на основе TR-моделей метрики
сравнения форм в общем случае представляют собой
специальный класс EMD-метрик второго порядка, который
предложено называть RMD-метриками (Relation Moving
Distance).
3. Возможные направления дальнейших исследований могут
быть связаны с построением конкретных прикладных
RMD-метрик, а также с построением RMD-метрик для
сравнения предметных онтологий (онтологических
метрик).
Литература
[1] Пытьев Ю.П., Чуличков А.И. Методы морфологического анализа
изображений // М.: ФИЗМАТЛИТ, 2010. 336с.
[2] Каркищенко А.Н., Гончаров А.В. Исследование устойчивости
знакового представления изображений // Автоматика и телемеханика. №9.
С. 57-69. 2010.
[3] Броневич А.Г., Гончаров А.В. Аксиоматический подход к измерению
информативности знаковых представлений изображений // Известия РАН.
Теория и системы управления. №6. C. 206-218. 2010.
[4] Y. Rubner, C. Tomasi, and L. J. Guibas. “The Earth Mover’s Distance as a
Metric for Image Retrieval”, International Journal of Computer Vision,
40(2):99-121, 2000.
[5] Визильтер Ю.В., Рубис А.Ю. Морфологические коэффициенты
корреляции форм изображений для задач комплексирования
многоспектральной видеоинформации // Вестник компьютерных и
информационных технологий, N3, 2012, с.14-20.
[6] H. Ling and K. Okada. “EMD-L1: An Efficient and Robust Algorithm for
Comparing Histogram-Based Descriptors”, European Conference on Computer
Vision (ECCV), LNCS 3953, III:330-343, 2006.