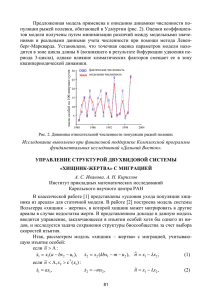
Взаимодействие между потребителями и их пищей («потребитель-корм», или «хищник-жертва») и
реклама

Взаимодействие между потребителями и их пищей («потребитель-корм», или «хищник-жертва») и энергетический бюджет организма «Понятие связи хищник-жертва применяется в экологии по отношению не только к таким бесспорным хищникам и их жертвам как лев и [антилопа-] гну или щука и плотва, но также и к таким как большая синица и насекомые, плотва и планктонные рачки дафнии, дафния и одноклеточные водоросли или даже гну и травянистые растения. Таким образом, в широком смысле слова отношения хищник-жертва охватывают все взаимодействия, при которых одни организмы используют в пищу другие. Очевидно, взаимосвязи паразитов с хозяевами также попадают в разряд отношений хищник-жертва … [«Жертва»] может быть и неживой, например, опавшие листья, поедаемые дождевыми червями, или ионы фосфора, потребляемые растениями.» (А.М. Гиляров. Популяционная экология. 1990, с. 125) Первый вопрос, который необходимо рассмотреть в рамках взаимоотношений между потребителем и его пищей (или, по-другому, между хищником и жертвой), - это вопрос о потреблении пищи и путях расходования потребленной энергии в организме Этот блок лекций, наряду с количественной характеристикой скорости потребления пищи, включает также совокупность вопросов, связанных с расходом энергии, потребленной с пищей. Эта энергия расходуется на такие важные в экологическом отношении функции организма как поддержание жизнедеятельности («траты на обмен», или «дыхание»), рост (соматическая продукция) и размножение (генеративная продукция). В совокупности эти траты составляют энергетический бюджет организма. Потребление пищи и ее расходование в организме потребителя («хищника») – энергетический бюджет (или баланс энергии) организма «Дерево энергетических трат» Прирост структурной массы* Прирост запасных питательных веществ Pg Соматическая продукция, Ps Продукция, P Ассимилированная (т.е. усвоенная) пища, или ассимилированная энергия, или просто ассимиляция, A Ps Генеративная продукция, Pg P T A Траты на обмен, T U Неассимилированная пища (энергия), U C Потребленная пища (рацион), C * Прирост структурной массы – это увеличение массы, связанное с увеличением размера организма «в длину», то есть это рост в узком смысле; в отличие от этого, прирост запасных питательных веществ – это увеличение массы, которое, как правило, не связано с увеличением «длины» организма, а связано только с накоплением запасных веществ Система экологических коэффициентов («экологические эффективности») Стандартные коэффициенты Усвояемость (эффективность ассимиляции) A C Коэффициент использования потребленной пищи на рост, коэффициент K1 В.С. Ивлева P K1 C Коэффициент использования усвоенной пищи на рост, коэффициент K2 В.С. Ивлева P K2 A Нестандартный коэффициент (который пригодится нам в дальнейшем) Коэффициент использования потребленной пищи на генеративную продукцию Pg C Соотношение между коэффициентами K1 K2 С помощью этого и других аналогичных соотношений можно переходить от одних компонентов энергетического бюджета к другим (см. следующий слайд) «Дерево энергетических трат» очевидным образом ведет к пирамиде продукций – соотношению продукций последовательных трофических уровней. Тем самым от экологии взаимодействующих популяций мы переходим к экологии сообществ и экосистем Применение экологических коэффициентов Известно, как траты обмен зависят от массы тела. Например, для млекопитающих эта зависимость передается уравнением (см. следующий слайд) T = 288 W0.76 , где T измеряется в кДж/сут, а W в кг. Поэтому зная массу тела, можно рассчитать траты на обмен. Теперь воспользуемся равенством A=P+T и подставим его в уравнение для K2 K2 = P/A = P/(P + T) , откуда P = [K2/(1 – K2)]*T. (проверьте!) Таким образом, зная T и K2, можно найти продукцию P. Далее, зная продукцию и траты на обмен, можно найти ассимиляцию A = P + T, а зная ассимиляцию и коэффициент α, можно найти потребление (рацион) C = A/α. Таким образом, зная только массу тела, можно найти все компоненты энергетического бюджета! Помните, однако, что это несколько обманчивая простота, поскольку в этих расчетах мы используем экологические коэффициенты как физические константы. На самом же деле экологические коэффициенты зависят от условий и, если нам нужны надежные оценки C, A, P и T, должны быть измерены в каждой конкретной ситуации. Траты на обмен – зависимость обмена от массы тела (эта зависимость уже была рассмотрена в одной из предыдущих лекций) Зависимость скорости основного обмена T (кДж/сут) (на рисунке обмен обозначен R) от массы тела W (кг) для млекопитающих и птиц («кривая от мыши до слона») T = 288 W0.76 Источник : Гильманов Г.Г. 1987. Введение в количественную трофологию и экологическую биоэнергетику наземных позвоночных, с. 32, рис. 4. Исходный источник: Benedict F.G. 1938. Vital Energetics: A Study in Comparative Basal Metabolism. Carnegie Institution of Washington, Washington, DC. Рацион и его зависимость от концентрации пищи Количественной мерой скорости потребления пищи является рацион. Рацион – это количество пищи, потребленной одной особью потребителя («хищника») в единицу времени, или по-другому скорость потребления пищи (скорость потребления «жертв») потребителем Зависимость рациона от концентрации пищи называется функциональной реакцией (functional response). Этот термин обычно используют при описании взаимодействия «хищник-жертва». Если же изучают питание как таковое, то обычно говорят просто о зависимости рациона от концентрации пищи. Три типа функциональной реакции по Холлингу (Holling 1959) Тип III Рацион Тип II Рацион Рацион Тип I Концентрация пищи (или плотность жертв), R Рацион Функциональная реакция первого типа Тип I Cmax – максимальный рацион Cmax Концентрация пищи, R RL Начальная лимитирующая концентрация RL (incipient limiting concentration). Вопросы: (1) как изобразить эту концентрацию в пространстве ниши? (2) Как она соотносится с пороговой концентрацией? (3) Как изменится уравнение (1) и как будет выглядеть зависимость рациона от концентрации пищи, если существует такая концентрация, что ниже ее рацион равен нулю? T – время поиска одной жертвы при концентрации пищи R 1 T aR (1) Чем больше концентрация, тем меньше время поиска; в этой модели предполагается, что время поиска в точности обратно пропорционально концентрации пищи. Размерность коэффициента a [a] = [время]-1 × [концентрация]-1 Зависимость рациона от концентрации пищи (сколько жертв поймает хищник в единицу времени) 1 C aR T C =aR при R < RL C = Cmax = const при R > RL Зона толерантности по F2 Фактор F2 (н-р, температура) Как изобразить начальную лимитирующую концентрацию в пространстве ниши и как она соотносится с пороговой концентрацией Начальная лимитирующая концентрация приблизительно определяет левую границу зоны оптимума для концентрации пищи Начальная лимитирующая концентрация RL Зона толерантности по R Концентрация пищи R Зона оптимума по R Пороговая концентрация R* Почему такое представление RL является приблизительным? Потому что пространство ниши определяется на основе свойств популяции: в области ниши скорость популяционного роста r ≥ 0. Пороговая концентрация пищи R* также определяется на основе свойств популяции: при R > R* скорость популяционного роста r > 0. Однако начальная лимитирующая концентрация RL определяется на основе свойств особи, т.к. функциональная реакция – это характеристика особи (одной особи потребителя). Величины RL для особей разного возраста могут быть разными (по мере роста особи могут переходить с одного вида пищи на другой!), поэтому трудно говорить о зоне оптимума для популяции, исходя из начальной лимитирующей концентрации для особей. Зависимость рациона от концентрации жертв при наличии убежищ для жертв Рацион Функциональная реакция 1-го типа при условии, что существует такая концентрация пищи R0, что ниже ее рацион равен нулю. Это можно интерпретировать как наличие убежищ для жертв. Фактически это означает, что при R < R0 организм не питается данным видом корма. Небольшое изменение делает уравнение гораздо более реалистичным! T – время поиска одной жертвы при концентрации пищи R 1 T a ( R R0 ) Чем больше концентрация, тем меньше время поиска; в этой модели предполагается, что время поиска обратно пропорционально разности между текущей концентрацией и минимальной концентрацией R0. При R = R0 время поиска равно бесконечности. Вопрос: Как в этом случае выглядит график зависимости времени поиска T от R? Cmax Зависимость рациона от концентрации пищи (сколько жертв поймает хищник в единицу времени) RL R0 Концентрация пищи, R R0 – это тоже пороговая концентрация. Но так ее лучше не называть или называть с соответствующими оговорками, поскольку термин «пороговая концентрация» уже занят. 1 C a ( R R0 ) T C = a (R – R0) при R0 < R ≤ RL C = Cmax = const при R > RL Пороги бывают разные … Популяционная пороговая концентрация пищи С одним типом пороговой концентрации пищи мы уже знакомы – это такая концентрация, при которой рождаемость потребителя равна его смертности, так что скорость роста численности r равна нулю и численность постоянна. Это популяционная пороговая концентрация пищи («пороговая концентрация по r»). Ниже этой концентрации популяция не может существовать. Удельная скорость роста r Удельная смертность m Удельная рождаемость b Временной ход обилия потребителя и ресурса r Популяционная пороговая концентрация пищи R* Чем ниже пороговая концентрация, тем больше вид устойчив к недостатку пищи. В теории жизненных стратегий РаменскогоГрайма такие виды называются патиентами (или стресстолерантами). Пороги бывают разные … Индивидуальная пороговая концентрация пищи Ассимиляция / Дыхание / Прирост Индивидуальная пороговая концентрация пищи («пороговая концентрация по приросту») – это такая концентрация, при которой поступающей с пищей энергии («ассимиляция») хватает только на то, чтобы покрыть траты организма на поддержание жизнедеятельности (на «дыхание» или «обмен»). Ниже этой концентрации организм не может существовать. При такой концентрации организм может существовать, но не может расти и размножаться. Ассимиляция (α × Рацион) Дыхание (траты на обмен) Все эти характеристики относятся к особи! Прирост и размножение 0 Концентрация пищи R В этом диапазоне концентрации пищи организм растет и размножается Индивидуальная пороговая концентрация (при такой концентрации прирост равен нулю) Вопрос: Как соотносятся между собой индивидуальная и популяционная пороговая концентрации? Какая из них выше? Ответ: Выше популяционная. Почему? Подсказка: примите во внимание наличие смертности Обратите внимание: дыхание не равно нулю даже при голодании! Источник: Lampert W., Sommer U. 2007. Limnoecology (с изменениями) α = const – коэффициент ассимиляции Функциональная реакция второго типа («уравнение дисков» Холлинга) Рацион Cmax Тип II Cmax/2 Cmax = 1/h R = 1/ah Концентрация пищи, R aR C 1 ahR По сравнению с уравнением, приведшем к уравнению для функциональной реакции первого типа, вводится новый параметр, время «обработки» жертвы (handling time), h. (Время обработки можно интерпретировать как собственно время потребления одной жертвы.) Тогда отрезок времени между захватом одной жертвы и захватом следующей равен времени поиска одной жертвы при концентрации пищи R (T = 1/aR) плюс время обработки h 1 T h h aR Зависимость рациона от концентрации пищи (сколько жертв поймает хищник в единицу времени) в этом случае такова: Чем отличается уравнение для реакции 2-го типа от уравнения для реакции 1-го типа? Тем, что уравнение 2-го типа естестh венным образом описывает выход рациона на плато, тогда как в уравнении 1-го типа выход на плато задается искусст- График этой функции имеет вид, характерный для функциональной реакции второго типа. (Почему?) венно 1 1 aR C 1 T 1 ahR h aR Между прочим, «уравнение дисков» Холлинга уже встречалось в нашем курсе. Это то же самое, что уравнение Моно! Сравните: Уравнение Холлинга (Holling 1959) для зависимости рациона от концентрации пищи (функциональная реакция 2-го типа) aR C 1 ahR Уравнение Моно (Monod 1950) или, что то же самое, уравнение Михаэлиса-Ментен, использованное Тильманом в его ресурсной теории конкуренции для описания зависимости удельной рождаемости водорослей от концентрации биогенов (см. лекции 14-18). В теории взаимодействия хищник-жертва это уравнение называют численной реакцией (хищника на жертву) Это одно и то же уравнение! b bmax R kR Казалось бы, разные по смыслу процессы, а описываются одним и тем же уравнением. Такое, конечно, бывает, однако в этом случае всегда задаешься вопросом: а на самом ли деле эти процессы разные? Обратимся к «дереву энергетических трат». Pg непосредственно связана с b: Pg = w0*b, где w0 - масса новорожденной особи. С помощью введенного нами коэффициента β величина Pg связана с рационом C: β = Pg/C. Таким образом, между b и C имеется прямая пропорциональность, b = (β/w0)*C, конечно, при условии, что β = const. Уравнение В.С. Ивлева для зависимости рациона от концентрации пищи Пример функциональной реакции 2-го типа дают опыты В.С. Ивлева, однако В.С. Ивлев для описания зависимости рациона от концентрации пищи использовал другое уравнение C – рацион потребителя, R – концентрация пищи dC (Cmax C ) dR d [ln( Cmax C )] d (R) dC dR Cmax C ln( Cmax C ) |C0 R |0R d (Cmax C ) dR Cmax C d [ln( Cmax C )] d (R) C R 0 0 Cmax C ln( ) R Cmax Cmax C Cmax e R Уравнение Ивлева C Cmax (1 e R ) Виктор Сергеевич Ивлев и его знаменитая книга (1955) В.С. Ивлев (1907-1964) Обложка переиздания 1977 г. Зависимость рациона от концентрации пищи (Ивлев 1955) Карп Cyprinus carpio http://fish.krasu.ru Вобла Rutilus rutilus caspicus http://sumskoyclub.ru Уклея Alburnus alburnus http://www.poplavok -kiev.narod.ru Характеристика опытов – Уравнение Ивлева C Cmax (1 e R ) Источник: В.С. Ивлев. Экспериментальная экология питания рыб. М. 1955 (цитируется по изданию 1977 г.) вид зависимости не зависит от типа корма Корм – бентос Корм – планктон Функциональная реакция третьего типа Рацион Тип III Функциональная реакция 3-го типа передается S-образной зависимостью. Эта зависимость характерна для позвоночных хищников, которые либо переключаются на новый вид жертв, когда он становится более обычным, либо постепенно научаются ловить свою жертву по мере роста ее численности. Концентрация пищи, R Функциональная реакция третьего типа может быть описана следующим уравнением Сравните уравнение для функциональной реакции 3-го типа с уравнением для реакции 2-го типа. Как сразу увидеть, что уравнение 3-го типа имеет S-образную форму? aR C 1 ahR Обратите внимание: Одна и та же зависимость (в данном случае Sобразная зависимость рациона от концентрации пищи) может быть описана разными уравнениями! 2 aR C 2 1 ahR Сравните с уравнением логистического роста. Это уравнение также имеет S-образную форму K N (t ) K N 0 rm ( t t0 ) 1 e N0 Траты на обмен – зависимость обмена от массы тела (эта зависимость уже была рассмотрена в одной из предыдущих лекций) Зависимость скорости основного обмена T (кДж/сут) (на рисунке обмен обозначен R) от массы тела W (кг) для млекопитающих и птиц («кривая от мыши до слона») T = 288 W0.76 Источник : Гильманов Г.Г. 1987. Введение в количественную трофологию и экологическую биоэнергетику наземных позвоночных, с. 32, рис. 4. Исходный источник: Benedict F.G. 1938. Vital Energetics: A Study in Comparative Basal Metabolism. Carnegie Institution of Washington, Washington, DC. С точки зрения массы верно следующее равенство: 1 лось весом 500 кг = 25 000 полёвок весом 20 г каждая ? А с точки зрения потребления энергии? Из лекций А.М. Гилярова НЕТ !!! Для 25 тыс. полёвок потребуется примерно в 11 раз больше энергии, чем для одного лося Из лекций А.М. Гилярова Давайте подсчитаем! Каковы траты на обмен одного лося? Воспользуемся уже известным нам уравнением T = 288 W0.76 где T – траты на обмен в кДж/сут и W – масса тела в кг. Тогда один лось массой 500 кг затрачивает на поддержание жизнедеятельности T (лось) = 32404.8 кДж/сут Каковы траты на обмен одной полевки? Одна полевка массой 20 г затрачивает на поддержание жизнедеятельности T (полевка) = 14.729 кДж/сут Соответственно, 25 тыс. полевок затратят на поддержание жизнедеятельности T (25 тыс. полевок) = 368227 кДж/сут Соотношение между затратами энергии 25 тыс. полевок и одного лося той же массы составляет 11.36 (= 368227/32404.8) Почему так получается? Потому что интенсивность обмена (скорость обмена в расчете на единицу массы) у полевки в 11.36 раз выше, чем у лося. Проверьте! Чем крупнее организм, тем больше ему надо энергии. Связь можно описать степенной функцией: Y = a Wb где Y – скорость дыхания, выраженная или в потреблении кислорода за единицу времени, или непосредственно в единицах энергии, W – масса тела, a и b – коэффициенты, более или менее постоянные для определенной группы организмов. В логарифмической форме: lgY = lg(a Wb) = lga + b lgW Из лекций А.М. Гилярова Вопрос: как от скорости потребления кислорода в мл или г кислорода перейти к единицам энергии? Оксикалорийный коэффициент Оксикалорийный коэффициент – это количество энергии, выделяющееся из того количества органического вещества пищи, на окисление которого расходуется 1 г (или 1 мл) кислорода. Оксикалорийный коэффициент выражается в ккал/г O2 или кДж/г O2. На полное окисление 1 г белка тратится 1.748 г О2. Поскольку калорийность 1 г белка (то есть энергия, освобождающаяся при его окислении) составляет 5.65 ккал, оксикалорийный коэффициент для белка равен 5.65/1.748 = 3.23 ккал/г O2 или 13.6 кДж/г O2. Средний оксикалорийный коэффициент (с учетом содержания в организме белков, жиров и углеводов) принимают равным 3.38 ккал/г O2. Эта величина оксикалорийного коэффициента была впервые рассчитана В.С. Ивлевым в 1934 г. (Ivlev 1934) и до сих пор широко используется (Алимов 1989). Для справки: 1 Ккал = 4.2 кДж, 1 кДж = 239 кал См. А.Ф. Алимов. Введение в продукционную гидробиологию. 1989, с. 13. А.Ф. Алимов приводит значение оксикалорийного коэффициента 14.2 кДж/г O2, что эквивалентно 3.38 ккал/г O2 (3.38 * 4.2 = 14.2). Для гомойтермных (эндотермных) животных при средней температуре тела 39оС: Th = 4.1 0.751 W Для пойкилотермных (эктотермных) животных при температуре 20оС: Tp = 0.14 0.751 W Для одноклеточных при температуре 20оС: Tu = 0.018 0.751 W Из лекций А.М. Гилярова Обратите внимание, как возрастает уровень обмена (обмен особей единичной массы) в ряду одноклеточные – пойкилотермы – гомойотермы Из лекций А.М. Гилярова Max Kleiber (1893–1976) Credit: University of California, Davis Из лекций А.М. Гилярова http://books.nap.edu/openbook.php?record_id=11634&page=52 Обратите внимание, что от общей зависимости отклоняется, причем именно в меньшую сторону, сурок. Как Вы думаете, почему? Из лекций А.М. Гилярова Уточнения: 1) Приведенные оценки метаболизма относятся к «базальному обмену», для организма, находящегося в состоянии покоя. Если организм активен, то полученная величина характеризует активный, или так называемый «полевой» обмен. Эта величина выше базального обмена, но не более чем в несколько раз (Hammond Diamond 1997). У велосипедистов, участвующих в многодневной гонке Tour de France, полевой обмен превышает базальный в 4.2-5.6 раз. Максимальное превышение (6.5 раз), отмечено для выкармливающей потомство самки домовой мыши. Из лекций А.М. Гилярова Уточнения: 2) Показатель степени b = 0.75, описывающий характер зависимости скорости метаболизма от массы тела, не следует рассматривать как строгую константу, аналогичную константам, известным из физики. b – это просто средняя величина, мода статистического распределения множества эмпирических оценок, которые могут варьировать от 0.67 до 0.86 (Darveau et al. 2002). Вот как можно проиллюстрировать тот факт, что 0.75 – это мода статистического распределения (1) Реальное распределение значений показателя степени вокруг 0.75 (по данным разных авторов) (2) Гипотетическое равномерное (без выраженного максимума) распределение значений вокруг 0.75 – дисперсия (т.е. разброс вокруг 0.75) в этом случае больше, чем в случае (1), но среднее сохраняется (3) Гипотетическое распределение значений показателя степени вокруг числа отличного от 0.75 – среднее смещается Случаи (2) и (3) на самом деле не наблюдаются! Из лекций А.М. Гилярова Правило энергетической эквивалентности энергетические траты организма ~ (масса тела)+0.75 T~ Из лекций А.М. Гилярова +0.75 W Зависимость плотности природных популяций разных видов наземных травоядных млекопитающих от массы тела взрослых особей Из лекций А.М. Гилярова Правило энергетической эквивалентности плотность популяции ~ -0.75 (масса тела) N~ -0.75 W Данная зависимость получена только для больших выборок млекопитающих и (отдельно) птиц Из лекций А.М. Гилярова Правило энергетической эквивалентности поток энергии через популяцию как функция массы тела: T N ~ +0.75 W Из лекций А.М. Гилярова, с изменениями -0.75 W Правило энергетической эквивалентности -0.75 W Из лекций А.М. Гилярова +0.75 W = 0 W =1 Что такое продукция Продукция - это совокупность приростов всех особей в популяции, включая в совокупный прирост как прирост уже имеющихся особей, выраженный в энергетических единицах (соматическая продукция), так и энергию, вложенную в образование новых особей (генеративная продукция). Продукцию находят за определенный отрезок времени. Различают продукцию первичную (продукцию растений) и продукцию вторичную (продукцию животных). Новое органическое вещество создается только при образовании первичной продукции в ходе фотосинтеза (и хемосинтеза микроорганизмов). Вторичная продукция представляет собой преобразование органического вещества, потребленного с пищей, в вещество тела организмов-потребителей. Первичную продукцию подразделяют на валовую и чистую (см. следующий слайд) Первичная продукция Классический метод определения первичной продукции фитопланктона – метод темных и светлых склянок (метод Пюттера-Винберга) В водоем на определенную глубину погружают «темные» (например, обернутые светонепроницаемой фольгой) и светлые склянки. Определяют содержание кислорода в склянках в начале периода экспозиции (перед погружением) и в конце. По разнице между изменением содержания кислорода в светлой и темной склянках определяют величину первичной продукции. Обозначения: О – содержание кислорода в воде, Ф – выделение кислорода в ходе фотосинтеза, Д – поглощение кислорода в ходе дыхания растений В светлой склянке изменение содержания кислорода (ΔОС) связано с процессами фотосинтеза и дыхания: ΔОС= Ф – Д В темной склянке изменение содержания кислорода (ΔОТ) связано только с процессом дыхания: ΔОТ = – Д (сравните с первым уравнением, теперь Ф = 0) Вычитая из первого уравнения второе, находим количество кислорода, выделившего в ходе фотосинтеза : ΔОС – ΔОТ = Ф – Д – (–Д) = Ф Зная количество выделившегося кислорода, по стандартному уравнению фотосинтеза находят количество синтезированных углеводов (в форме глюкозы): 6CO2 + 6H2O = C6H12O6 + 6O2. Эта величина первичной продукции называется валовой. Чистая первичная соответствует изменению содержания кислорода в светлой склянке. Вторичная продукция – как совокупность приростов всех особей в популяции P I BtI B0I + P II BeII B0II IV P IV BeIV Bstart + Pg B III start B IV start + III P Bt B0 Be P Ш BtШ Bstart Источник: Полищук Л.В. Динамические характеристики популяций планктонных животных. 1986. Основное уравнение динамики биомассы популяции Bt B0 P Be Сравните с основным уравнением динамики численности популяции Nt N0 [ Births ] [ Deaths ] S-образный рост особи – на примере роста динозавров! На двух верхних графиках штриховыми линиями примерно обозначены точки, соответствующие максимальной скорости роста G Обратите внимание, что уравнения, приведенные на графиках, представляют собой логистическую функцию. Эта же функция используется при описании роста численности популяции (логистический рост) (и она же фигурирует в логистической регрессии)! Источник: Erickson et al. Dinosaurian growth patterns and rapid avian growth rates. Nature 2001 V. 412. P. 429-433 Модель взаимодействия хищник-жертва Вольтерры-Лотки Альфред Джеймс Лотка (A.J. Lotka) Вито Вольтерра (V. Volterra) Из лекций А.М. Гилярова Уравнение для жертвы (1) V – численность (плотность популяции) жертв (victims) P – численность (плотность популяции) хищников (predators) В самом общем виде уравнение для скорости роста жертвы в зависимости от численности хищников и жертв можно записать в следующем виде dV f (V , P ) dt Общее допущение модели (относящееся не только к уравнению для жертвы, но и к уравнению для хищника) Хотя формулировка «в самом общем виде» является общепринятой при написании таких уравнений, на самом деле это уравнение является наиболее общим только с точки зрения учета роли хищников и жертв в динамике численности жертв. Фактически же оно накладывает весьма жесткие ограничения на характер нашего описания изменения численности жертв, поскольку в этом уравнении в принципе не учитывается возможность непосредственного воздействия факторов внешней среды на жертв. Например, если «жертвой» является дафния (для хищника-планктофага), то понижение температуры может оказать непосредственное воздействие на скорость роста численности дафний за счет увеличения длительности развития яиц и замедления скорости размножения дафний. В модели же предполагается, что воздействие внешних факторов возможно только в результате изменения численности жертв и/или хищников. Уравнение для жертвы (2) Частное допущение (1): Единственным фактором, лимитирующим рост жертв, являются хищники Следствие: В отсутствие хищников популяция жертв растет экспоненциально (Почему?) dV rV dt r – удельная скорость популяционного роста жертв В присутствии хищников смертность жертв пропорциональна количеству хищников и их функциональной реакции (рациону) Частное допущение (2): Функциональная реакция хищника относится к типу I, т.е. описывается линейной моделью (при этом выход рациона на плато не предполагается). Тогда уравнение для жертвы имеет вид В химической кинетике выражение типа aVP описывает скорость химической реакции, пропорциональную произведению концентраций взаимодействующих веществ dV rV aVP dt aV = C – рацион хищника или, что то же самое, его функциональная реакция (по типу I) Уравнение для хищника (1) В самом общем виде уравнение для скорости роста хищника в зависимости от численности хищников и жертв можно записать в следующем виде dP g (V , P ) dt (Сравните с уравнением для жертвы. Теперь имеется в виду другая функция – не f, а g) Частное допущение (1): Наш хищник – узкий специалист. (Замечание: хищники бывают специализированные и неспециализированные*.) Он питается только данным видом жертвы. Поэтому в отсутствие жертв его численность падает, причем экспоненциально (как Вы думаете, почему экспоненциально?) dP dP dt d – удельная смертность хищника О специализированных и неспециализированных хищниках прочтите в: Бигон М., Харпер Дж., Таунсенд К. 1989. Экология: Особи, популяции и сообщества, том 2, с. 254-263. Уравнение для хищника (2) Частное допущение (2): В присутствии жертв хищник их, естественно, потребляет и превращает энергию пищи в собственную рождаемость, то есть при потреблении жертв каждая особь хищника производит определенное число новых особей. При этом предполагается, что рождаемость хищника пропорциональна плотности популяции жертв. Зависимость рождаемости хищника от плотности популяции жертв называется численной реакцией (numerical response) хищника на жертву. В модели Вольтерры-Лотки численная реакция хищника описывается линейной моделью. Тогда уравнение для хищника имеет вид dP b1VP dP dt b1 – удельная рождаемость хищника в расчете на одну потребленную жертву, а b1V – численная реакция хищника на жертву. В определенном смысле b1 представляет собой эффективность трансформации энергии пищи в организме хищника (см. ниже). Обратите внимание, что удельная рождаемость b1 не соответствует обычной удельной рождаемости в уравнении динамики численности dN/dt = bN – dN (поэтому она обозначена не b, а b1). Связь между ними такая: b = b1V. Таким образом, в реакции хищника на жертву различают два аспекта – функциональную реакцию, то есть зависимость рациона хищника от концентрации жертв, которая в модели Вольтерры-Лотки описывается линейной функцией (aV), и численную реакцию, то есть зависимость удельной рождаемости хищника от концентрации жертв, которая в модели ВольтеррыЛотки также описывается линейной функцией (b1V). О связи между функциональной и численной реакцией см. следующий слайд. Связь коэффициента численной реакции (b1) и коэффициента функциональной реакции (a) с энергетическим бюджетом организма Pg b1Vw0 b1w0 Pg b1 b1 Pg b1Vw0 ( ) w0 C aV a C a w0 a w0 – масса новорожденной особи Прирост структурной массы Прирост запасных питательных веществ Pg Соматическая продукция, Ps Ps Генеративная продукция, Pg P Продукция, P Ассимилированная (т.е. усвоенная) пища, или ассимилированная энергия, или просто ассимиляция, A T A Траты на обмен, T U C Потребленная пища, C Неассимилированная пища (энергия), U Удельная рождаемость, [время]-1 Уравнение Моно (Monod 1950) b b bmax bmax R kR bmax/2 k Концентрация биогена R константа полунасыщения k Этот график уже был представлен на лекции о ресурсной теории конкуренции Тильмана. Теперь мы понимаем, что на нем изображена численная реакция потребителя – диатомовой водоросли – на концентрацию ресурса – биогена. Этот тип численной реакции по аналогии с соответствующим типом функциональной реакции можно было бы назвать численной реакцией второго типа. Но так, кажется, не говорят. Модель взаимодействия хищник-жертва Вольтерры-Лотки Система уравнений для хищника и жертвы V – численность (плотность популяции) жертв (victims) P – численность (плотность популяции) хищников (predators) dV rV aVP dt dP b1VP dP dt Вспомним, как мы действовали при исследовании модели конкуренции Классическая модель конкуренции: уравнения нулевых изоклин Уравнения конкуренции Вольтерры-Лотки в явном виде решить нельзя, поэтому приходится прибегать к качественному исследованию поведения решений в фазовом пространстве (N1, N2) (это поведение, схематически изображенное в виде стрелочек-векторов, представлено на следующих слайдах) Нулевая изоклина для 1-го вида – Нулевая изоклина для 2-го вида – множество точек в пространстве (N1, N2), для которых скорость роста численности первого вида равна нулю множество точек в пространстве (N1, N2), для которых скорость роста численности второго вида равна нулю dN1 K1 N1 12 N 2 rm1 N1 dt K1 dN1 0 dt dN 2 K 2 N 2 21 N1 rm 2 N 2 dt K2 dN 2 0 dt K1 N1 12 N2 0 K2 N2 21N1 0 1) N1 0, N2 K1 / 12 1) N2 0, N1 K2 / 21 2) N2 0, N1 K1 2) N1 0, N2 K2 Модель взаимодействия хищник-жертва Вольтерры-Лотки Нулевые изоклины Нулевая изоклина для жертвы – Нулевая изоклина для хищника – множество точек в пространстве (V, P), для которых скорость роста численности жертвы равна нулю множество точек в пространстве (V, P), для которых скорость роста численности хищника равна нулю dV rV aVP dt dV 0 dt 0 rV aVP r Pˆ a Нулевая изоклина для жертвы не зависит численности жертв! Нулевая изоклина для жертвы показывает, сколько требуется хищников, чтобы удержать популяцию жертв в равновесии dP b1VP dP dt dP 0 dt 0 b1VP dP d Vˆ b1 Нулевая изоклина для хищника не зависит численности хищников! Нулевая изоклина для хищника показывает, сколько требуется жертв, чтобы удержать популяцию хищников в равновесии Модель взаимодействия хищник-жертва Вольтерры-Лотки Нулевые изоклины: смысл полученных уравнений Нулевая изоклина для жертвы Нулевая изоклина для хищника Чем больше скорость роста Чем больше смертность хищника численности жертвы r, тем больше требуется хищников, чтобы удержать популяцию жертвы в равновесии d, тем больше требуется жертв, r Pˆ a Чем больше рацион хищника (коэффициент функциональной реакции a), тем меньше требуется хищников, чтобы удержать популяцию жертвы в равновесии чтобы удержать популяцию хищника в равновесии d Vˆ b1 Чем больше рождаемость хищника в расчете на одну съеденную жертву (коэффициент численной реакции b1), то есть чем выше эффективность трансформации энергии хищником, тем меньше требуется жертв, чтобы удержать популяцию хищника в равновесии Модель взаимодействия хищник-жертва Вольтерры-Лотки Графики нулевых изоклин, поле направлений и траектория движения системы в фазовом пространстве Нулевая изоклина для жертвы Численность хищников, P Нулевая изоклина для хищника, dP/dt = 0 Нулевая изоклина для жертвы, dV/dt = 0 dV rV aVP dt Нулевая изоклина для хищника dP b1VP dP dt r ˆ P a d ˆ V b1 Численность жертв, V Выводы: (1) Траектория движения системы хищник-жертва представляет собой замкнутую кривую! (Это принимается без доказательства.) (2) Приблизительно траектория движения представляет собой эллипс (3) Движение происходит против часовой стрелки (это мы показали) «Патологически устойчивое равновесие …» Траектории движения системы (Robert May) в системе хищник-жертва Траектория движения системы хищник-жертва и размах колебаний Численность хищников, P хищник-жертва при разных начальных условиях – это набор вложенных замкнутых кривых (приблизительно эллипсов) r Pˆ a d ˆ V b1 Численность Численность жертв, V жертв, V Система, выведенная из положения равновесия, не возвращается к нему и не удаляется от него, а продолжает «кружиться» вокруг этого положения на определенном расстоянии, зависящем от начальных условий. Это расстояние определяет амплитуду колебаний численности хищника и жертвы. С физической (и экологической!) точки зрения такое равновесие неустойчиво в том смысле, что малейшее внешнее воздействие переводит систему на новую траекторию, и к старой траектории система уже не возвращается. Объясните следующее утверждение: “The ellipse indicates that the peak of the predator population occurs when the victim population is at its midpoint, and vice versa” (Gotelli N. J. A Primer of Ecology. 1995: 145-146) Ответ виден из графика! Размах колебаний численности хищника Численность хищников, P r Pˆ a d Vˆ b1 Изменение численности хищников и жертв во времени можно вывести из характера траектории движения системы в фазовом пространстве (см. следующий слайд) Численность Размах колебаний численности жертвы жертв, V Замкнутая траектория в фазовом пространстве соответствует колебаниям численности хищника и жертвы Траектории движения Траектория движения системы (то есть изменение численности) хищник-жертва в фазовом пространстве хищников и жертв во времени (на фазовой плоскости) (временная развертка фазовой траектории) Численность хищников, P I II III IV I P, V III II IV I r ˆ P a d Vˆ b1 Численность жертв, V Зоны I, II, III и IV на левом графике соответствуют зонам с теми же номерами на правом графике хищник жертва Время, t Как видно из графика, колебания численности хищника отстают по фазе от колебаний численности жертвы. Как вы думаете, отстают на сколько? Численность хищников P и жертв V Три свойства взаимодействия хищник-жертва (1) Взаимодействия между хищниками и жертвами порождают колебания. Это общее свойство моделей хищник-жертва, тогда как классические модели конкуренции не дают колебаний (однако более сложные модели конкуренции всетаки порождают колебания! ) (2) Колебания численности хищВремя, t ников отстают по фазе от хищники жертвы колебаний численности жертв. Это (3) Период колебаний равен приблизительно общее свойство, которое для 2 модели Вольтерры-Лотки можно T уточнить: отставание хищников от rd жертв составляет четверть То есть чем быстрее растет жертва в отсутствие периода колебаний – убедитесь хищника (большое r) и чем быстрее падает численность хищника в отсутствие жертвы (большое в этом, глядя на график! d), тем быстрее «крутится» система вокруг положения равновесия. (Несмотря на общность словесной формулировки, приведенная формула - это частное свойство модели Вольтерры-Лотки.) Модель хищник-жертва с внутривидовой конкуренцией для жертвы Пожалуй, наибольшая странность классической модели Вольтерры-Лотки состоит в том, что жертва ограничена только хищником и в отсутствие хищника растет экспоненциально. Что будет, если в уравнение для жертвы включить самолимитирование (то есть внутривидовую конкуренцию)? Предположим, что в отсутствие хищника жертва растет по логистическому уравнению, а хищник воздействует на жертву так же, как в классической модели. (Кстати, эта модель была также изучена Вольтеррой.). Тогда уравнение для жертвы имеет вид dV 2 rV cV aVP dt Модель хищник-жертва с внутривидовой конкуренцией для жертвы Нулевые изоклины Нулевая изоклина для жертвы – Нулевая изоклина для хищника – множество точек в пространстве (V, P), для которых скорость роста численности жертвы равна нулю множество точек в пространстве (V, P), для которых скорость роста численности хищника равна нулю dV rV cV 2 aVP dt dV 0 dt 0 rV cV aVP r c Pˆ V a a 2 Нулевая изоклина для жертвы – это линейная убывающая функция численности (плотности) жертв. dP b1VP dP dt dP 0 dt 0 b1VP dP d Vˆ b1 Нулевая изоклина для хищника не зависит численности хищников. Нулевая изоклина для хищника показывает, сколько требуется жертв, чтобы удержать популяцию хищников в равновесии Модель хищник-жертва с внутривидовой конкуренцией для жертвы Графики нулевых изоклин, поле направлений и траектория движения системы в фазовом пространстве Численность хищников, P Нулевая изоклина для жертвы dV rV cV 2 aVP dt r a Нулевая изоклина для хищника, dP/dt = 0 Нулевая изоклина для жертвы, dV/dt = 0 Нулевая изоклина для хищника dP b1VP dP dt Обратите внимание, что в отсутствие хищника равновесная плотность жертвы (r/c) выше, чем в его присутствии (d/b1) Численность d ˆ V b1 r c жертв, V Траектория движения системы хищник-жертва – спираль, наматывающаяся на точку равновесия (принимается без доказательства). То есть положение равновесия устойчиво! Самолимитирование стабилизирует систему! Классический пример взаимодействия хищник-жертва: рысь и заяц-беляк в Канаде («едят ли зайцы рысей?») Из лекций А.М. Гилярова http://endangeredmammals.files.wordpress.com/2008/01/lynx2.jpg Из лекций А.М. Гилярова BioScience 2001 51(1): 25-35 Из лекций А.М. Гилярова