Тема 4 (часть 1)

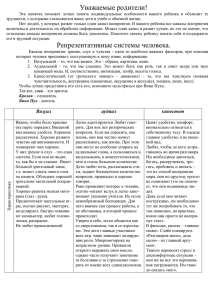
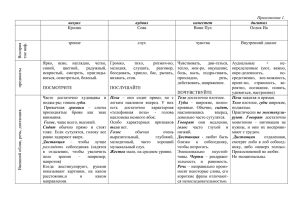
ТЕМА 4 (часть 1)
ЯЗЫК КЛАССИЧЕСКОЙ ЛОГИКИ ПРЕДИКАТОВ ПЕРВОГО ПОРЯДКА
1.
2.
3.
4.
5.
Алфавит ЯКЛП1
Правильно построенные выражения ЯЛП.
*Прикладной язык логики предикатов
Основные синтаксические понятия ЯКЛП1
Выявление логической формы выражений естественного языка с помощью языка
классической логики предикатов.
Литература:
 Бочаров В.А., Маркин В.И. Введение в логику. Гл.5 §1;
 Ивлев Ю.В. Логика. Гл.4, с. 54-59;
 Кузина Е.Б. Логика в кратком изложении и упражнениях. С. 22-28;
 Непейвода Н.Н. Прикладная логика. Часть 1 гл. 3-4.
Определения, которые надо выучить:
Кванторная теория
Элементарная (атомарная) формула
Предметные (индивидные) константы
Сложная (молекулярная) формула
Предметно-функциональные константы
Область действия квантора
Предикаторные константы
Связанное вхождение переменной в формулу
Предметные (индивидные) переменные
Свободное вхождение переменной в формулу
Пропозициональные связки
Связанная переменная
Кванторы
Свободная переменная
Алфавит ЯКЛП1
Местность терма
Выражение языка
Замкнутый терм
Терм ЯКЛП1
Местность формулы
Простые и сложные термы
Замкнутая формула
Формула ЯКЛП1
Задание:
Изучить §1 гл.5 учебника, выписать в тетрадь недостающие определения терминов и
пояснения.
Упражнения1:
1.
Определите, являются ли следующие последовательности символов осмысленными
(правильно построенными) выражениями ЯЛП1 (то есть термами или формулами).
Там, где не указана местность функтора или предиката, считайте, что она та,
которая и требуется записью (Например, в Р(х) Р – одноместный предикат, а в Р(а,у)
– двухместный).
а)
xy
о) ∀хf1(x)
б)
(x,y)
п) ∀aP(a)
в)
P2(x&y)
р) P(a)
г)
¬а
с) y1(x)
д)
h3(g1(f2(a,b)))
т) Q2
е)
a
у) Q1(∀х)
ж)
f2(x,x)
ф) ¬R(x,y)
з)
x1824
2 2
и)
f (h (a,b))
х) ∃xP(a)
к)
h1(f2(a, h1(z)))
ц) ¬∀x¬∀yR(x,y)
л)
f1(P1(a))
ч) ∃y(Q1⊃Р1)
м)
f1(a)& f1(c)
ш) P1(Q1(a))
н)
∃P(x) P(x,х)
щ) ∃x∀y⊃∀х¬∃y
ы) ∃x∀yR(x,y)⊃¬∃y∀x¬R(x,y)
Часть примеров в задании взята из учебников логики Невдобенко О.И., Непейводы Н.Н., Петрова В.Б., а коечто – взято у Льюиса Кэрролла
1
2.
Укажите логические и нелогические константы, входящие в состав данных формул.
а) P (x,c)
б) ∀xP(x,c)
в) ¬∀x∃y((R(x) &R(y))⊃Q(x,y))
г) ∃x(∀yQ(b,c,y)⊃R(x,y))∨(∀z (Q(z)⊃R(z,b)))
Укажите область действия каждого квантора в следующих формулах.
3.
а) ∀xP(x,c)⊃R(x)
б) ∀x(P(x,c)⊃R(x))
в) ∃x(∀yQ(y)⊃R(x,y))∨(∀zQ(z)∨R(z,x))
г) ∀x(P(x,y1)≡∃yQ(y,x)) &∀z(R(x,y)≡R1(y,z))
4.
Определите, какие вхождения переменных являются свободными, а какие связанными
в следующих формулах:
а) ∀xP(x,c)
б) ∀x(P(x)⊃Q(y))
в) ∀x(P(x,y)≡Q(y,x)) &∀z(R(x,y)≡R1(y,x))
г) ∃x(P(x)≡Q(y))
д) ∀x∃y(P(x,y)≡Q(y,x)) &∀x∀y(R(x,y)≡R1(y,x))
5. Определите, какие переменные являются свободными, и какие связанными в следующих
формулах:
а) ∀x(P(x,y)⊃∃yQ(y,z,x))
б) ∃x(∀yQ(y)⊃R(x,y))∨(∀zQ(z)∨R(z,x))
6.
Какие
формулами)?
а) P1(x)
б) P1(a)
из
следующих
формул
являются
предложениями
ЯКЛП
(замкнутыми
в) ∃xP1(x)
г) Q2(c,y)
д) Q3(a2,a2,c)
е) ∃x(P1(x) &Q2(c,y))
ж) ∃y(P1(y) &Q2(c,y))⊃( ∃yR1(y) &Q2(c,y))
з) ∀x∀x4∀y((R(x4) &R(x) &R(y))⊃¬Q3(x,y,x4))
и) ∀x∀x4∀y(R(x4) &R(x) &R(y))⊃¬Q3(x,y,x4)
к) ∃z∀x(R2(x,z)≡Q2(x,x))⊃¬Q3(x,z,z)
7.
Сопоставьте следующим предложениям их логическую структуру в языке КЛП1 с
учетом следующей символизации:
I.
а)
б)
в)
г)
судья – P1
юрист – Q1
восхищаться – R2
жулик – S1
судья Джонс – a
Все судьи – юристы.
Некоторые юристы восхищаются только судьями.
Не все юристы – судьи.
Судья Джонс не восхищается ни одним жуликом.
д) Существуют как юристы, так и жулики, которые восхищаются судьей Джонсом.
е) Все судьи восхищаются только судьями.
ж) Только судьи восхищаются судьями.
II.
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
8.
итальянец – Р1
француз – Q1
любить – R2
Матерацци – а
Зидан – b
футбол – с1
теннис – с2
Матерацци – итальянец.
Матерацци – не француз, а итальянец, а Зидан француз.
И Матерацци, и Зидан любят и футбол, и теннис.
Матерацци любит Зидана, но не взаимно.
Все итальянцы любят футбол.
Ни один итальянец не любит теннис.
Некоторые итальянцы любят теннис.
Лишь некоторые итальянцы любят теннис.
По меньшей мере некоторые французы любят футбол, и Зидан среди них.
Некоторые французы не любят некоторых итальянцев, и некоторые итальянцы не любят
некоторых французов.
Некоторые итальянцы и французы не любят друг друга.
Каждый итальянец не любит хотя бы одного француза.
Выполните упр.1 после §1 пятой главы учебника (с. 169).
9.
Выявите и запишите логические формы следующих высказываний с использованием
языка логики предикатов первого порядка.
а)
Маша – студентка.
б)
Маша и Оля – студентки.
в)
Маша и Оля – ровесницы.
г)
Маша и Оля студентки, и Оля старше Маши.
д)
Москва древнее Нью-Йорка.
е)
Население Москвы больше, чем население Киева.
ж)
Я знаю тебя лучше, чем его.
з)
Я знаю себя лучше, чем тебя.
и)
А.С. Пушкин и Л. Кэролл – не современники.
к)
Некоторые люди страдают бессонницей.
л)
Ни один пингвин не способен освоить логику, и я такой же.
м)
Лишь некоторые англичане разговорчивы.
н)
По меньшей мере некоторые итальянцы пьют эспрессо.
о)
Я тебя не люблю.
п)
Не тебя я люблю.
р)
Не я тебя люблю.
с)
Я люблю тех, кто любит меня.
т)
Я люблю только тех, кто любит меня.
у)
Все водные животные, кроме китов и дельфинов, холоднокровны.
ф)
Все шутки для того и предназначены, чтобы смешить людей.
х)
Ничто разумное не ставит меня в тупик, а логика зачастую ставит.
ц)
Когда кто-то поёт больше часа, он надоедает.
ч)
Все ораторы либо честолюбивы, либо скучны.
ш)
Невесты не бывают лысыми беззубыми занудами, хотя некоторые невесты зануды, у
некоторых есть пломбы, а некоторые носят парики.2
Разумеется, предикат иметь пломбы нельзя рассматривать как отрицание предиката беззубый, так же как
носить парик не является отрицанием предиката быть лысым (к вопросу о символизации)
2
щ)
Каждый знает кого-нибудь.
ы)
Нет человека, который знает всех.
э)
Никто не является современником всем, но каждый кому-нибудь современник.
ю)
Некоторые юристы знают некоторых философов лучше, чем какого бы ни было математика.
я)
Вассал моего вассала не мой вассал.
аа)
Все племена кочевников воевали друг с другом.
бб)
Не всё, что рассказывал барон К.Ф.И. фон Мюнхгаузен, ложь.
вв)
Всякому в Москве не перекланяешься.
гг)
Никто меня не понимает, даже я сам. 3
дд)
Никто, кроме тебя, меня не понимает, не считая меня самого, разумеется.
ее)
В нашей палате все уважают друг друга, не считая А.Македонского, который уважает только
себя.
жж) Волга – самая длинная река в Европе.
зз)
Волга длиннее любой европейской реки.4
ии)
Если x положительно, то x² положительно.
кк)
Если кто-то никогда не выходит из своего дома, то кто-то когда-то приходит к нему домой.
лл)
Джентльмен не может быть похож на лакея, а лакей не может выглядеть джентльменом.
мм)
Некоторые мужчины отращивают бороду, а некоторые ещё и носят тёмные очки.
нн)
Каждый ребёнок мечтает стать взрослым, каждый взрослый мечтает ненадолго вернуться в
детство.
оо)
Чтобы прийти на свадьбу, необходимо приглашение жениха или невесты.
пп)
Для оптимиста все неприятности неожиданны, для пессимиста все неожиданности неприятны.
рр)
Каждый владелец домашних животных относится к ним, как к разумным существам.
сс)
Каждый студент к экзаменационной сессии что-нибудь знает по каждому предмету.
тт)
Не все школьники верят тому, что говорят им учителя, но каждый школьник верит тому, что
написано в школьных учебниках.
уу)
Некоторые категории граждан пользуются правом бесплатного проезда на общественном
транспорте.
Кстати, справедливо для многих студентов, пытающихся что-то произносить на зачете по логике (вообще-то,
не только по логике, и не только на зачетах, да и не только для студентов…)
4
Кстати, почему это высказывание ложно?
3