не изоморфен подмодели сгустка

РАЗРЕШИМОСТЬ ЛИНЕЙНОЙ ЛОГИКИ ЗНАНИЯ
И ВРЕМЕНИ LTK.
Лукьянчук А.Н., Римацкий В.В.
В настоящее время быстро развивается изучение модальных и многомодальных логик, описывающих человеческие рассуждения. Одной из таких
логик является много-модальная логика знания и времени LTK (Linear Time
and Knowledge), которая совмещает в себе модальности по времени и
знанию.
Логика определяется семантически как множество формул, истинных
на LTK-фреймах, где LTK-фрейм это много-модальный фрейм Крипке,
сочетающий в себе линейное и дискретное представление потока времени и
S5-модальность,
определенную
в
каждый
момент
времени
и
представляющую знание.
Язык ℒ 𝐿𝑇𝐾 состоит из счетного множества пропозициональных
переменных 𝑃 ≔ {𝑝1 , … , 𝑝𝑛 , … }, стандартных булевых операций и множества
модальных операторов { □ 𝑇 , □~ , □𝑖 (𝑖 ∈ 𝐼)}. Значение модальных операторов:
(а) □ 𝑇 𝐴 означает, что формула 𝐴 всегда будет истинна, (в) □~ 𝐴 означает, что
𝐴 известна всем в рассматриваемый момент времени, (с) □𝑖 𝐴 (𝑖 ∈ 𝐼)
означает, что действующему агенту “𝑖” известна формула 𝐴 на протяжении
всего потока времени. Мы рассматриваем случай логики LTK, где
количество агентов “𝑖” может быть любым.
LTK-фрейм это много-модальный фрейм ℱ ≔ ⟨𝑊ℱ , 𝑅𝑇 , 𝑅~ , 𝑅1 , … , 𝑅𝑘 ⟩,
где:
(а) 𝑊ℱ это не пустое множество миров,
(в) бинарное отношение 𝑅𝑇 линейно, иртранзитивно,
рефлексивно/иррефлексивно,
(с) бинарное отношение 𝑅~ это универсальное S5-отношение внутри
сгустка по времени,
(d) ∀𝑖, 𝑅𝑖 − некоторое отношение эквивалентности внутри сгустка по
времени.
Доказано следующее утверждение:
Утверждение: В логике LTK справедливо □ 𝑇 □~ 𝛼 ≡ □~ □ 𝑇 𝛼.
Первый важный результат, который мы получили, это финитная
аппроксимируемость логики LTK. Логика 𝐿 называется финитно
аппроксимируемой, если для любой формулы 𝛼 , не доказуемой в 𝐿 ,
существует конечный фрейм (или конечная алгебра), адекватный 𝐿 , на
котором опровергается формула 𝛼 . Из финитной аппроксимируемости
логики следует ее разрешимость. Напомним, что логика 𝐿 является
разрешимой, если существует алгоритм, позволяющий распознать,
принадлежит ли произвольная формула 𝛼 логике или нет.
Далее будем рассматривать логику LTK с интранзитивным и
рефлексивным отношением времени T. Обозначим ее 𝐿𝑇𝐾𝑟
Возьмем формулу 𝐴 такую, что 𝑡𝑑(𝐴) = 𝑛 и 𝐴 ∉ 𝐿𝑇𝐾𝑟 . Тогда
существует 𝐿𝑇𝐾𝑟 − фрейм ℱ ≔ ⟨𝑊ℱ , 𝑅𝑇 , 𝑅~ , 𝑅1 , … , 𝑅𝑘 ⟩ , означивание 𝑉 и
элемент 𝑥 ∈ 𝑊ℱ такие, что ⟨ℱ, 𝑥⟩ ⊭ 𝐴.
Определим модель 𝑁(𝐶(𝑥), 𝑛) следующим образом:
𝑁(𝐶(𝑥), 𝑛) = ⟨𝑊𝑁(𝐶(𝑥),𝑛) , 𝑅𝑇 , 𝑅~ , 𝑅1 , … , 𝑅𝑘 , 𝑉 ′ ⟩,
′
где 𝑊𝑁(𝐶(𝑥),𝑛) = {⋃0≤𝑗≤𝑛 𝐶𝑗′ : 𝐶𝑗 ∈ ℱ; ∀𝑗 𝐶𝑗−1
𝑅𝑇 𝐶𝑗′ ; 𝐶𝑗′ ≅ 𝐶𝑗 как модели} .
Причем мощность модели 𝑁(𝐶(𝑥), 𝑛) ограниченна размером формулы 𝐴 и ее
временной степенью 𝑡𝑑(𝐴).
Доказано, что формула 𝐴 опровергается на конечной модели
𝑁(𝐶(𝑥), 𝑛). То есть справедлива теорема:
Теорема: Логика 𝐿𝑇𝐾𝑟 финитно аппроксимируема.
Использую данный результат, получили следующую лемму:
Лемма 1: Логика 𝐿𝑇𝐾𝑟 разрешима.
Для логики LTK с интранзитивным и иррефлексивным отношением
времени T получены аналогичные результаты.
Так же была построена 𝑛 −характеристическая модель 𝐶ℎ𝐿𝑇𝐾 (𝑛)
логики LTK. Модель Крипке 𝑀 = ⟨ℱ, 𝑉⟩ является 𝑛 −характеристической
для логики 𝐿 тогда и только тогда, когда: (а) 𝐷𝑜𝑚(𝑉) ≔ {𝑝1 , … , 𝑝𝑛 }; (в) для
любой формулы 𝛼 от переменных 𝑝1 , … , 𝑝𝑛 , 𝛼 ∈ 𝐿 ⟺ ℱ ⊨𝑉 𝛼.
Шаг 1. Возьмем класс 𝐹 конечных LTK- фреймов такой, что для
любого фрейма ℱ ∈ 𝐹, ∀𝑤∀𝑧 ∈ 𝑊ℱ (𝑤𝑅𝑇 𝑧 & 𝑤𝑅~ 𝑧). Обозначим 𝒞(𝐹)𝑛 как
класс всех возможных различных не изоморфных моделей 𝐶 = ⟨ℱ, 𝑉⟩, где:
(а) ℱ ∈ 𝐹;
(в) 𝐷𝑜𝑚(𝑉) ≔ {𝑝1 , … , 𝑝𝑛 };
(с) ∀𝑤∀𝑧 ∈ 𝑊ℱ (((𝑉𝑎𝑙𝑉 (𝑤) = 𝑉𝑎𝑙𝑉 (𝑧)) & ({𝑉𝑎𝑙𝑉 (𝑤 ′ )|𝑤𝑅𝑖 𝑤 ′ , ∀𝑖 ∈ 𝐼} =
{𝑉𝑎𝑙𝑉 (𝑤 ′ )|𝑤𝑅𝑖 𝑤 ′ , ∀𝑖 ∈ 𝐼})) ⟹ (𝑤 = 𝑧)).
Пусть 𝑆1 (𝐶ℎ𝐿𝑇𝐾 (𝑛)) ≔ ∐𝒞(𝐹)𝑛 𝐶𝑛 . Первый слой 𝐶ℎ𝐿𝑇𝐾 (𝑛) состоит из
множества 𝑅𝑇 −сгустков со всевозможными означиваниями переменных
𝑝1 , … , 𝑝𝑛 , которые не изоморфны как модели.
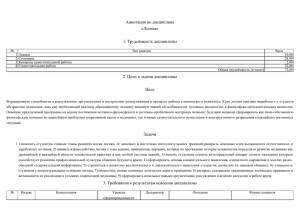
Шаг 2. К каждому 𝑅𝑇 −сгустку 𝐶 из 𝑆1 (𝐶ℎ𝐿𝑇𝐾 (𝑛)) приписываем снизу
все 𝐶𝑗 из 𝒞(𝐹)𝑛 в том случаи, если 𝐶𝑗 не изоморфен подмодели сгустка 𝐶.
Результатом такого добавления станет модель 𝑆2 (𝐶ℎ𝐿𝑇𝐾 (𝑛)).
Шаг 3. Предположим, что модель 𝑆𝑖 (𝐶ℎ𝐿𝑇𝐾 (𝑛)) для 𝑖 ≥ 2 построена
так, что ее фрейм, это LTK-фрейм, и для любых двух сгустков 𝐶𝑗 , 𝐶𝑘 этого
фрейма, если 𝐶𝑗 это непосредственный 𝑅𝑇 −предшественник 𝐶𝑘 , то 𝐶𝑗 не
изоморфен 𝐶𝑘 как подмодель. Модель 𝑆𝑖+1 (𝐶ℎ𝐿𝑇𝐾 (𝑛)) строим следующим
образом. К каждому 𝑅𝑇 −сгустку 𝐶 глубины 𝑖 приписываем снизу все 𝐶𝑗 из
𝒞(𝐹)𝑛 в том случаи, если 𝐶𝑗 не изоморфен подмодели сгустка 𝐶.
В конечном счете, получили модель
𝐶ℎ𝐿𝑇𝐾 (𝑛) ≔ ⟨𝑊ℱ , 𝑅𝑇 , 𝑅~ , 𝑅1 , … , 𝑅𝑘 , 𝑉⟩ ≔ ⋃𝑖∈𝑁 𝑆𝑖 (𝐶ℎ𝐿𝑇𝐾 (𝑛)).
Свойства построенной модели сформулированы в следующих
утверждениях:
Лемма 2: Модель 𝐶ℎ𝐿𝑇𝐾 (𝑛) является 𝑛 −характеристической для
логики LTK.
Лемма 3: Модель 𝐶ℎ𝐿𝑇𝐾 (𝑛) является формульной.
Напомним, что модель 𝑀 = ⟨ℱ, 𝑉⟩ является формульной тогда и только
тогда, когда ∀𝑤 ∈ 𝑊ℱ существует формула 𝛽(𝑤) такая, что ∀𝑧 ∈
𝑊ℱ ((ℱ, 𝑧) ⊨ 𝛽(𝑤) ⟺ 𝑤 = 𝑧).