Взаимное расположение точки и плоскости. Если

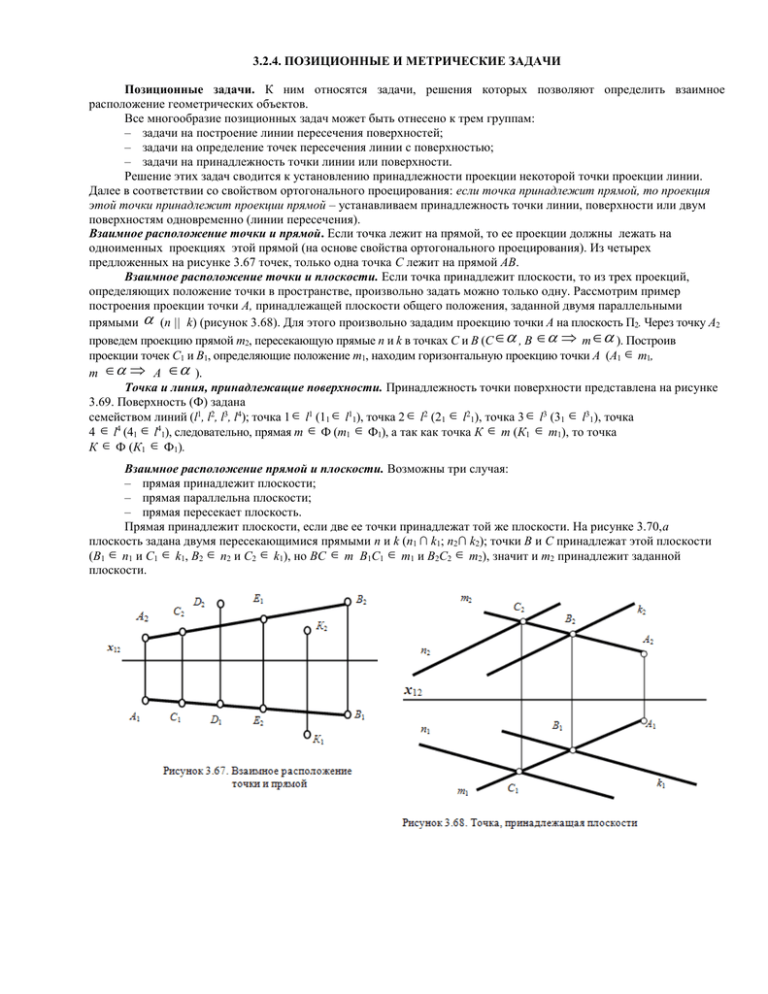
3.2.4. ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ
Позиционные задачи. К ним относятся задачи, решения которых позволяют определить взаимное
расположение геометрических объектов.
Все многообразие позиционных задач может быть отнесено к трем группам:
– задачи на построение линии пересечения поверхностей;
– задачи на определение точек пересечения линии с поверхностью;
– задачи на принадлежность точки линии или поверхности.
Решение этих задач сводится к установлению принадлежности проекции некоторой точки проекции линии.
Далее в соответствии со свойством ортогонального проецирования: если точка принадлежит прямой, то проекция
этой точки принадлежит проекции прямой – устанавливаем принадлежность точки линии, поверхности или двум
поверхностям одновременно (линии пересечения).
Взаимное расположение точки и прямой. Если точка лежит на прямой, то ее проекции должны лежать на
одноименных проекциях этой прямой (на основе свойства ортогонального проецирования). Из четырех
предложенных на рисунке 3.67 точек, только одна точка С лежит на прямой АВ.
Взаимное расположение точки и плоскости. Если точка принадлежит плоскости, то из трех проекций,
определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример
построения проекции точки А, принадлежащей плоскости общего положения, заданной двумя параллельными
прямыми  (n || k) (рисунок 3.68). Для этого произвольно зададим проекцию точки А на плоскость П2. Через точку А2
проведем проекцию прямой m2, пересекающую прямые n и k в точках С и В (С  , B    m  ). Построив
проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1  m1,
m    А  ).
Точка и линия, принадлежащие поверхности. Принадлежность точки поверхности представлена на рисунке
3.69. Поверхность (Ф) задана
семейством линий (l1, l2, l3, l4); точка 1  l1 (11  l11), точка 2  l2 (21  l21), точка 3  l3 (31  l31), точка
4  l4 (41  l41), следовательно, прямая m  Ф (m1  Ф1), а так как точка К  m (К1  m1), то точка
К  Ф (К1  Ф1).
Взаимное расположение прямой и плоскости. Возможны три случая:
– прямая принадлежит плоскости;
– прямая параллельна плоскости;
– прямая пересекает плоскость.
Прямая принадлежит плоскости, если две ее точки принадлежат той же плоскости. На рисунке 3.70,а
плоскость задана двумя пересекающимися прямыми n и k (n1 ∩ k1; n2∩ k2); точки B и C принадлежат этой плоскости
(B1  n1 и C1  k1, B2  n2 и C2  k1), но BC  m B1C1  m1 и B2C2  m2), значит и m2 принадлежит заданной
плоскости.
Прямая (n) принадлежит плоскости (m | | k), если имеет с плоскостью одну общую точку (C) и параллельна
какой-либо прямой, расположенной в этой плоскости (n | | AB), (рисунок 3.70,б).
Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или
пересекает ее.
Для того чтобы определить взаимное расположение прямой (а) и плоскости (), через прямую (а) необходимо
провести вспомогательную секущую плоскость () и установить относительное положение двух прямых (а и в),
последняя из которых является линией пересечения вспомогательной секущей плоскости () и данной плоскости ()
(рисунки 3.71, 3.72,а,б).
Если обе прямые совпадают, то прямая лежит в заданной плоскости.
Параллельность прямых укажет на параллельность прямой и заданной плоскости.
При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное
положение стереометрии: прямая параллельна плоскости, если она параллельна одной
из прямых, лежащих в этой плоскости (см. рисунок 3.71). Проекция прямой на горизонтальную плоскость проекций
b1 совпадает с проекцией а1 и со следом дополнительной плоскости . Проекция прямой b2 параллельна а2,
следовательно, прямая а параллельна плоскости  (BCD).
Пересечение прямых соответствует случаю, когда прямая пересекает заданную плоскость
(а пересекает  в точке К, см. рисунок 3.72).
Рассмотрим пример нахождения точки пересечения прямой и плоскости на эпюре (рисунок 3.72,б). Дана
плоскость  (ВСD) и прямая а. Необходимо найти точку пересечения прямой с плоскостью и определить видимость
прямой по отношению к плоскости.
1. Через горизонтальную проекцию прямой а1 проводится горизонтальный след вспомогательной
горизонтально проецирующей плоскости , тогда
а  .
2. Горизонтальный след плоскости 1 пересекает проекцию плоскости  (В1С1D1) в точках 11 и 21. Для
нахождения фронтальной проекции точек 12 и 22 проводятся линии связи до пересечения с одноименными сторонами
BCD.
3. Прямые а и 1–2 лежат в одной вспомогательной плоскости  и не параллельны, а на фронтальной проекции
наглядно видна точка их пересечения К2.
4. Фронтальная проекция линии пересечения плоскостей 12–22 пересекает фронтальную проекцию а2 в точке
К2, которая и является фронтальной проекцией точки пересечения прямой а с плоскостью (ВСD), с помощью
линии связи находим горизонтальную проекцию К1.
5. Методом конкурирующих точек определяется видимость прямой а по отношению к плоскости  (ВСD).
Конкурирующими точками являются точки 3 и 4 (они имеют одинаковое значение координаты z). Точка 3 находится
ближе к наблюдателю и дальше от плоскости проекций П2, следовательно, на фронтальной проекции 32 перекрывает
42, а К232 будет невидима.
Взаимное расположение двух прямых. Параллельные прямые. Проекции параллельных прямых на любую
плоскость (не перпендикулярную данным прямым) – параллельны. Это свойство параллельного проецирования
остается справедливым и для ортогональных проекций. В общем случае справедливо и обратное утверждение.
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, если
фронтальные и горизонтальные проекции профильных прямых параллельны, то для оценки их взаимного положения
необходимо построить проекцию на профильной плоскости проекций (рисунок 3.73). В рассмотренном случае
проекции отрезков А1В1C1D1; A2В2C2D2, но А3B3 пересекает С3D3, следовательно, прямые не параллельны.
Пересекающиеся прямые. Если прямые пересекаются, то точки пересечения их одноименных проекций
находятся на одной линии связи (рисунок 3.74). В общем случае справедливо и обратное утверждение. Но иногда по
двум проекциям невозможно судить о взаимном расположении
прямых. Например, если одна из прямых параллельна профильной плоскости проекций (рисунок 3.75). На рисунке
видно, что горизонтальная и фронтальная проекции отрезков АВ и СD пересекаются, причем точка пересечения
проекций лежит на одной линии связи. Профильные проекции этих отрезков не пересекаются, следовательно, не
пересекаются и сами отрезки в пространстве. Такие прямые называются скрещивающимися.
В случае, когда пересекающие прямые расположены в общей для них проецирующей плоскости, например,
перпендикулярной фронтальной плоскости проекций (рисунок 3.76), о взаимном расположении прямых, лежащих в
этой плоскости, можно судить по одной горизонтальной проекции.
Скрещивающиеся прямые – прямые, которые не пересекаются и не параллельны между собой, точка
пересечения их одноименных проекций не лежит на одной линии связи (рисунок 3.77). Фронтальные проекции
прямых пересекаются в одной точке, а в пространстве такой точке соответствуют две точки (А и В, из которых одна
принадлежит прямой а, другая – в). Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки
(А и В) находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого
перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. В данном
случае ближе расположена точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе
прямой а, и фронтальная проекция точки В закрывает проекцию точки А.
Пересечение прямой с поверхностью второго порядка строится в общем случае по алгоритму:
1.Прямая (l) заключается в некоторую вспомогательную плоскость (, рисунок 3.78).
2. Строится линия пересечения (КМ) данной поверхности (конуса) и вспомогательной плоскости ().
3. Определяется искомая точка пересечения (К) заданной линии (l) и полученной линии (КМ), при этом надо
помнить, что точка может быть не единственная.
В качестве вспомогательной плоскости целесообразно использовать такую, при пересечении которой с
заданной поверхностью образуются простейшие линии (прямые или окружности). На рисунке 3.78 в качестве
вспомогательной секущей плоскости выбрана плоскость (), проходящая через вершину конуса (S) и включающая
заданную прямую (l). Если же взять горизонтально проецирующую плоскость, то в сечении получится
соответственно гипербола, что значительно усложняет задачу построения.
Основание конуса лежит в горизонтальной плоскости проекций, в этом случае вспомогательная секущая
плоскость пересекает основание конуса по прямой линии (F1D1 и F2D2). В сечении конуса вспомогательной секущей
плоскостью получится треугольник (FDS). Так как полученный треугольник и прямая (l) лежат в одной плоскости
(), точки их пересечения (К и М) и есть точки пересечения прямой (l) с конусом. Видимость определяется с
помощью конкурирующих точек (см. рисунок 3.72).
Взаимное положение двух плоскостей. Две плоскости в пространстве могут либо быть параллельны, либо
пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся
плоскостей.
Плоскости параллельны, если две пересекающиеся прямые (m, n) одной плоскости соответственно
параллельны двум пересекающимся прямым (АС, СВ) другой плоскости (рисунок 3.79).
Построение линии пересечения поверхнос-тей. Линией пересечения двух поверхностей является множество
точек, общих для данных поверхностей. Для определения положения этих точек часто применяется метод
вспомогательных секущих поверхностей-посредников.
В качестве поверхностей-посредников применяют плоскости, сферы, конусы и др. Положение секущих
поверхностей-посредников выбирается так, чтобы они, пересекаясь с заданными поверхностями, давали простые для
построения линии (прямые и окружности). Как вспомогательные секущие поверхности при пересечении прямого
кругового цилиндра, конуса, сферы применяют проецирующие плоскости, параллельные одной из плоскостей проекций
– плоскости уровня.
Линии пересечения двух поверхностей имеют характерные (опорные) точки, с которых рекомендуется
начинать построение. К таким точкам относятся: экстремальные точки – верхняя и нижняя точки относительно той
или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей, точки
границы зоны видимости и т. д.
Метод вспомогательных секущих плоскостей. Линией пересечения двух плоскостей является прямая, для
построения которой достаточно определить две ее точки, общие обеим плоскостям, либо одну точку и направление
линии пересечения плоскостей. Рассмотрим общий случай. Пусть в пространстве заданы две плоскости общего
положения  и  (рисунок 3.80), которые пересекают вспомогательные секущие плоскости уровня (плоскости,
параллельные горизонтальной плоскости проекций
 и ). Линии пересечения заданных плоскостей
( и ) с плоскостями вспомогательными ( и ) – прямые линии (а , а , b , b)., которые пересекаются в точках (АВ),
принадлежащих трем плоскостям (,  и ). Таким образом, эти точки (А и В) являются общими для заданных
плоскостей ( и ), прямая (АВ), проведенная через эти точки, и будет линией их пересечения.
На рисунке 3.81 показано построение линии пересечения плоскостей  (m  n) и  (АВС).
По аналогии с предыдущей задачей, для нахождения линии пересечения данных плоскостей проводятся
вспомогательные секущие плоскости  и . Находятся проекции линий пересечения этих плоскостей с
рассматриваемыми плоскостями. Плоскость  пересекает плоскость  по прямой 3–4, а плоскость  – по прямой 7–8.
Точка М (точка пересечения этих прямых) одновременно принадлежит трем плоскостям ,  и , являясь точкой,
принадлежащей линии пересечения плоскостей  и . Плоскость  пересекает плоскости  и  по прямым 1–2 и 5–6
соответственно. Точка их пересечения (К) расположена одновременно в трех плоскостях (, , ) и принадлежит
прямой линии пересечения заданных плоскостей
( и ). Таким образом, найдя две точки, принадлежащие линии пересечения плоскостей  и  (точки К и М),
проводим через них прямую (КМ).
Видимость определяется методом конкурирующих точек (рисунок 3.72).
Построение линии пересечения плоскостей можно несколько упростить, если задать вспомогательные
проецирующие секущие плоскости через прямые, определяющие плоскость.
Пересечение поверхностей второго порядка плоскостью. В зависимости от положения плоскости по
отношению к плоскостям проекций порой бывает сложно определить линию пересечения ее с поверхностью.
Наиболее простым представляется случай, когда плоскость проецирующая. Рассмотрим решение задачи по
определению линии пересечения сферы фронтально проецирующей плоскостью α (рисунок 3.82).
Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости П1 и П3 в виде эллипса, а на
плоскость П2 – в прямую линию, ограниченную очерком сферы. Необходимо для удобства построения обозначить
опорные точки:
 точки 1 и 8: это две вершины эллипса, определяющие положение малой его оси на горизонтальной
плоскости проекции. Их фронтальные проекции определяют пересечение следа плоскости α с очерком сферы, а
горизонтальные проекции являются соответственно высшей и низшей точками
сечения;
 точки 2 и 3: их профильные проекции принадлежат очерку сферы и определяют зону видимости при
построении эллипса на П3;
 точки 4 и 5: это две вершины эллипса, указывающие на положение большой оси эллипса. Положение их
фронтальных проекций определяется перпендикуляром, опущенным из центра сферы к следу плоскости α;
 точки 6 и 7: принадлежат экватору сферы; их горизонтальные проекции лежат на очерке сферы и
определяют зону видимости при построении эллипса на П1.
Линия пересечения плоскости α и сферы на фронтальной плоскости проекций совпадает со следом плоскости
α2, на котором отмечаем точки
12, …, 82. Для нахождения горизонтальных проекций этих точек в общем случае используется метод
вспомогательных секущих плоскостей (β1 и β2 – горизонтальные плоскости уровня). Например, через точки 22 и 32
проведем след плоскости β12; на горизонтальной плоскости проекций линией пересечения плоскости β1 и сферы
будет окружность β11, точки 21 и 31 лежат на этой окружности, их положение определяется по линиям связи (в
данном случае это осевая линия). Таким образом находятся все точки, кроме 11 и 81, которые, ввиду своего
положения на очерке фронтальной проекции сферы, принадлежат горизонтальной осевой линии на плоскости П1.
Построенные точки 11, …, 81 соединяем плавной кривой линией с учетом видимости.
Конические сечения. В зависимости от положения секущей плоскости линиями сечения поверхности
прямого кругового конуса могут быть (рисунок 3.83): эллипс, парабола, гипербола, а в частных случаях: окружность,
прямая, две пересекающиеся прямые и точка.
Если плоскость Ф пересекает все образующие конической поверхности, т. е. если φ > α, то линией сечения
является эллипс. В этом случае секущая плоскость не параллельна ни одной из образующих конической поверхности.
В частном случае (φ = 90) такая плоскость пересекает поверхность конуса по окружности; и сечение
вырождается в точку, если плоскость проходит через вершину конической поверхности.
Если плоскость Ф параллельна одной образующей поверхности конуса, т. е. φ = α, то линией пересечения
является парабола. В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в
прямую.
Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси), т. е.
φ < α, то линией сечения является гипербола. В случае прохождения плоскости через вершину поверхности конуса
линией сечения могут быть сами образующие, т. е. гипербола вырождается в две пересекающие прямые.
Рассмотрим решение позиционной задачи по определению линии пересечения поверхности вращения и
плоскости общего положения, заданной двумя пересекающимися прямыми α (h ∩ f) (рисунок 3.84). Сечение поверхности параболоида вращения Ф плоскостью α (h ∩ f) и проекции этого сечения на
плоскость, перпендикулярную оси i, являются кривыми, имеющими ось симметрии. Для решения задачи проведем
вспомогательную плоскость β, перпендикулярную оси i. Вспомогательная плоскость пересечет заданную
поверхность по параллели p, фронтальная проекция которой p2 совпадает со следом плоскости β2, а горизонтальная
проекция p1 – является окружностью. Линией пересечения вспомогательной плоскости с заданной плоскостью α (h∩f)
является горизонталь h1.
Параллель p и горизонталь h1, находясь в одной плоскости β, пересекаются в точках 1 и 2, которые
принадлежат искомой линии. Полученные точки симметричны друг другу относительно плоскости σ,
перпендикулярной хорде 1–2 и проходящей через ее середину. Заметим, что плоскость σ, являясь множеством точек,
равноудаленных от концов хорды 1–2, пройдет через ось i поверхности вращения, все точки которой также
равноудалены от точек 1 и 2.
Очевидно, что для любой другой пары точек, расположенных на концах хорд других окружностей (но
параллельных хорде 1–2), плоскость σ будет также являться плоскостью симметрии. Следовательно, кривая сечения
поверхности вращения плоскостью α представляет собой кривую, осью симметрии которой служит линия
пересечения плоскостей α и σ – прямая, проходящая через точку s (линия наибольшего ската плоскости α,
проходящая через ось поверхности вращения). Таким образом, используя вспомогательные горизонтальные секущие
плоскости, можно получить необходимое множество точек для построения линии пересечения плоскости α и
поверхности Ф.
Однако если не учитывать характерные точки, определяющие границу зоны видимости линии пересечения,
высшую и низшую точки этой линии, построение будет менее точным.
Точки, определяющие зону видимости (3 и 4), расположены на главном меридиане поверхности. Для их
построения через этот меридиан проведем вспомогательную секущую плоскость γ, параллельную фронтальной
плоскости проекций. Плоскость γ пересекает α по фронтали f1, которая, в свою очередь, находясь в одной плоскости
с главным меридианом, пересекается с ним в искомых
точках 3 и 4.
Высшая и низшая точки сечения (5 и 6) находятся на линии наибольшего наклона (линии ската) плоскости α,
проходящей через ось поверхности Ф, т. е. на прямой s. Эту прямую и меридиан поверхности, плоскость которого
совпадает с прямой s, повернем вокруг оси i до положения s1, когда прямая s и плоскость меридиана окажутся
параллельными П2. Отметим при этом, что точка К пересечения прямой s с осью i остается неподвижной, а
вращаемый меридиан в итоге совместится с главным меридианом – очерком фронтальной проекции поверхности
вращения. Обозначим точки пересечения фронтальной проекции главного меридиана и повернутой прямой как точки
51 и 61.
Возвращая обратным поворотом прямую s с найденными точками в исходное положение, находим положение
точек 5 и 6. Соединив эти точки кривой с учетом видимости, получим линию пересечения плоскости α с
поверхностью Ф.
Пересечение многогранника с поверхностью вращения. Аналогично рассматривается случай пересечения
поверхности вращения несколькими плоскостями. На рисунке 3.85 представлено решение задачи по нахождению
проекций линий пересечения поверхности конуса с тремя гранями призмы.
β2
γ2
12
φ2
m2=52=42
p2
7282
92102
62 α2
73
43
93
63
33 m3
p3 53
83
103
m1
71
41
91
m1
11
13
23
22=32
21
61
p1
31
10
81
51
1
Рисунок 3.85. Пересечение конуса с призмой
Рассмотрим последовательность нахождения проекций точек 4 и 5. Через фронтальные проекции этих точек
проводится вспомогательная секущая плоскость φ. Эта плоскость пересекает конус по параллели p, а грань призмы –
по прямой линии m, параллельной ребру. На горизонтальной плоскости проекций пересечения p1 и m 1 определяют
положение точек 41 и 51. Для более точного построения кривых линий пересечения поверхностей нужно найти еще
несколько точек и можно ввести дополнительные секущие плоскости α, β, γ. Проекции всех точек необходимо
соединить с учетом видимости – в данном случае видимость линий определяется видимостью граней призмы.
Метрические задачи. Метрическими называются задачи, решения которых позволяют определить значения
различных величин: величину угла, расстояния между точками, площадь сечения, построение угла и отрезка с
заданными значениями градусной или линейной величины и др.
При ортогональном проецировании геометрические объекты, произвольно расположенные по отношению к
плоскостям проекций, проецируются на эти плоскости с искажением их метрических характеристик. В основе
алгоритма решения любой метрической задачи лежит свойство ортогонального проецирования: плоская фигура,
параллельная плоскости проекций, проецируется на эту плоскость в натуральную величину.
В задачах на построение проекции прямого угла используется теорема: если хотя бы одна сторона прямого
угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость
проецируется в прямой угол.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой
плоскости. В качестве пересекающихся прямых чаще всего выбирают горизонталь и фронталь плоскости (рисунок
3.86), так как они проецируются в натуральную величину на соответствующие плоскости проекции (hП1, а fП2,
следовательно, h1 и f2 – натуральные величины).
На чертеже: прямая перпендикулярна плоскости, когда горизонтальная проекция этой прямой
перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали
этой плоскости ( а1  h1, а2  f2).
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким
образом, чтобы построить плоскость  (n ∩ m), перпендикулярную заданной плоскости
 (h ∩ f), необходимо сначала построить прямую, перпендикулярную данной плоскости (построение прямой а к
плоскости DBC дано на рисунке 3.86), и через эту прямую провести искомую плоскость
(рисунок 3.87).
При решении метрических задач, связанных с определением истинных размеров, изображенных на эпюре
геометрических объектов, могут встретиться значительные трудности, если заданные проекции не подвергнуть
специальным преобразованиям. Рассмотрим на примере: определения расстояния от точки (А) до прямой (m).
Искомый отрезок должен быть перпендикулярен этой прямой. В этих двух случаях прямая mП2, значит на эту
плоскость угол будет проецироваться без искажения. Но так как в первом случае (рисунок 3.88,а) m  П1, то отрезок
АК  m проецируется на плоскость П1 в натуральную величину. А во втором случае (рисунок 3.88,б) удалось
построить только проекцию искомого
отрезка.
Сопоставление приведенных чертежей показывает, что трудности решения одной и той же задачи существенно
зависят от положения геометрических объектов относительно плоскостей проекций. Переход от общего положения
геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемого
отрезка и системы координат.
При ортогональном проецировании это достигается двумя путями.
1. Перемещение в пространстве проецируемого объекта так, чтобы он занял определенное положение
относительно плоскостей проекций: параллельное или перпендикулярное искомому объекту. Это метод
плоскопараллельного перемещения или вращения.
2. Проецирование геометрического объекта на дополнительную (или дополнительные) плоскость проекций,
которая по отношению к нему занимает частное положение (параллельное или перпендикулярное искомому объекту).
Это метод замены плоскостей проекций.
Метод плоскопараллельного перемещения. Изменить взаимное положение проецируемого объекта и
плоскостей проекций можно, изменив положение геометрического объекта так, чтобы он занял по отношению к
плоскости проекции частное положение (например, перпендикулярное). При этом траектория движения точек
объекта – произвольная линия – находится в параллельных плоскостях, которые в свою очередь параллельны какойлибо плоскости проекций (рисунок 3.89). Проекция плоской фигуры хотя и меняет свое положение, но остается
конгруэнтной своей проекции в исходном положении.
Свойства плоскопараллельного перемещения:
– при всяком перемещении точек в плоскости, параллельной плоскости П1, ее фронтальная проекция
перемещается по прямой, параллельной оси х (рисунок 3.90);
– в случае произвольного перемещения точки в плоскости, параллельной П2, ее горизонтальная проекция
перемещается по прямой, параллельной оси х.
Траектории перемещения точек отрезка АВ параллельны плоскости проекций (П1, рисунок 3.90).
В зависимости от положения плоскостей перемещения по отношению к плоскостям проекций и вида кривой,
определяющей траекторию перемещения точек, можно выделить следующие частные случаи метода
плоскопараллельного перемещения:
– вращение вокруг оси, перпендикулярной плоскости проекций;
– вращение вокруг оси, параллельной одной из плоскостей проекций, но не перпендикулярной другим
плоскостям проекций;
– вращение вокруг оси, принадлежащей
плоскости проекций (вращение вокруг следа плоскости), – способ совмещения.
Метод вращения вокруг оси, перпендикулярной плоскости проекций. Траекторией движения
геометрического объекта является дуга окружности, центр которой находится на оси, перпендикулярной этой же
плоскости проекций. Рассмотрим на примере (рисунок 3.91): для определения натуральной величины отрезка прямой
общего положения АВ выберем ось вращения, перпендикулярную горизонтальной плоскости проекций и
проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций
(горизонтальная проекция отрезка параллельна оси x). При этом точка В не изменит своего положения, а точка А
переместится в другое положение, при котором отрезок станет параллелен фронтальной плоскости проекции.
Соответственно изменятся горизонтальная и фронтальная проекции точки А: В1А'1 параллельна x, а длина полученной
фронтальной проекции В2А'2 определяет действительные размеры
отрезка.
Метод замены плоскостей проекций. Изменение взаимного положения проецируемой фигуры и плоскостей
проекций методом перемены плоскостей проекций достигается путем замены плоскости П2 (П1 или П3) другой
плоскостью – П4 (рисунок 3.92).
Последовательный переход от одной системы плоскостей проекций к другой осуществляется с учетом
следующего правила: расстояние от новой проекции точки до новой оси должно равняться расстоянию от
заменяемой проекции точки до
заменяемой оси.
Рассмотрим на примере: необходимо определить натуральную величину отрезка АВ прямой общего положения
(рисунок 3.92).
Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную
величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельную отрезку АВ и
перпендикулярную плоскости П1. Система плоскостей П1/П2 заменена
системой П1/П4, причем в новой системе плоскостей проекция отрезка А4В4 равна натуральной величине отрезка АВ.
Угол наклона А4В4 к оси ОХ14 (α) равен углу наклона прямой АВ к горизонтальной плоскости проекции. Аналогично
можно найти величину отрезка АВ, если П4 будет  П2. В этом случае на эту плоскость спроецируется в натуральную
величину угол наклона прямой АВ к П2.