Пример 3
реклама

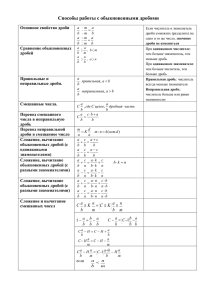
Сложение и вычитание рациональных дробей Сложение и вычитание рациональных дробей c одинаковыми знаменателями При сложении обыкновенных дробей с одинаковыми знаменателями 2 складывают их числители, а знаменатель оставляют прежним. Например, + 3 7 = 2+3 7 7 5 = . 7 Таким же образом складывают 𝑎 𝑏 𝑎+𝑏 знаменателями: + = , с0. 𝑐 𝑐 любые 𝑐 𝑐 Пример 1. Сложить дроби 3𝑎−7𝑏 2𝑎+2𝑏 + 15𝑎𝑏 15𝑎𝑏 𝑎2 +9 5𝑎−15 − 6𝑎 5𝑎−15 𝑥 2 −3 𝑥 2 +2𝑥 + 2 𝑎2 +9 5𝑎−15 𝑎2 +9−6𝑎 = 𝑥 2 +2𝑥 − 15𝑎𝑏 одинаковыми знаменателями выполняется 5𝑎−15 2𝑥−1 𝑥 2 +2𝑥 = . = 15𝑎𝑏 Пример 3. Упростить выражение Решение. 2𝑎+2𝑏 и 3𝑎−7𝑏+2𝑎+2𝑏 = 15𝑎𝑏 𝑐 3𝑎−7𝑏 Пример 2. Вычесть из дроби Решение. с 𝑐 Вычитание дробей с одинаковыми 𝑎 𝑏 𝑎−𝑏 аналогично сложению: − = , с0. Решение. дроби 5𝑎−5𝑏 дробь = 15𝑎𝑏 6𝑎 5(𝑎−3) 𝑥 2 +2𝑥 + 15𝑎𝑏 = 𝑎−𝑏 3𝑎𝑏 . Ответ: 𝑎−𝑏 Ответ: 𝑎−3 . = 𝑎−3 5 2 𝑥 2 +2𝑥 − 2𝑥−1 𝑥 2 +2𝑥 3𝑎 2𝑥−𝑎 5 . 𝑥 2 −3+2−(2𝑥−1) 𝑥 2 −1−2𝑥+1 𝑥 2 −2𝑥 𝑥(𝑥−2) 𝑥−2 = 𝑥 2 +2𝑥 𝑥 2 +2𝑥 = = = 𝑥 2 +2𝑥 𝑥(𝑥+2) 𝑥+2 Ответ: Пример 4. Сложить дроби 3𝑎𝑏 5𝑎−15 (𝑎−3)2 𝑥 2 −3 5(𝑎−𝑏) = и 6𝑥 𝑎−2𝑥 𝑥−2 𝑥+2 . Решение. Знаменатели дробей являются противоположными выражениями. Изменим знаки в знаменателе второй дроби и перед этой 6𝑥 6𝑥 дробью. Получим: =− . Теперь можно применить правило вычитания 𝑎−2𝑥 2𝑥−𝑎 дробей с одинаковыми знаменателями: 3𝑎 2𝑥−𝑎 − 6𝑥 2𝑥−𝑎 = 3𝑎−6𝑥 −3(2𝑥−𝑎) 2𝑥−𝑎 = 2𝑥−𝑎 = −3. Ответ: - 3 Задания для самостоятельной работы 1. Выполните сложение или вычитание дробей: 𝑥 𝑦 3 3 1) + 6) 2𝑐−𝑥 𝑏 𝑎 2𝑎 𝑦 𝑦 2) + − 𝑥 7) 𝑏 𝑚 𝑝 − 𝑥+𝑦 3) 𝑚−𝑝 9 𝑏2 8) 𝑝 2𝑎 𝑥 − 9 3𝑏2 + 𝑎 𝑏 5 5 4) − 9) 2𝑎 2𝑥 3 + 5) 1−𝑥 5𝑏 2 𝑎 10) 3 − 𝑚+𝑞 𝑝 13𝑏2 𝑎 − 𝑚−𝑞 𝑝 2. Выполните действия: 1) 5) 9) 𝑥+5 9 𝑥+2 − 8𝑐+25 6𝑐 2) 9 5−2𝑐 + 17−12𝑥 𝑥 6) 6𝑐 + 10−𝑥 7𝑦−13 10𝑦 2𝑥−3𝑦 10) 𝑥 4𝑥𝑦 − + 12𝑝−1 3𝑝2 2𝑦+3 3) 10𝑦 11𝑦−2𝑥 7) 4𝑥𝑦 − 𝑎+𝑏 𝑎−2𝑏 − 6 5𝑎+𝑏5 8𝑏 4) 6 − 5𝑎−7𝑏5 8𝑏 8) 11𝑥−5 14𝑥 3𝑥−𝑦 4 4𝑦 5 + 3𝑥−2 14𝑥 𝑦 4 +3𝑥 − 4𝑦 5 1−3𝑝 3𝑝2 3. Выполните действия: 1) 4) 𝑎−2 8𝑎 + 7𝑦−5 12𝑦 2𝑎+5 8𝑎 − 3−𝑎 − 2) 8𝑎 10𝑦−19 12𝑦 + 10−15𝑦 5) 12𝑦 7) 11𝑎−2𝑏 4𝑎 5𝑐−2𝑑 4𝑐 + 2𝑎−3𝑏 4𝑎 3𝑑 − 4𝑐 + − 𝑎−𝑏 3) 4𝑎 𝑑−5𝑐 6) 4𝑐 8) 9) 3𝑝−𝑞 5𝑝 2𝑎 𝑏 − 4𝑏−2 3𝑏 − 2𝑝+6𝑞 5𝑝 1−6𝑎 𝑏 − + 2𝑏−1 3𝑏 + 𝑝−4𝑞 5𝑝 13−8𝑎 𝑏 + 1 3𝑏 10) 4. Упростите выражение: 1) 5) 9) 16 𝑥−4 − 𝑥−3 𝑥 2 −64 𝑥2 2) 𝑥−4 11 + 𝑥 2 −64 𝑥 2 +25 10𝑥 (𝑥−5) (5−𝑥)3 + 3 6) 3𝑎−1 3𝑏−1 𝑎2 −𝑏 𝑎2 −𝑏2 − 2 𝑥2 (𝑥−5) 10) − 2 𝑥2 𝑥 2 −16 3) 25 7) (5−𝑥)2 − 2𝑎+𝑏 2𝑏−5𝑎 (𝑎−𝑏) (𝑎−𝑏)2 + 2 64−2𝑎𝑏 (𝑎−8)2 + 2𝑎𝑏−𝑎2 4) 25 𝑎+5 8) (8−𝑎)2 8(𝑥−2) 𝑥 2 −16 5. Найдите значение выражения: 1) 3) 5) 𝑥 2 +1 𝑥−3 − 𝑎2 −43 𝑎−6 9𝑏−1 𝑏2 −9 10 𝑥−3 + − при х=97 7 𝑎−6 при а=10,25 6𝑏−10 𝑏2 −9 при b=3,5 2) 4) 6) 𝑦+7 𝑦 2 −25 𝑎2 −12𝑏 𝑎2 −3𝑎𝑏 2𝑦+2 𝑦 2 −25 − 𝑥 2 −2𝑦 𝑥 2 +𝑥𝑦+2𝑥 7) 8) 9) 10) 6. Упростите выражение: − при у= - 51 3𝑎𝑏−4𝑎 𝑎2 −3𝑎𝑏 − при а= - 0,8; b= - 1,75 4−𝑥𝑦 𝑥 2 +𝑥𝑦+2𝑥 при х=20, у=22,5 − 𝑎2 𝑎+5 1) 5) 9) 5𝑝 + 2𝑞−𝑝 𝑎 𝑎2 −9 + 𝑎 2𝑎−𝑏 + 10𝑞 2) 𝑝−2𝑞 3 6) 9−𝑎2 3𝑎−𝑏 𝑎2 +16 𝑎−4 2𝑚 𝑚−𝑛 10) 𝑏−2𝑎 + 𝑦2 𝑦−1 8𝑎 + 3) 4−𝑎 2𝑛 7) 𝑛−𝑚 10𝑝 𝑝−𝑞 3𝑝 + 4) 𝑞−𝑝 𝑥 2 +9𝑦 2 𝑥−3𝑦 + 6𝑥𝑦 8) 3𝑦−𝑥 𝑥−3 𝑥−1 5𝑎 𝑎−𝑏 2 − 1−𝑥 + 5𝑏 𝑏−𝑎 1 + 1−𝑦 7. Представьте дробь в виде суммы или разности дробей: 1) 6) 𝑥 2 +𝑦 2 2) 𝑥4 𝑦+𝑧 2 7) 𝑧 2𝑥−𝑦 3) 𝑏 𝑎2 −2𝑎+4 8) 𝑎 𝑎2 +1 4) 2𝑎 5𝑛−12 9) 𝑚 𝑎2 −3𝑎𝑏 5) 𝑎3 36−𝑎2 𝑥+2 10) 𝑎2 𝑥 𝑏2 +3𝑏−6 𝑏 Сложение и вычитание рациональных дробей c разными знаменателями Сложение и вычитание дробей с разными знаменателями сводится к сложению и вычитанию дробей с одинаковыми знаменателями. 𝑎 𝑐 Пусть нужно сложить дроби и . Приведем эти дроби к общему 𝑏 𝑑 знаменателю bd. Для этого числитель и знаменатель первой дроби умножим на 𝑎 𝑎𝑑 𝑐 d, а числитель и знаменатель второй дроби умножим на b. Получим: = , = 𝑐𝑏 𝑑𝑏 𝑏 . Теперь можно воспользоваться правилом 𝑎 𝑐 𝑎𝑑 𝑐𝑏 𝑎𝑑+𝑐𝑏 одинаковыми знаменателями: + = + = . 𝑏 𝑎 𝑏 𝑏𝑑 𝑑 𝑑 𝑏𝑑 𝑑𝑏 сложения дробей с 𝑑𝑏 Аналогично поступают при вычитании дробей с разными знаменателями: 𝑎𝑑 𝑐𝑏 𝑎𝑑−𝑐𝑏 − = − = . 𝑐 𝑑 𝑏𝑑 𝑑𝑏 𝑑𝑏 При сложении и вычитании дробей с разными знаменателями часто удается найти более простой общий знаменатель, чем их произведение. Пример 1. Сложить дроби 𝑥 4𝑎3 𝑏 и 5 6𝑎𝑏4 . Решение. Общий знаменатель дробей равен 12𝑎3 𝑏4 . Дополнительные множители равны 3𝑏 3 и 2𝑎2 . 𝑥 4𝑎3 𝑏 + 5 6𝑎𝑏4 = 𝑥∙3𝑏3 +5∙2𝑎2 12𝑎3 𝑏4 = 3𝑥𝑏3 +10𝑎2 12𝑎3 𝑏4 . Ответ: Пример 2. Преобразуйте выражение Решение. = 3𝑏+3𝑎 𝑎𝑏(𝑎+𝑏) = 𝑎+3 𝑎2 +𝑎𝑏 − 3(𝑏+𝑎) 𝑏−3 𝑎𝑏+𝑏2 = = 𝑎+3 𝑎(𝑎+𝑏) − 𝑎+3 𝑎2 +𝑎𝑏 𝑏−3 𝑏(𝑎+𝑏) = − 𝑏−3 𝑎𝑏+𝑏2 3𝑥𝑏3 +10𝑎2 12𝑎3 𝑏4 . (𝑎+3)𝑏−(𝑏−3)𝑎 𝑎𝑏(𝑎+𝑏) = 𝑎𝑏+3𝑏−𝑎𝑏+3𝑎 𝑎𝑏(𝑎+𝑏) = 3 𝑎𝑏(𝑎+𝑏) 𝑎𝑏 Ответ: 3 𝑎𝑏 Пример 3. Упростите выражение 𝑎 − 1 − Решение. 𝑎 − 1 − 𝑎2 −3 𝑎−1 = 𝑎+1 𝑎2 −3 − 1 𝑎+1 = 𝑎2 −3 . 𝑎+1 (𝑎−1)(𝑎+1) − 𝑎+1 𝑎2 −3 𝑎+1 = 𝑎2 −1−𝑎2 +3 𝑎+1 2 = . 𝑎+1 Ответ: 2 𝑎+1 Задания для самостоятельной работы 1. Выполните сложение или вычитание дробей: 𝑥 𝑦 2 3 1) + 6) 17𝑦 24𝑐 𝑎 𝑏2 𝑏 𝑎 𝑞 𝑝 𝑝 𝑞 2) − 25𝑦 − 7) + 36𝑐 3) 8) 5𝑥 8𝑦 𝑎 5𝑐 + + 𝑥 𝑐 𝑑 4 12 4) − 4𝑦 3𝑎 9) 4𝑐 5𝑎 − 18𝑏 5) 7𝑎 3 2𝑥 10) 45𝑏 − 𝑚 2 3𝑥 − 𝑝 𝑞 3𝑝 2. Выполните сложение или вычитание дробей: 1) 6) 5𝑦−3 6𝑦 7𝑥+4 8𝑦 + − 𝑦+2 2) 4𝑦 3𝑥−1 𝑏+2 15𝑏 − 3𝑐−5 3) 45𝑐 7) 6𝑦 3𝑥+5 35𝑥 + 𝑥−3 4) 21𝑥 8) 8𝑏+𝑦 40𝑏 − 6𝑦+𝑏 5) 30𝑦 9) 15𝑎−𝑏 12𝑎 − 𝑎−4𝑏 9𝑎 10) 3. Выполните действия: 1) 5) 9) 𝑥−𝑦 𝑥𝑦 − 3𝑚−𝑛 3𝑛𝑚2 𝑐 2 +𝑥 2 𝑐 2𝑥5 𝑥−𝑧 2) 𝑥𝑧 − − 2𝑛−𝑚 2𝑚𝑛2 𝑐+𝑥 6) 𝑝−𝑞 𝑝+𝑞 𝑝3 𝑞 𝑝2 𝑞 3 2𝑥−7𝑦 2𝑥 2 𝑦 10) 𝑐 3𝑥4 − 2 − 𝑎2 −𝑎+1 𝑎3 𝑥 3) 5𝑦−8𝑥 7) 5𝑥𝑦 2 − 3𝑏+2𝑐 − 9𝑏2 𝑐 2𝑐−5𝑏 3𝑏2 −5𝑏−1 𝑏2𝑦 4) 6𝑏𝑐 2 + 5𝑏−3 8) 𝑏𝑦 𝑎−2𝑏 3𝑏 − 𝑏−2𝑎 3𝑎 1+𝑐 𝑐 3 +𝑦 4 𝑐 3𝑦 𝑐 2𝑦8 − 4 𝑥 2 −1 𝑎𝑥 3 4. Преобразуйте в дробь выражение: 1) 𝑥 + 1 2) 3𝑎 − 𝑦 6) 5𝑏 − 2 7) 2𝑝 − 𝑏 𝑎 3) 4 4𝑝2 +1 2𝑝 𝑎2 +𝑏 𝑎 8) 𝑐 − −𝑎 4) (𝑏+𝑐)2 (𝑎−𝑏)2 +𝑏 2𝑎 9) 5𝑦 2 − 2𝑏 15𝑦 2 −1 3 1 5) − 𝑎 𝑎 10) 𝑎 + 𝑏 − 𝑎−3 3 5. Представьте в виде дроби: 𝑎 1) 1 − − 5 5) 3 − 9) 𝑥 − 𝑏 4 2𝑥−𝑦 4 9 𝑥−3 2) + 𝑥+4𝑦 −3 12 𝑎−2 2 −1− 3 5 𝑥 𝑥 6) − 2 − 10) 𝑎2 − 6. Представьте в виде дроби: 𝑎−3 𝑎4 +1 𝑎2 −1 3 3) 4𝑎 − 7) +1 6𝑎−4𝑏 5 𝑎−1 4 − − 𝑎+2 𝑏+7𝑎 3 3 −2 4) 𝑥 − 𝑥−𝑦 2 + 𝑥+𝑦 1 1 𝑎 𝑏 8) 12 − − 4 1) 6) 𝑏−𝑐 + 𝑏 𝑝 3𝑝−1 𝑏 2) 𝑏+𝑐 𝑝 − 7) 3𝑝+1 𝑚 𝑚−𝑛 𝑎+𝑏 − − 2𝑎 𝑛 3) 𝑚+𝑛 𝑏 𝑎 − 𝑎+2 𝑎 4) 𝑎−2 8) 𝑥+1 𝑥−2 − 𝑥+3 5) 𝑥 9) 2𝑎 2𝑎−1 − 1 2𝑎+1 10) 𝑎+𝑏 7. Выполните действия: 1) 6) 1 2𝑎 4−2𝑎3 + 7 2) 𝑎10 2𝑥𝑦−1 − 4𝑥 3 3𝑦−𝑥 7) 6𝑥 2 2𝑎−3𝑏 𝑎2 𝑏 1−𝑏2 + 3𝑎𝑏 4𝑎−5𝑏 + 3) 𝑎𝑏2 3𝑏3 −1 1−𝑥 + 𝑥3 1 4) 𝑥2 8) 𝑎+𝑏 𝑎−𝑏 + 𝑎2 𝑥−2𝑦 5) 𝑎𝑏 9) 𝑥𝑦 2 − 2𝑦−𝑥 𝑥2𝑦 10) 6𝑎𝑏2 8. Представьте в виде дроби: 1) 1 𝑎𝑏 + 1 𝑎𝑐 + 1 2) 𝑏𝑐 5) 𝑏−𝑎 + 𝑎𝑏 𝑐−𝑏 − 𝑏𝑐 𝑐−𝑎 3) 𝑎𝑐 6) 9) 7) 𝑎𝑏−𝑏 𝑎 𝑎𝑏−𝑎 − 𝑏 3𝑎𝑏+2𝑏2 𝑎𝑏 − 𝑎2 −𝑏2 − 4) 𝑎𝑏 𝑎+2𝑏 + 𝑎 𝑎−2𝑏 8) 𝑏 10) 9. Преобразуйте в дробь выражение: 1) 5) 9) 3𝑥 2𝑦 − 5(𝑥+𝑦) 𝑎2 3(𝑥+𝑦) 𝑏2 − 5(𝑎−𝑏) 𝑏2 −4𝑏𝑦 2𝑎2 −𝑏𝑦 2) 6) 4(𝑎−𝑏) − 4𝑦 3 𝑎𝑥−𝑎𝑦 13𝑐 2 3) 𝑏𝑦−𝑏𝑥 12𝑏 − 𝑏𝑚−𝑏𝑛 10) 𝑏−2𝑦 + 7) 𝑐𝑛−𝑐𝑚 4𝑦 3𝑥 2 +2𝑥𝑦 − 𝑎 2𝑥+4 𝑝 2𝑥+1 − − 𝑎 3𝑥+6 𝑝 3𝑥−2 𝑝 4) 7𝑎−14 𝑎2 8) 𝑎𝑥−𝑥 2 + + 1 2−𝑎 𝑥 𝑥−𝑎 9𝑥 3𝑥𝑦+2𝑥 10. Преобразуйте выражение: 1) 𝑎2 +3𝑎 𝑎𝑏−5𝑏+8𝑎−40 − 𝑎 𝑏+8 4) 2) 𝑦 3𝑥−2 − 3𝑦 6𝑥𝑦+9𝑥−4𝑦−6 5) 7) 3) 6) 8) 𝑥2 3𝑎𝑥−2−𝑥+6𝑎 3𝑥 2𝑦+3 + − 𝑥 3𝑎−1 𝑥 2 +3𝑥 4𝑥𝑦−3−2𝑦+6𝑥 9) 10) Дополнительные задания 1. Преобразуйте в дробь выражение: 1) 5) 𝑏−6 4−𝑏2 + 𝑎+4 𝑎2 −2𝑎 2 2𝑏−𝑏2 − 𝑎 𝑎2 −4 2) 6) 𝑥−12𝑎 𝑥 2 −16𝑎2 (𝑎+𝑏)2 𝑎2 +𝑎𝑏 − + 4𝑎 4𝑎𝑥−𝑥 2 (𝑎−𝑏)2 𝑎2 −𝑎𝑏 3) 7) 𝑏 𝑎𝑏−5𝑎2 4−𝑥 2 16−𝑥 2 − − 15𝑏−25𝑎 𝑏2 −25𝑎2 𝑥+1 𝑥+4 4) 8) 𝑎−30𝑦 𝑎2 −100𝑦 2 𝑥+1 𝑥 2 −𝑥 − − 10𝑦 10𝑎𝑦−𝑎2 𝑥+2 𝑥 2 −1 9) 3 + 2𝑏+1 𝑏+7 10) 1−4𝑏2 𝑎+3 𝑎2 −1 − 1 𝑎2 +𝑎 2. Выполните действия: 1) 5) 9) 𝑎2 +𝑏2 𝑎3 +𝑏 1 − 3 1 2𝑥−𝑏 + 2𝑦 2 +16 𝑦 3 +8 2) 𝑎+𝑏 6𝑏𝑥 + 𝑎2 −𝑎+1 𝑎2 3) 𝑎3 +1 6) 𝑏3 −8𝑥 3 − 1−𝑎 2 1 𝑝−𝑞 − 3𝑝𝑞 4) 𝑝3 −𝑞 3 7) 6𝑎3 +48𝑎 𝑎3 +64 3𝑎2 − 𝑎2 −4𝑎+16 8) 10) 𝑦+2 3. Преобразуйте в дробь выражение: 1) 4) 7) 4 𝑦+2 3 − 1 2𝑏−2𝑎 + 𝑦−2 1 + 𝑥−𝑦 𝑥 2 +𝑥𝑦+𝑦 12 2𝑏+2𝑎 − 2 2) 𝑦 2 −4 + 3𝑥𝑦 𝑥 3 −𝑦 𝑎2 𝑎2 𝑏−𝑏3 + 3 1 𝑥−𝑦 5) 8) 2𝑎+𝑏 2𝑎2 −𝑎𝑏 𝑎 𝑎−6 − − 16𝑎 4𝑎2 −𝑏2 3 𝑎+6 2𝑎2 +7𝑎+3 𝑎3 −1 + − − 2𝑎−𝑏 2𝑎2 +𝑎𝑏 𝑎2 6) 36−𝑎3 1−2𝑎 𝑎2 +𝑎+1 3) − 3 𝑎−1 9) 𝑥−2 𝑥 2 +2𝑥+4 1 (𝑎−3)2 1 𝑎−4𝑏 − − − 6𝑥 𝑥 3 −8 2 + 𝑎2 −9 1 𝑎+4𝑏 − + 1 𝑥−2 1 (𝑎+3)2 2𝑎 16𝑏2 −𝑎2 10) 4. Докажите тождество: 1) 6𝑥 𝑥+3 =6− 18 2) 𝑥+3 𝑎𝑥 𝑥+𝑏 5) 6) 9) 10) =𝑎− 𝑎𝑏 3) 4) 7) 8) 𝑥+𝑏 5. При каком значении а тождественно равны выражения: 1) 5) 9) 2𝑥 𝑥+3 2𝑥 3−𝑥 𝑥 𝑥−5 и2+ и 𝑎 3−𝑥 и1+ 𝑎 2) 𝑥+3 𝑥+2 5−𝑥 и 𝑎 5−𝑥 −1 6) −2 𝑎 3) 4) 7) 8) 10) 𝑥−5 6. Представьте дробь в виде суммы или разности целого выражения и дроби: 1) 6) 𝑥 2 −3𝑥+6 𝑥−3 −2𝑥 𝑥−1 2) 7) 𝑦 2 +5𝑦−8 𝑦+5 2𝑥 5−𝑥 3) 8) 𝑎2 +7𝑎+2 𝑎+6 𝑥−3 2−𝑥 4) 9) 3𝑏2 −10𝑏−1 𝑏−3 5) 5𝑥 𝑥+2 10)