ТЕОРИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ЗОНДА В ПЛАЗМЕ, ОБРАЗОВАННОЙ ПРОДУКТАМИ ЯДЕРНЫХ РЕАКЦИЙ

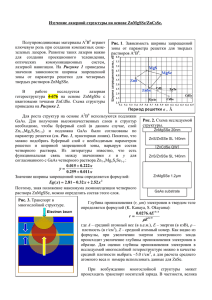
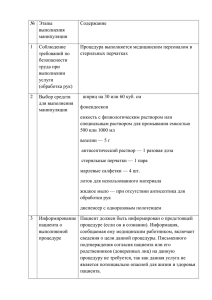
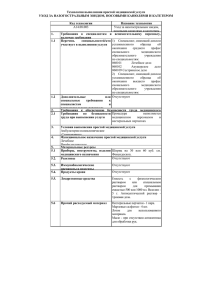
ТЕОРИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ЗОНДА В ПЛАЗМЕ, ОБРАЗОВАННОЙ
ПРОДУКТАМИ ЯДЕРНЫХ РЕАКЦИЙ
Кунаков С.К., Кудабаева А.Д., Шапиева А.Е.
Международный Университет Информационных Технологий
Республика Казахстан, Алма-Ата
[email protected]
В настоящей работе изложена теория сферического зонда в химически активной
слабоионизированной плазме, содержащей отрицательные ионы. Рассмотрен случай
интенсивной ионизации когда параметр, равный отношению ионизационной длины к
радиусу зонда, является малым. Предполагается, что дебаевский радиус мал по сравнению
с радиусом зонда,длина энергетической релаксации электронов много меньше локального
макроскопического масштаба и функция распределения электронов определяется
локальными значениями ne и Te.
1. Основные уравнения
Плазма, образованная продуктами ядерных реакций представлена плазмой
газовой смеси, 3He+UF6 ,находящейся в нейтронном потоке. Продукты ядерной реакции
3
He+n ® p+T+0.76 Mev вызывают образование положительных и отрицательных ионов и их
последующую рекомбинацию по следующим каналам:
3
3
He  n  p  T  0.76Mev
(1)
He  ( p, T )  He   e  ( p, T )e
3
(2)
He   2He 3 He 2  3He *
(3)
UF6  ( p, T )  UF6  ( p, T )e e
(4)
UF6  e  UF6 -
(5)
UF6  (UF6 , He 2 )  2UF6*  2 He
(6)
He 2  e  2He *
(7)


UF6  UF6  UF6*
(8)
Скорость ионизации определяется количеством тепловых нейтронов и ценой
образования пары ион-электрон Ω и равна:
𝑆=
𝑛 (3 𝐻𝑒)∗Φ∗𝜎𝑓 ∗𝐸0
(9)
Ω
где (3 𝐻𝑒) - концентрация нейтральных атомов гелия, Φ - величина нейтронного потока,
𝜎𝑓 - сечение реакции (1), 𝐸0 - кинетическая энергия продуктов реакции (1), Ω - цена
образования пары ион-электрон в газовой смеси 3He+UF6.
С учетом этих элементарных процессов (1-8) основные
гидродинамическом приближении для неподвижной плазмы имеют вид:
𝑑
(−𝐷+
𝑑𝑟
𝑑𝑛+
𝑑𝑟
𝑑𝜑
+ 𝑏 + 𝑛+ 𝑑𝑟 ) = 𝑆 − 𝑎𝑒 𝑛+ 𝑛𝑒 − 𝑎𝑖 𝑛+ 𝑛−
уравнения
в
(10)
𝑑
(−𝐷−
𝑑𝑟
𝑑
(−𝐷𝑒
𝑑𝑟
𝑑2 𝜑
𝑑𝑟 2
𝑑𝑛−
𝑑𝑟
𝑑𝑛𝑒
𝑑𝑟
𝑑𝜑
− 𝑏 − 𝑛− 𝑑𝑟 ) = 𝛽𝑛𝑒 − 𝑎𝑖 𝑛+ 𝑛−
(11)
𝑑𝜑
− 𝑏 𝑒 𝑛𝑒 𝑑𝑟 ) = 𝑆 − 𝑎𝑒 𝑛+ 𝑛𝑒 − 𝛽𝑛𝑒
(12)
= 𝑛+ − 𝑛− − 𝑛𝑒
(13)
где 𝑛+ , 𝑛− , 𝑛𝑒 - концентрации положительных, отрицательных ионов и электронов,
𝐷+ , 𝐷− , 𝐷𝑒 , 𝑏 + , 𝑏 − , 𝑏 𝑒 - коэффициенты диффузии и подвижности положительных,
отрицательных ионов и электронов, 𝛽 - константа прилипания [2], определяющая
формирование отрицательных ионов (5).
Рекомбинация атомарных ионов гелия равна:
𝛼 = 2 ∗ 10−27 𝑛𝑒 𝑐𝑚3 /𝑠
(14)
Рекомбинация молекулярных ионов гелия равна [3]:
𝑇
3
𝑒
𝛼𝑖 = 10−(26±1) (300
)2 𝑐𝑚6 /𝑠
(15)
Граничные условия на поверхности зонда определяются следующими условиями:
𝑛+ (𝑟𝑝 ) = 𝑛− (𝑟𝑝 ) = 𝑛𝑒 (𝑟𝑝 ) = 0, 𝜑(𝑟𝑝 ) = 𝜑𝑝
𝑛+ (𝑟0 ) = 𝑛+0 , 𝑛− (𝑟0 ) = 𝑛−0 , 𝑛𝑒 (𝑟0 ) = 𝑛𝑒0 0, 𝜑(𝑟0 ) = 0
(16)
(17)
где 𝑟𝑝 - радиус зонда, 𝑟0 - радиус слоя объемного заряда.
В невозмущенной области (𝑟 ≥ 𝑟0 )𝑛−0 = (1 − 𝛿)𝑛+0 , 𝑛𝑒 = 𝛿𝑛+0 , а 𝛿 и 𝑛+0 определяются
следующими уравнениями:
𝛽
𝑆
𝛽𝑆
(𝑛+0 )3 + 𝛼 (𝑛+0 )2 − 𝛼 𝑛+0 − 𝛼
𝑒
𝑒 𝛼𝑖
𝑒
=0
𝛼 𝑛+0
𝑖
𝛿 = 𝛽+𝛼
𝑛+0
(18)
(19)
𝑖
Во всех точках от зонда до противозонда выполняется соотношение:
𝐽+ − 𝐽− − 𝐽𝑒 = 0
(20)
𝐽𝑝 = 𝑒𝐽+ + 𝑒𝐽− + 𝑒𝐽𝑒
(21)
Тогда напряженность электрического поля равна:
𝑑𝜑
𝑑𝑥
𝐷 + −(1−𝛿)𝐷 − −𝛿𝐷 𝑒 𝑑𝑙𝑛(𝑛+ )
= −( 𝑏++(1−𝛿)𝑏−+𝛿𝑏𝑒 )
𝑑𝑥
(22)
При этом диффузионные потоки могут быть представлены в следующем виде:
𝐽+ = −𝐷𝑎+
𝐽− = −𝐷𝑎−
𝐽𝑒 = −𝐷𝑎𝑒
𝑑𝑛+
𝑑𝑥
𝑑𝑛−
𝑑𝑥
𝑑𝑛𝑒
𝑑𝑥
(23)
(24)
(25)
где 𝐷𝑎+ , 𝐷𝑎− , 𝐷𝑎𝑒 - коэффициенты амбиполярной диффузии заряженных компонентов:
𝐷𝑎+ =
𝛿(𝐷 + 𝑏 𝑒 +𝐷 𝑒 𝑏+ )+(1−𝛿)(𝐷 + 𝑏 − +𝐷 − 𝑏+ )
(26)
𝑏 + +(1−𝛿)𝑏 − +𝛿𝑏 𝑒
(𝐷 + 𝑏 − +𝐷 − 𝑏 + )+𝛿(𝐷 + 𝑏 𝑒 +𝐷𝑒 𝑏 + )
𝐷𝑎− =
(27)
𝑏 + +(1−𝛿)𝑏 − +𝛿𝑏 𝑒
(𝐷 + 𝑏 𝑒 +𝐷 𝑒 𝑏+ )
𝐷𝑎𝑒 = 𝑏++(1−𝛿)𝑏−+𝛿𝑏𝑒
(28)
Вольтамперная характеристка зонда может быть получена в любом сечении, как в
области объемного заряда, так и в диффузионной области, разница состоит в том, что в
слое объемного заряда ток формируется за счет переноса вследствие действия
электрического поля на заряженные частицы, в то время как в диффузионной области
диффузионный поток уравновешивает процессы ионизации, которые в свою очередь не в
полной мере компенсируются рекомбинационными процессами, как это есть в области
невозмущенной плазмы. Более того рекомбинационные процессы и процессы образования
отрицательных ионов по мере приближения к зонду уменьшаются вследствие падения
концентрации электронов в случае отрицательного потенциала зонда и разогрева
электронов в случае положительного потенциала зонда.
В нормализованном виде уравнения (10-13) и граничные условия (16-17) имеют
следующий вид:
𝑑
𝜔 𝑑𝜉 (−
𝑑
𝜔 𝑑𝜉 (−
𝑑
(−
𝑑𝜉
𝜒𝜀
𝑑𝜉
𝑑𝑁 −
𝑑𝜉
𝑑𝑁 𝑒
𝑑2 𝜓
𝑑𝜉
𝑑𝑁 +
𝑑𝜉
𝜒
𝑑𝜓
𝜒
𝑑𝜓
+ 𝜏 𝑁 + 𝑑𝜉 ) = 1 − 𝛼𝑖 𝑁 + 𝑁 − − 𝛼𝑒 𝑁 + 𝑁 𝑒
(29)
+ 𝜏 𝑁 − 𝑑𝜉 ) = 𝛽𝑒 𝑁 𝑒 − 𝛼𝑖 𝑁 + 𝑁 −
+ 𝜒𝑁 𝑒
𝑑𝜓
𝑑𝜉
(30)
) = 1 − 𝛽𝑒 𝑁 𝑒 − 𝛼𝑒 𝑁 + 𝑁 𝑒
(31)
= 𝑁+ − 𝑁− − 𝑁𝑒
(32)
Граничные условия соответственно преобразуются к следующему виду:
𝑁 + (1) = 0, 𝑁 − (1) = 0, 𝑁 𝑒 (1) = 0, 𝜓(1) = 1
(33)
𝑁 + (𝜉0 ) = 1, 𝑁 − (𝜉0 ) = 1 − 𝛿, 𝑁 𝑒 (𝜉0 ) = 𝛿, 𝜓(𝜉0 ) = 0
(34)
В уравнениях (29-32) были использованы следующие обозначения:
𝜔=
𝐷+ 𝑛+0
𝑟𝑑 2
𝛽𝑛+0
𝛼𝑒 (𝑛+0 )2
𝛼𝑖 (𝑛+0 )2
𝑟
𝜑
,
𝜀
=
(
)
,
𝛽
=
,
𝑎
=
,
𝑎
=
,𝜉 = ,𝜓 =
,
𝑒
𝑒
𝑖
2
𝑆𝑟𝑝
𝑟𝑝
𝑆
𝑆
𝑆
𝑟𝑝
𝜑𝑝
𝜑𝑝
𝑛+
𝑛−
𝑛𝑒
𝐾𝑇𝑒
𝑇
−
𝑒
+
𝑁 = +0 , 𝑁 = +0 , 𝑁 = +0 , 𝑟𝑑 =
, 𝜏 = , 𝑛+0 = 𝑛∞
, 𝜒 = 𝐾𝑇𝑒
2
+0
𝑛
𝑛
𝑛
4𝜋𝑒 𝑛
𝑇𝑒
+
𝑒
2. Слой объемного заряда
В случае отрицательных потенциалов зонда система уравнений (29-32)
преобразуется к следующему виду:
𝑑
𝑑𝜉
𝑑𝜓
(𝜏𝑁 + 𝑑𝜉 ) = 1
(35)
𝑑 𝑑𝜓
𝜀 𝑑𝜉 𝑑𝜉 = 𝑁 +
(36)
Система (35-36) может быть приведена к дифференциальному уравнению
относительно 𝜓(𝜉):
𝑑
𝑑𝜉
(𝜓′′ 𝜓 ′ ) =
𝜏
(37)
𝜔𝜒2 𝜀
Величина электрического поля в слое 𝑟𝑝 → 𝑟0 равна:
1
𝜓′ = 𝜓′ 0 √1 +
где 𝜃 =
𝜀𝜔𝜒2
𝜏
2𝜃(𝜓′ 0 )
2
(𝜉 − 𝜉0 )2
(38)
.
3. Диффузионный слой
В диффузионном слое для отрицательного потенциала зонда концентрация
положительных ионов определяется следующим уравнением:
𝜔
где 𝜔 =
𝐷 + 𝑛+0
𝑆𝑟𝑝2
𝑑2 𝑁 +
𝑑𝜉 2
= 1 − 𝑎(𝑁 + )2
2
,𝑎 =
𝛼𝑒 𝛿(𝑛+0 ) +𝛼𝑖 (1−𝛿)(𝑛+0 )
(39)
2
𝑆
Определяя величину градиента концентрации на границе слой объемного заряда диффузионный слой можно определить зондовый ток на зонд:
𝐼𝑝 = 4𝜋𝑒 (1 +
𝑏+
+ +0 2 1
)
𝐷
𝑛 𝑟0 𝑟
𝑎
−
𝑒
𝑏 +𝑏
𝑝
2
𝑎
{𝜔 (1 − 3 − 𝑁0 +
𝑎𝑁03
3
1
2
)}
(40)
Здесь как и в работе [4]
Λ
1
𝑟
2
𝑁0 = ( 𝐾𝑇𝑒 )3 ( 𝑟𝑑 )3
𝑒
(41)
𝑝
а величина слоя объемного заряда равна:
𝑟0 =
3𝐷𝑎+ 𝑛+0 𝑁0 2
𝑆𝑟𝑝
Λ=
2
𝑎
{ (1 − 3 − 𝑁0 +
𝜔 𝜔
𝐷 + −(1−𝛿)𝐷 − −𝛿𝐷 𝑒
𝑏 + +(1−𝛿)𝑏 − +𝛿𝑏 𝑒
𝑎𝑁03
3
1
2
)}
(42)
(43)
Литература:
1. S.K.Kunakov and E.E.Son Probe Diagnostics of Nuclear-Excited Plasma of Uranium
Hexafluoride, High Temperature, 2010, Vol.48, No.6, pp.789-805, Pleades Publishing, Ltd, 2010
2. R.N.Compton On the formation of positive and negative ions in gaseous UF_{6}.The Journal
of Chemical Physics,Vol.66, No.10, 15 May 1977, pp. 4478-4485.
3. H.A.Hassan and Jerry E.Deese Electron distribution function in a plasma generated by fission
fragments, The Physics of Fluids, Vol.19.,No.12, December 1976,pp.2005-2010.
4. К.Н.Ульянов Теория электрических зондов в плотной плазме, ЖТФ, Том XL, №4, стр
790-798.