Дистанционная олимпиада по физике 9 класс (1 тур). Ученица 9
реклама

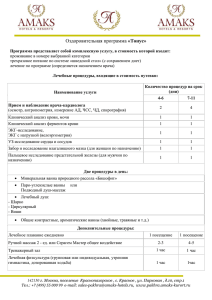
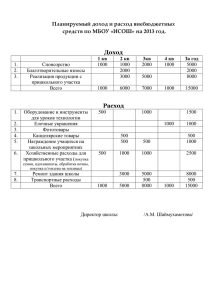
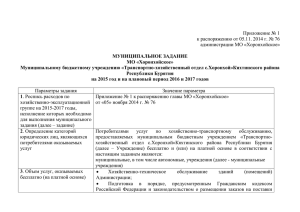
Дистанционная олимпиада по физике 9 класс (1 тур). Выполнила: Фазлыева Элина Маратовна Ученица 9Б класса МБОУ СОШ № 4 г. Туймазы Учитель физики: Никитина Наталья Викторовна ЗАДАЧА №1. Решение: F1 B A l2 l1 F2 C F1*l1=F2*l2 F1=FА=ρв*V*g F2=FА= ρв*V*g l1=AB*cosα l2=AC* cosα 𝑙1 𝐴𝐵 ∗ 𝑐𝑜𝑠𝛼 = =2 𝑙2 𝐴𝐶 ∗ 𝑐𝑜𝑠𝛼 ρв*V1*g*l1= ρв*V*g*l2 2*V1=V 1 V1= *V 2 h=0 Центр левого шара находится на высоте 0 независимо от глубины правого, т.к. 𝑙1 𝑙2 = 2. Это справедливо до тех пор пока рычаг может поворачиваться. ЗАДАЧА №2. с Решение: Объём параллелепипеда: V=c2 * b Из него вычтем ту часть, которая находится в отверстии. Найдём объём части параллелепипеда, погружённый в жидкость при полном заполнении. с V1 a c с 1 V2= *a2*b 4 1 1 V1=V-V2=c2*b - *a2*b= b*(c2 - *a2) 4 4 1 FA= ρ*V1*g = ρ*b*(c - *a )*g 2 4 FA=Fтяж. Fтяж.=M*g 1 M= ρ*b*(c2 - *a2) 4 𝟏 ОТВЕТ: M= ρ*b*(c2 - *a2). 𝟒 2 ЗАДАЧА №3. R1 Решение: Когда R=0, это равносильно тому, что точки a и b замкнуты, тогда схема преобразуется в такой вид: R2 R a R2 b R1 R1 R2 R2 R1 Найдём общее сопротивление цепи. R параллельных участков: R1,2 = Rо = 2* 𝑅1 ∗𝑅2 𝑅1 + 𝑅2 ; 𝑅1 ∗𝑅2 𝑅1 + 𝑅2 По закону Ома найдём общее сопротивление взяв данные из графика и условия задачи. Rо= 𝑈 𝐼о = 3 1∗10−3 = 3 ∗ 103 Ом При R стремящемся к бесконечности сила тока стремится к 0,75 мА А это равносильно к разрыву точек a и b. Тогда схема преобразуется в следующий вид: Rо2 = R1 R2 Rо2 = 𝑅1 +𝑅2 2 R2 R1 𝑅1 +𝑅2 2 𝑈 𝐼2 = ; 3 = 0,75∗10−3 3 0,75 ∗ 103 = 3 0,75 ∗ 103 Ом Решим систему уравнений: 𝑅1 ∗𝑅2 𝑅1 + 𝑅2 = 3 * 103 2 𝑅1 + 𝑅2 = 𝑅1 ∗𝑅2 𝑅1 + 𝑅2 6 0,75 * 103 = 1500 𝑅1 + 𝑅2 = 8000 R1=8000 – R2 (8000− 𝑅2 )∗ 𝑅2 8000 = 1500 *8000 8000*R2 - R22 = 12000000 - R22 + 8000*R2 – 12000000 = 0 *(-1) R22 - 8000*R2 + 12000000 = 0 D= 80002 – 4*12000000 = 64000000 – 48000000=16000000 = 40002 8000−4000 R2(1) = R2(2) = = 2000 (Ом) 2 8000+4000 2 = 6000(Ом) Найдём: R1(1) = 8000 – R2(1) = 8000 – 2000 = 6000 (Ом) R1(2) = 8000 – R2(2) = 8000 – 6000 = 2000 (Ом) R1=6000 Ом или R1=2000 Ом R2=2000 Ом R2=6000 Ом ОТВЕТ: R1=6000 Ом, R2 = 2000 Ом ; R1 = 2000 Ом, R2 = 6000 Ом. ЗАДАЧА №4. S h1 h2 S1 S2 Решение: Т.к. высоты обратно пропорциональны расстояниям, то h1 h2 = 1,5 = S2 S1 S2=S-S1 S−S1 1) S1 = 1,5 Через 100 м: 2) S1 +100 S−S1 −100 S1 +100 S2 −100 = 1,5 = h2 h1 = 1,5 Решим систему: S−S1 = 1,5 S1 S1 +100 S−S1 −100 = 1,5 S – S1 = 1,5*S1 S = 2,5*S1 S1 = S 2,5 S 2,5 S S 2,5 + 100 = 1,5*(S + 100 = 1,5*S – - 1,5∗S + 1,5∗S 2,5 1 2,5 S−3,75∗S+1,5∗S S - 100) 2,5 1,5∗S 2,5 - 150 = - 150 – 100 = - 250 2,5 −1,25 ∗ S = −250 2,5 -1,25*S = -250*2,5 -1,25*S = -625 S=500 м ОТВЕТ: S=500 м ЗАДАЧА №5. 1)ДАНО: t0=0°C РЕШЕНИЕ: Скорость поступающей теплоты обозначим q. mл = mв q= 2 τ1=2 ч 40 мин =2 ч 3 св = 4200 Дж кг∗°C 5 Дж λл = 3,2*10 кг Q1 τ ; Q1 = λл* mл ; Q = c*m* Δt ; Q2 = cв*2*mв*1 ; Q1 τ1 * τ2 = cв*2*mв*1 ; τ2 = τ2 = cв ∗2∗mв ∗1∗ τ1 λ л ∗ mл 2 3 4200∗2∗2 3,2∗105 = 2* св λл ∗ τ1 ; = 0,07 ч НАЙТИ: τ2 ОТВЕТ: τ2 = 0,07 ч 2)Т.к. разность температур 21°C - 20°C = 1°C, время нагревания должно быть такое же, но в реальности, чем меньше разность температур между окружающим воздухом и телом(водой) теплопередача происходит медленнее, значит время на нагрев будет больше. ЗАДАЧА №6. ДАНО: РЕШЕНИЕ: I1=2 A Мощность на реостате: Р=Uр*I = I2*Rр , где Rр- сопротивление P1=48 Вт реостата, Uр- напряжение на реостате. I2=5 A P2=30 Вт Rр(2)=0 Ом R Rр НАЙТИ: 1)Сопротивление реостата: RP1 = P2 U-? R-? I3-? Rm-? P1 RP2 = I22 I21 = = 30 25 48 4 = 12 Ом = 1,2 Ом Общее сопротивление: Rо = R+Rp U = I1*(R+RP1) U = I2*(R+RP2) I1*(R+RP1) = I2*(R+RP2) 2*(R+12) = 5*(R+1,2) 2*R+24 = 5*R+6 R = 6 Ом U = 2*(6+12) = 36 В 2) I3 = U R = 36 6 =6А 3) Рp=Up*I = I2*Rp , т.к. I = U R+Rр Рp = U2 ∗ Rр (R+Rр )2 Надо найти наибольшее значение Pp , где переменной будет Rp. Она зависит от соотношения R и Rp Попробуем подставить R=R p: P1 = 362 ∗6 (6+6)2 = 1296∗6 144 = 1296 24 = 54 Вт Попробуем подставить 2R= R p: P2 = 362 ∗12 (12+6)2 = 1296∗12 324 = 288 Вт Попробуем подставить 3R= R p: P3 = 362 ∗18 (18+6)2 = 1296∗18 576 = 40 Вт Вывод: при 2R= R p выделится наибольшая мощность. ОТВЕТ: U=36 В ; R=6 Ом; I3=6 А ; Rm=12 Ом ЗАДАЧА №7. υ0y hmax υ0x РЕШЕНИЕ: H max=h max υ0y = υ0*sinα0 υ0x = υ0*cosα υy=0 в верхней точке υy= υ0y – g*t t= h=h0+ υ0y*t – 0=H+ υ0y2 g υ0y g g∗t2 - 2 υ0y2 H= 2∗g υ0y2 2∗g υ0y = √2 ∗ g ∗ H sinα0 = √2∗g∗H υ0 α Если α ≥α0 , мальчик может попасть в птицу. υ0x = υ0*cosα υптицы > υ0*cosα0 В этом случае мальчик ни при каком угле не попадёт в птицу. ЗАДАЧА №9. ДАНО: РЕШЕНИЕ: U1=380 В Q = A = U*I*t ; заменим I = U2=220 В Q1 = U3=127 В Q1 = t1=2 мин=120 с ΔQ t2=10 мин=600 с tн=0°C 3802 𝑅 17328000 = Дж ; Q2 = 𝑅 12242400 𝑅 2222 Q= R U2 ∗ 600 ; Q3 = 𝑅 29570400 𝑅 Дж это потери за 1 с 𝑅 ∗ t3 = Q1 + ΔQ Δt ΔQ Δt = * Δt2 t3 = t1+ Δt2 1272 𝑅 ∗ (t1+ Δt2) = 17328000 𝑅 + 𝑅 ∗ t3 Дж = 600-120 = 480 c Δt2 = t3 – 120 c 1272 ∗t R 1272 Δt 1 Q3 = НАЙТИ: t3 ∗ 120 ; Q2 = U 12242400 𝑅 ∗ 480 * Δt2 12242400 Дж 𝑅 ∗ 480 𝑐 1272*(120 + Δt2) = 17328000 + 12242400 480 * Δt2 1935480 + 16129 * Δt2 = 17328000 + 25505 * Δt2 1935480 – 17328000 = Δt2*(25505 – 16129) Δt 2 = 15392520 9376 = 1641,7 с t3 = 120 + 1641,7 = 1761, 7 с = 29 мин ОТВЕТ: t3=29 мин ЗАДАЧА №10. S2 З2 S З1 Сектор, в котором увидим изображение S2 во втором зеркале. З2 S З1 S1 Сектор, в котором увидим изображение S1 в первом зеркале. S2 З2 S З1 S1 Общий сектор, в котором увидим изображения в обеих зеркалах.