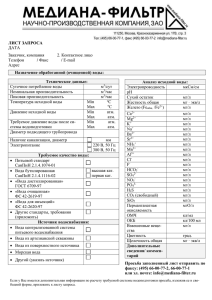
7139. = 228 мм = 180 мм h
реклама

7139. В трех одинаковых сообщающихся сосудах находится ртуть. В левый сосуд
налили слой воды высотой h1 = 180 мм, а в правый - высотой h3= 228 мм. На какую
величину h2 сместится уровень ртути в среднем сосуде, если известно, что ртуть из
левого и правого сосудов не вытесняется водой полностью? Плотность ртути
ρ=13,6г/см3, плотность воды ρв=1г/см3.
Дано: h1 = 18,0 см; h3= 22,8 см; ρ=13,6г/см3,ρв=1г/см3
Найти: h2=?
Решение. Введем обозначения:h2 — высота ртути в
среднем сосуде над начальным уровнем АВ, h1 —
высота воды в левом сосуде над уровнем CK, h3 —
высота воды в правом сосуде над уровнем DE.
Так как на уровне CK однородная жидкость
(ртуть), то давления в точках C, K будут равны.
𝑝𝐶 = 𝜌в ∙ 𝑔 ∙ ℎ1 + 𝑝атм ,
𝑝𝐾 = 𝜌 ∙ 𝑔 ∙ (ℎ2 + ∆ℎ1 ) + 𝑝атм .
Δh1 – понижение уровня ртути в левом сосуде.
На уровне DE
𝑝𝐷 = 𝜌 ∙ 𝑔 ∙ (ℎ2 + ∆ℎ1 + ∆ℎ2 ) + 𝑝атм ;
𝑝𝐸 = 𝜌в ∙ 𝑔 ∙ ℎ3 + 𝑝атм .
Так как жидкость (ртуть) несжимаема, то увеличение объема ртути в среднем сосуде
ΔV2 равно суммарному уменьшению объемов ртути в боковых сосудах, т.е.
∆𝑉2 = ∆𝑉1 + ∆𝑉3
Или
ℎ2 = ∆ℎ1 + ∆ℎ3 = 2 ∙ ∆ℎ1 + ∆ℎ2
где h2 — изменение уровня ртути в среднем сосуде, Δh1 — изменение уровня ртути в
левом сосуде, Δh1+Δh2 — изменение уровня ртути в правом сосуде
Решим систему трех уравнений с тремя неизвестными (h2, Δh1, Δh2):
ℎ2 = 2 ∙ ∆ℎ1 + ∆ℎ2 , (1)
𝜌в ∙ 𝑔 ∙ ℎ1 + 𝑝атм = 𝜌 ∙ 𝑔 ∙ (ℎ2 + ∆ℎ1 ) + 𝑝атм , (2)
𝜌в ∙ 𝑔 ∙ ℎ3 + 𝑝атм = 𝜌 ∙ 𝑔 ∙ (ℎ2 + ∆ℎ1 + ∆ℎ2 ) + 𝑝атм ,
(3)
{ 𝜌в ∙ 𝑔 ∙ ℎ1 + 𝜌 ∙ 𝑔 ∙ ∆ℎ2 + 𝑝атм = 𝜌в ∙ 𝑔 ∙ ℎ3 + 𝑝атм . (4)
Решая, получим,
𝜌
из (4) ∆ℎ2 = в ∙ (ℎ3 − ℎ1 ),
из (2) ∆ℎ1 =
из (1)
𝜌
𝜌в
𝜌
∙ ℎ1 − ℎ2 ,
𝜌в
𝜌в
ℎ2 = 2 ∙ ( ∙ ℎ1 − ℎ2 ) + ∙ (ℎ3 − ℎ1 ),
𝜌
𝜌
𝜌в
𝜌в
ℎ2 = 2 ∙ ∙ ℎ1 − 2 ∙ ℎ2 + ∙ (ℎ3 − ℎ1 ),
𝜌
𝜌
𝜌в
𝜌в
3 ∙ ℎ2 = 2 ∙ ∙ ℎ1 + ∙ (ℎ3 − ℎ1 ),
𝜌
𝜌
𝜌в
(ℎ + ℎ3 )
ℎ2 =
3∙𝜌 1
Ответ.
𝒉𝟐 =
𝝆в
(𝒉 + 𝒉𝟑 ),
𝟑∙𝝆 𝟏
𝒉𝟐 = 𝟏𝟎 мм.