Целые уравнения с параметрами рс
реклама

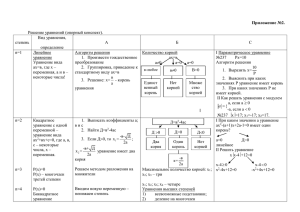
Решение заданий с параметрами в курсе основной школы. I. Целые уравнения с параметрами. 1) Решим уравнение 8х = 7, 15х = 7, -11х = 7, 0х = 7. Корень первого уравнения число 7/8, второго число 7/15, третьего - число -7/77, четвертое уравнение корней не имеет. Каждое из данных уравнений имеет вид ах = 7. В зависимости от а возникают разные случаи: если а≠ 0, то уравнение имеет корень 7/а, если а = 0, то уравнение не имеет корней. Рассматривая уравнение ах = 7, мы придавали буквам а и х разный смысл считая, что буквой х обозначено неизвестное число, а буквой а - некоторое фиксированное число, значение которого в каждом конкретном случае известно. В таких случаях говорят, что а является параметром, а уравнение называют уравнением с параметром. 2) С понятием параметра учащиеся встречаются при рассмотрении вопроса о корнях линейного уравнения ах =b с одним неизвестным, хотя сам термин «параметр» не вводился. Параметрами в данном уравнении служили буквы а и b . При выводе формулы корней квадратного уравнения ах2 + bх + с = 0 параметрами считались его коэффициенты а, b и с. При изучении линейной функции у = kx + b за параметр принимались коэффициенты k и b. Рассматривая уравнение ах = 7, мы выделили случаи когда а ≠0 и когда а =0, и установили, что при а ≠ 0 уравнение имеет корень 7/а, а при а = 0 уравнение не имеет корней. Таким образом, мы установили, как можно найти корень уравнения при любом значении а. в таких случаях говорят, что мы решили уравнение с параметром а. Вообще решить уравнение с параметром - это значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество корней. Рассмотрим примеры. Пример 1. Решим уравнение а х - 2 х = а 2 + а - 6 . Решение. Вынесем множитель за скобки: (а - 2)х = а2 + а - 6 . Имеем линейное уравнение, число корней которого зависит от того, равен ли нулю коэффициент при х или отличен от нуля. Если а - 2 ≠ 0, т.е. а ≠ 2, то уравнение имеет единственный корень X= 𝑎2 +𝑎−6 𝑎−2 (𝑎−2)(𝑎+3) x= 𝑎−6−2 =𝑎+3 Если а = 2, то уравнение принимает вид 0х = 0. В этом случае любое число является корнем уравнения. Ответ: а = 3, если а ≠ 2; любое число, если а = 2. Пример2.Решим уравнение относительно х р2х - 3 р х = р 2 - 9 , (р2 - 3р)х = р2 - 9 Если р2 - 3р ≠ 0, т.е. р ≠ 0, р ≠ 3, то уравнение имеет единственный корень х= 𝑝2 −9 = 𝑝2 −3𝑝 𝑝+3 𝑝 Если р = 0, то уравнение примет вид 0х = -9, значит уравнение не имеет корней. Если р = 3, то уравнение примет вид 0х = 0,тогда любое число является решением уравнения. Ответ: любое число, если р = 3; нет корней, если р = 0;p = 𝑝−3 𝑝 ,если р≠0 и р≠3. Аналогично решаются следующие уравнения: ах = а + 6; с(с-2)х = с 2 - 4 ; ах + 5а = 6х; а х + 8 х = а 2 + 6 а - 16: сх + х(2-5с) = 1 - 2с; (а2 + 1)х + а(а -2х) = 1 и т.д. Пример 3. При каких значениях параметра р уравнение (Зх + р + 2)2 - ( З х - р + 1 ) 2 = 12х + 4 имеет: а) отрицательный корень. б) корень, принадлежащий промежутку (-0,5; 0,5)? Решение: Преобразуем левую часть, используя формула разности квадратов, т.е. (Зх + р + 2 - З х + р - 1 ) ( З х + р + 2 + З х - р + 1) = 12х + 4, (2р + 1) (6х + 3) = 12х + 4, 12рх + 6р + 6х +3 = 12х + 4, х (12р - 6) = 1 - 6р, Если р ≠1/2 , то х = 1−6р 12р−6 единственный корень. а) чтобы найти при каких значениях параметра р уравнение имеет 1- 6р отрицательный корень, решим неравенство ------ — <0 12 р - 6 Итак, уравнение имеет отрицательный корень, если р 𝜖 (- ∞;-1/6) ∪ (1/2; +∞) б)чтобы найти при каких значениях параметра р уравнение имеет корень, принадлежащий промежутку (-0,5;0,5) решим двойное неравенство: − 1 1 − 6р 1 < < 2 12р − 6 2 Данное неравенство равносильно системе неравенств 1 − 6р 1 < 12р − 6 2 1 − 6р 1 >− 12р − 6 2 - + 1/3 1 ½ р Решив эту систему получим р<1/3. ½ р Ответ: а) при р𝜖(-∞;1/6)∪(1/2;+∞) б) при р<1/3. Пример 4. При каких значениях параметра а уравнение 3х2 + (2а +3) = a =2=0 имеет два корня. Решение: Уравнение имеет два корня, если D>0. Найдём дискриминант: D=(2а+3)2-4*3(а+2)=4а2-15. 15 D>0 при 4а2+5>0 ⇔|a|> 15 15 2 Ответ :при а> , a<- . 2 2 Пример 5.Решить относительно х уравнение х2+4а=0 Решение: Если а = 0, то х2=0, х=0 – данный корень уравнения. Если а<0, то х2=-4а, х= ∓√−4а. Если а>0, то уравнение х2+4а = 0 не имеет корней Ответ: ∓√−4а, если а<0, 0, если а=0; нет корней, если а>0. Пример 6. Решить уравнение относительно х. px2+16=4x2-p2 Решение : px2+16=4x2-p2 px2- 4x2=p2-16 (р-4)х2 = р2-16 Если р-4≠0 и р>-4, то х2 = р2 −16 р−4 =р+4 х=−√р − 4 х=√р + 4 Если р=-4, то х=0 – единственный корень Если р=4, 0х2=0, то х- любое число Если р<-4 , то уравнение не имеет корней Ответ: =−√р − 4 ; √р + 4, если р>-4; нет корней, если р<-4, любое число, если р=4; 0, если р=-4. Пример 7. Решить квадратное уравнение с параметром b 3х2-6х + b=0 Решение: Найдём дискриминант этого уравнения D=36 – 12b Рассмотрим случаи когда D>0, D=0, D<0. Пусть 36 – 12b<0, т.е. 12b<36, b<3, в этом случае уравнение имеет два корня: x= 6−√36−12𝑏 6 x= 6+√36−12𝑏 6 6 Если 36-12b = 0, т.е. b=3, то уравнение имеет единственный корень х= =1 3∙2 Если 36-12b <0, т.е. b>3, то уравнение не имеет корней. 6−√36−12𝑏 6+√36−12𝑏 Ответ: x= x= 6 1, если b=3, Нет корней, если b>3. 6 , при b>0; II. Дробно-рациональные уравнения. Чтобы решить дробно-рациональное уравнение с числовыми коэффициентами, умножают обе части на общий знаменатель дробей, входящих в уравнение, решают полученное целое уравнение и исключают из его корней, те, которые обращают в нуль общий знаменатель дробей. Аналогичным способом поступают при решении дробно-рациональных уравнений с параметрами. Пример. Решить относительно х уравнение. 4 𝑏 − =2 𝑥−3 2 Решение: Умножим обе части уравнения на общий знаменатель дробей, т.е. на выражение 2(х-3)≠0 Получим уравнение 8-bx+3b=4x-12, (4+b)x=20+3b Если 4+b=0, то b=-4, то полученное уравнение не имеет корней, а, значит, не имеет корней и заданное дробно-рациональное уравнение. Если 4+b ≠0, то b≠-4, то полученное уравнение имеет единственный корень 20+3𝑏 х= 4+𝑏 20+3𝑏 Из условия 4+𝑏 = 3 находим, что таких значений нет. 20+3𝑏 Итак, если b≠-4, то заданное уравнение имеет единственный корень х= если b=-4, то уравнение не имеет корней. 20+3𝑏 Ответ: , при b≠-4; корней нет, при b=-4. 4+𝑏 Пример. Решим уравнение 2𝑥 2𝑥+𝑎 – 𝑎−2 2𝑥−𝑎 - 4𝑎−2𝑎2 4𝑥 2 −𝑎2 4+𝑏 ,а =0 Решение Умножив обе части уравнения на общий знаменатель дробей и выполнив приведение подобных членов, получим квадратное уравнение 4x2 – 4(a-1)x + a2-2a = 0,где 2х+а≠ 0 а а−2 2х-а≠ 0ю Решив его найдём, что х1= , х2 = . 2 2 Первый корень не удовлетворяет исходному дробно-рациональному уравнению, а так как при х= ,общий знаменатель дробей, входящих в уравнение, обращается в 2 нуль. Остаётся выяснить, при каких значениях а второй корень является посторонним для данного уравнения. Подставив в равенство 4х2-а2=0 вместо х а−2 выражение , получим а = 1 Это значение а нужно исключить. 2 а−2 Итак при а ≠ 1 заданное уравнение имеет единственный корень х= , а при 2 а = 1 уравнение не имеет корней. Ответ: а−2 2 ,при а ≠ 1; нет корней при а=1. Пример . Найти, при каких значениях параметра а уравнение ах = 3х−1 а + 3х 3 имеет два корня, каждый из которых принадлежит промежутку (-1;1). Решение. Умножив обе части уравнения на 3х и выполнив преобразования получим уравнение 3ах2- (а+3)х + 1=0, где х≠0. Это уравнение имеет два корня, если а≠ 0, при D>0. Так как D=(а+3)2 – 12а=(а+3)2 , то D>0при а≠ 3. При а≠ 0 и а≠ 3 1 1 Рассматриваемое целое уравнение имеет корни х1= и х2 = . Оба эти корня 3 а удовлетворяют дробно-рациональному уравнению. Первый корень принадлежит промежутку (-1;1). Второй корень принадлежит этому промежутку при значениях а, удовлетворяющих системе : -1<1/а<1 а≠ 3 а≠ 0 Множеством решений этой системы является объединение промежутков (-1;0)∪ (0; 1) Ответ: при а∈(-1;0)∪ (0; 1). ху Пример . Решить уравнение = у − 1. х+1 а) относительно х б)относительно у Решение ху а) = у − 1, где у – параметр. х+1 ху = ху – х+у -1, если х+1≠0, т.е. х≠ −1 х = у -1 Исключим те значения у при которых х = -1, т.е. х- 1 =-1, у = 0. Ответ: у-1,если у≠ 0; нет корней при у=0. ху б) = у − 1, х – параметр х+1 ху = ху – х+у -1, если х+1≠0, т.е. х≠ −1 Итак, у = х +1, при х≠ -1; корней нет при х=-1. Ответ: х+1, при х≠ -1; корней нет при х=-1. 1. 2. 3. 4. Литература: В.Н.Литвиненко, А.Г.Мордкович «Практикум по решению математических задач». К.Петров «Сборник задач по алгебре» Л.И.Звавич, А.Р.Рязановский «Задачник для классов с углубленным изучением математики» М.И.Сканави «Сборник задач по математике для поступления в ВУЗы»