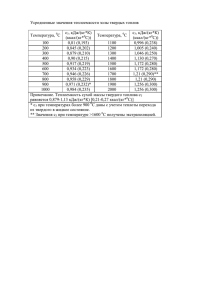
1 - Томский политехнический техникум

Областное государственное бюджетное
профессиональное образовательное учреждение
(ОГБПОУ «ТПТ»)
Практические работы по термодинамике
и методические указания по их выполнению
для студентов специальностей 21.02.01 «Разработка и эксплуатация
нефтяных и газовых месторождений» и 21.02.02 «Бурение нефтяных и
газовых скважин» заочной формы обучения
Автор: А.В.Ти
2015 г.
Пояснительная записка
Дисциплина «Термодинамика» входит в состав профессиональных модулей: ПМ.02
«Обслуживание и эксплуатация бурового оборудования», МДК.02.01 «Эксплуатация бурового
оборудования» для специальности 21.02.02 и ПМ.02 «Эксплуатация нефтегазопромыслового
оборудования», МДК.02.01 «Эксплуатация нефтегазопромыслового оборудования» для
специальности 21.02.01.
В результате изучения дисциплины студенты должны знать:
- основные понятия, законы и процессы термодинамики и теплопередачи;
- методы расчета термодинамических и тепловых процессов;
- классификацию, особенности конструкции, действия и эксплуатации котельных
установок, поршневых двигателей внутреннего сгорания, газотурбинных и теплосиловых
установок.
Студенты должны уметь:
- производить расчеты требуемых физических величин в соответствии с законами и
уравнениями термодинамики и теплопередачи.
Изучение дисциплины базируется на знании материала дисциплин: «Физика», «Химия»,
«Математика», «Гидравлика», «Инженерная графика», «Метрология, стандартизация и
сертификация».
Настоящие методические указания ставят целью:
 Приобретение практических навыков и умений в выполнении термодинамических
и теплотехнических расчетов;
 Закрепление теоретических знаний по содержанию учебной дисциплины;
 Приобретение навыков творческой самостоятельной деятельности.
Методические указания составлены в соответствии с рабочими программами по
профессиональным модулям для специальностей 21.02.01 и 21.02.02, утвержденными в
Томском политехническом техникуме.
Для выполнения практических заданий в методических указаниях приведены:
 Многовариантные задачи;
 Основные формулы из теории без доказательств;
 Порядок и примеры решения задач.
Для решения предложенных задач требуется предварительное изучение теоретического
материала.
Правила выполнения практических работ
Практические задания следует выполнять в отдельной тетради. Решение каждого
задания следует начинать с новой страницы. Необходимые схемы и графики должны быть
выполнены карандашом, с указанием элементов или величин, входящих в них.
При решении задач необходимо последовательно излагать весь ход расчетов со ссылкой
на соответствующие формулы. Все расчеты производятся в единицах измерений в системе СИ.
Образец заполнения обложки тетради
ТЕТРАДЬ
для практических работ
по термодинамике
студента(ки) 2 курса гр.____
ФИО студента
Практическая работа № 1
РАСЧЁТ ГАЗОВЫХ СМЕСЕЙ
1. Цель работы
Приобретение практических навыков расчета газовых смесей.
2. Требования к отчёту
5.1. Номер работы, тема, цель.
5.2. Записать условие задачи.
5.3. Вычисления начинать с записи расчётных формул в общем виде.
5.4. Размеры величин указывать в системе СИ.
Задание
Природный (или попутный) газ представляет собой смесь, состоящую из метана (СН 4) и
других предельных углеводородов, азота, углекислого газа и сероводорода. Для заданного вида
топлива (см.табл.1.1) определить:
1) Газовую постоянную смеси;
2) Количество подведенного (отведенного) тепла, необходимое для нагрева
(охлаждения) V, м3 смеси от температуры t1, ºС до температуры t2, ºС.
Объемный состав газа указан в табл. П1. Молярные массы элементов определять при
помощи периодической таблицы Менделеева (табл.П2).
№
варта
1
2
3
4
5
6
7
8
9
10
Вид топлива
Природный газ
Попутный газ
Природный газ
Попутный газ
Природный газ
Попутный газ
Природный газ
Попутный газ
Природный газ
Попутный газ
Месторождение
Северо-Ставропольское
Туймазинское
Березовское
Ромашкинское
Уренгойское
Пермское
Медвежье
Бавлинское
Оренбургское
Узеньское
V, м
3
800
1000
1200
1600
1800
2000
2200
2500
1500
900
Таблица 1.1
t1, ºС
t2, ºС
5
65
10
-2
86
13
25
0
74
-10
62
14
88
37
19
70
93
45
22
50
Методические указания
В практической работе №1 необходимо произвести расчет газовой смеси. При решении
следует помнить, что методика расчета смеси зависит от способа задания смеси.
Газовая смесь может задаваться 2-мя способами: 1) через массовые доли компонентов; 2)
через объемные доли компонентов.
Состав природного (попутного) газа задается объемными долями.
Пример: Определить газовую постоянную природного газа Барсуковского
месторождения состава: СО2=0,96%; СН4=80,78%; С2Н6=5,81%; С3Н8=4,8%; С4Н10=4,04%;
С5Н12=1,81%; N2=1,8%. Какое количество тепла нужно подвести к 100 м3 этого газа, чтобы
нагреть его от 20 до 85 ºС? Теплоемкость считать постоянной.
Решение:
Поскольку газовая смесь задана объемными долями, то расчет газовой постоянной смеси
производим по формуле:
𝑅у
𝑅см =
,
𝜇см
Где 𝑅у - универсальная газовая постоянная; 𝑅у =8314 Дж/(кмоль·К); 𝜇см - молярная масса
смеси.
Молярная масса смеси определяется через объемные доли компонентов:
𝜇см = 𝜇1 ∙ 𝑟1 + 𝜇2 ∙ 𝑟2 + ⋯ + 𝜇𝑛 ∙ 𝑟𝑛 ,
Где 𝜇1 , 𝜇2 … 𝜇𝑛 - молярные массы компонентов, а 𝑟1 , 𝑟2 … 𝑟𝑛 - объемные доли
компонентов.
Обозначим: 𝜇1 - молярная масса СО2; 𝜇2 - молярная масса СН4; 𝜇3 - молярная масса
С2Н6; 𝜇4 - молярная масса С3Н8; 𝜇5 - молярная масса С4Н10; 𝜇6 - молярная масса С5Н12 и 𝜇7 молярная масса N2, а 𝑟1 , 𝑟2 … 𝑟7 - их объемные доли соответственно (заданы по условию).
При помощи таблицы Менделеева (табл.П2) находим молярные массы компонентов:
𝜇1 =44 кг/кмоль; 𝜇2 =16 кг/кмоль; 𝜇3 =30 кг/кмоль; 𝜇4 =44 кг/кмоль; 𝜇5 =58 кг/кмоль; 𝜇6 =72
кг/кмоль; 𝜇7 =28 кг/кмоль.
0,96
𝜇см = 𝜇1 ∙ 𝑟1 + 𝜇2 ∙ 𝑟2 + ⋯ + 𝜇7 ∙ 𝑟7 = 44 ∙
+ 16 ∙ 0,8078 + 30 ∙ 0,0581 + 44 ∙ 0,048 +
100
+58 ∙ 0,0404 + 72 ∙ 0,0181 + 28 ∙ 0,018 = 21,35 кг/кмоль.
Газовая постоянная смеси
𝑅у
8314
𝑅см = 𝜇 = 21,35 = 389,4 Дж/(кмоль·К).
см
Для газовой смеси количество подведенного (отведенного) тепла определяется по
формуле
𝑄 = 𝑉 ∙ с′см ∙ ∆Т,
Где 𝑉 - объем газовой смеси, м3; с′см - объемная изохорная теплоемкость смеси,
3
Дж/(м ·К); ∆Т - разность между начальной и конечной температурами.
Объемная теплоемкость смеси рассчитывается по формуле
′
𝑐см
= 𝑐1′ ∙ 𝑟1 + 𝑐2′ ∙ 𝑟2 + ⋯ + 𝑐7′ ∙ 𝑟7 ,
Где 𝑐1′ , 𝑐2′ … 𝑐7′ - объемные теплоемкости компонентов смеси.
Объемные теплоемкости компонентов определим в зависимости от атомности газов.
Молекулярно-кинетическая теория теплоемкости, основанная на допущении о равномерном
распределении энергии по степеням свободы молекул и не учитывающая энергию
внутримолекулярных колебаний, дает следующие значения мольных теплоемкостей:
 для двухатомных газов
cv  20,9 кДж/(кмольК);
 для трех– и многоатомных газов cv  29,3 кДж/(кмольК).
Метан, этан, пропан, бутан, пентан и углекислый газ – трех- и многоатомные газы, поэтому
𝜇𝑐
29,3
𝑐1′ = 𝑐2′ = 𝑐3′ = 𝑐4′ = 𝑐5′ = 𝑐6′ = 22.4𝑣 = 22,4 = 1,308 кДж/(м3·К).
𝜇𝑐
20.9
Азот – двухатомный газ, для него объемная теплоемкость 𝑐7′ = 22.4𝑣 = 22.4 = 0.933 кДж/(м3·К).
′
𝑐см
= 1,308 ∙ (0,808 + 0,0581 + 0,048 + 0,0404 + 0,0181 + 0,0096) + 0,933 ∙ 0,018 = 1,302
кДж/(м3·К).
Рассчитываем количество подведенного тепла по формуле
′
𝑄 = 𝑉 ∙ 𝑐см
∙ ∆𝑇 = 100 ∙ 1,302 ∙ (85 − 20) = 8463 кДж.
Практическая работа № 2
РАСЧЁТ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
1. Цель работы
Приобретение практических навыков расчета основных термодинамических процессов.
2. Требования к отчёту
5.1. Номер работы, тема, цель.
5.2. Записать условия задач.
5.3. Вычисления начинать с записи расчётных формул в общем виде.
5.4. Размеры величин указывать в системе СИ.
5.5. Необходимые схемы, графики и рисунки выполнять карандашом с применением
чертежных принадлежностей.
Задание
Задача 2.1. Изотермически сжимают V м3 газа с Р1= 2,0 кПа до Р2, кПа. Температура газа
t, °С.
Вычислить: 1) параметры газа в начале и конце процесса;
2) работу, затраченную на сжатие;
3) количество тепла, выделенное при сжатии.
4) построить процесс в pV-диаграмме.
Исходные данные взять из табл. 2.1.
Таблица 2.1.
№
вар-та
1
2
3
4
5
6
7
8
9
10
Газ
р2, кПа
t, °С
V, м3
Воздух
Водород
Кислород
Аммиак
Азот
Углекислый газ
Метан
Бутан
Пропан
Сероводород
100
110
120
130
140
150
160
170
180
190
20
30
40
50
60
50
40
30
20
10
150
200
250
300
350
400
450
500
550
600
Задача 2.2. В автоклаве объемом V находится газ под давлением P1 МПа и t1 °С. При
нагревании (V=const) давление в автоклаве поднялось до Р2 МПа.
Определить: 1) сколько тепла сообщено газу в автоклаве;
2) до какой температуры нагреется газ.
3) построить процесс в pV-диаграмме.
Исходные данные взять из табл. 2.2.
Таблица 2.2.
№
вар-та
1
2
газ
V, м3
р1, кПа
t1, °С
р2, кПа
H2S
NH3
0,06
0,05
20
25
10
15
120
130
3
4
5
6
7
8
9
10
CO
CO2
He
Ne
CH4
C2H2
C3H8
N2
0,04
0,03
0,02
0,04
0,06
0,08
0,05
0,1
30
35
40
45
50
55
60
65
25
30
40
50
60
70
80
30
140
155
115
135
165
205
190
180
Задача 2.3. Газ с начальным давлением р1, ат и начальной температурой t1, °С,
расширяется при постоянном давлении от начального объема V1, м3 в n раз.
1) Определить:
- конечные параметры газа;
- работу, затраченную на расширение L;
- тепло, участвующее в процессе Q;
- изменение внутренней энергии ΔU.
2) Построить процесс pV-диаграмме.
Исходные данные взять из табл. 2.3.
№ варта
1
2
3
4
5
6
7
8
9
10
Газ
Воздух
Аргон
Бутан
Пропан
Сероводород
Углекислый газ
Аммиак
Азот
Водород
Кислород
V1, м
n
р1, ат
Таблица 2.3
t1, °С
0,1
0,12
0,14
0,16
0,2
0,23
0,26
0,32
0,41
0,58
2
1,5
1,7
3,0
3,5
2,2
2,4
2,6
1,8
4,0
20
22
24
35
31
28
42
56
33
10
48
24
39
54
18
26
35
44
60
74
3
Задача 2.4. Газ массой m, кг с начальным давлением р1, атм и начальной температурой
Т1, К адиабатно сжимается и объем газа уменьшается в 2 раза.
Определить:
1) Начальные и конечные параметры газа;
2) Количество тепла в процессе;
3) Совершенную работу и изменение внутренней энергии.
4) Изобразить процесс в pV-диаграмме.
Исходные данные взять из табл. 2.4.
Таблица 2.4
№ вар-та Газ
m, кг
р1, атм
Т1, К
1
Воздух
2,5
0,5
288
2
Азот
5,0
0,8
302
3
Водород
3,6
1,1
290
4
Углекислый газ
4,1
0,3
314
5
Сероводород
1,8
0,4
295
6
Метан
2,7
0,6
306
7
Аргон
3,3
1,0
284
8
Гелий
5,6
0,2
310
9
10
Оксид углерода
Аммиак
1,5
7,4
0,7
0,9
325
300
Методические указания
Перед выполнением работы следует внимательно изучить указанные разделы в
литературных источниках.
Необходимо обратить внимание на то, что соотношения между параметрами в
изохорном, изобарном и изотермическом процессе подчиняются законам Шарля, Гей-Люссака
и Бойля-Мариотта соответственно.
В адиабатном процессе все три основных параметра изменяются. Соотношения между
ними описываются следующими уравнениями:
𝑝2
𝑣1
𝑇2
𝑣1
𝑇2
𝑝2 𝑘−1
= ( )𝑘 ;
= ( )𝑘−1 ;
=( ) 𝑘 .
𝑝1
𝑣2
𝑇1
𝑣2
𝑇1
𝑝1
k – показатель адиабаты.
Кроме параметров состояния в практической работе рассчитываются: работа l, кДж/кг;
теплота процесса q, кДж/кг и изменение внутренней энергии Δu, кДж/кг.
Основные формулы расчета процессов приведены в табл.1.
Таблица 1
СоотношеКоличест
График процессов
Наименование между
Формула
во
TS P ние процесса параметраработы L
теплоты
диаграмма диаграмма
ми
Q
Изохорный
процесс
 = const
T1 P1

T2 P2
L=0
Q = U
Q = cT
Изобарный
процесс
P = const
T1 1

T2  2
L = PV
Q= cpT
Изотермический процесс
T = const
Адиабатный
процесс
Pk = const
P11 = P22
P11k
=
P22k
L  mRT ln
L
2
1
mR
(T1  T2 )
k 1
Q=L
Q=0
Q= L+U
Изменение внутренней энергии Δu можно найти из 1-го закона термодинамики
𝑞 = 𝑙 + ∆𝑢,
применительно к соответствующему процессу.
Примеры решения задач
Задача №1. Сернистый газ (SO2) объемом V1=20 м3 сжимают при постоянной
температуре Т=317 К от давления р1=3 кПа до давления р2=300 кПа.
Определить: а) параметры состояния в начале и конце процесса;
б) работу, затраченную на сжатие;
в) количество тепла в процессе;
г) изменение внутренней энергии.
Построить процесс в pV-диаграмме.
Решение:
1) Конечный объем газа находим из соотношения между параметрами в
изотермическом процессе (T=const)
𝑝1 ∙ 𝑣1 = 𝑝2 ∙ 𝑣2 → 𝑉2 =
𝑝1 ∙𝑉1
𝑝2
=
3∙103 ∙20
300∙103
= 0.2 м3.
2) Газовая постоянная SO2
𝑅𝑦
8314
𝑅 = 𝜇 = 64 = 130 Дж/(кг·К).
3) Масса газа
3∙103 ∙20
𝑝 ∙𝑉
1 1
𝑚 = 𝑅∙𝑇
= 130∙317 = 1.46 кг.
4) Работа, затраченная на сжатие
𝑉
0.2
𝐿 = 𝑚 ∙ 𝑅 ∙ 𝑇 ∙ ln(𝑉2 ) = 1.46 ∙ 130 ∙ 317 ∙ ln( 20 ) = −277077.4 Дж.
1
5) Количество тепла в процессе
Т.к. процесс изотермический, изменение внутренней энергии ΔU=0, и по первому зну термодинамики Q=L=-277077.4 Дж.
6) по известным значениям р1, р2, V1 и V2 строим в масштабе процесс в pV-диаграмме.
Задача №2. В баллоне объемом V=0,5 м3 находится кислород (О2) под давлением р1=10 кПа и
температуре t1=17 °С. Газ нагревают при постоянном объеме до давления р2=20 кПа.
Определить: 1) сколько тепла сообщено газу;
2)до какой температуры нагрелся кислород;
3)работу, совершенную газом;
4)изменение внутренней энергии.
Построить процесс в pV-диаграмме.
Решение:
1) Конечная температура газа в изохорном процессе определяется из соотношения
параметров
р1 Т1
р2 ∙ Т1 20 ∙ 103 ∙ (17 + 273)
=
→ Т2 =
=
= 580 К = 307℃.
р2 Т2
р1
10 ∙ 103
2) Газовая постоянная кислорода
𝑅𝑦
8314
𝑅= =
= 260 Дж/(кг·К).
𝜇
32
3) Масса кислорода
𝑚=
𝑝1 ∙𝑉
𝑅∙𝑇1
=
10∙103 ∙0.5
260∙290
= 0.066 кг.
4) Массовая изохорная теплоемкость кислорода определяется через киломольную
теплоемкость с учетом атомности газа.
𝜇𝑐𝑣
𝑐𝑣 =
,
𝜇
Т.к.
кислород
двухатомный
газ
(О2),
то
𝜇𝑐𝑣
20,9
𝑐𝑣 = 𝜇 = 32 = 0,65 кДж/(кг·К).
5) Количество тепла в процессе
𝑄 = 𝑚 ∙ 𝑐𝑣 ∙ (𝑇2 − 𝑇1 ) = 0,066 ∙ 0,65 ∙ (580 − 290) = 12,44 кДж.
6) В изохорном процессе работа сжатия L=0, т.к. объем постоянный. Отсюда по 1-му з-ну
термодинамики ∆𝑈 = 𝑄 = 12.44 кДж.
7) по известным значениям р1, р2, V строим в масштабе процесс в pV-диаграмме.
Задача №3. В цилиндре с поршнем, под постоянным давлением 4 бар, находится воздух
при температуре t1=500 °C. От воздуха отводится тепло таким образом, что в конце процесса
устанавливается температура t2=100 °C. Объем цилиндра, в котором находится воздух, 200 л.
Определить количество отнятого тепла, конечный объем, изменение внутренней энергии
и совершенную над газом работу сжатия.
Решение:
1) выполняем перевод внесистемных единиц измерения в единицы системы СИ: р=4
бар=4·105 Па; V1=200 л=0,2 м3.
2) Конечный объем в изобарном процессе определяем по з-ну Гей-Люссака:
𝑇
(100+273)
𝑉2 = 𝑉1 ∙ 𝑇2 = 0.2 ∙ (500+273) = 0.0966 м3.
1
3) Газовая постоянная воздуха
𝑅𝑦
8314
𝑅 = 𝜇 = 29 = 287 Дж/(кг·К).
4) Масса воздуха
𝑚=
𝑝1 ∙𝑉1
𝑅∙𝑇1
=
4∙105 ∙0.2
287∙773
= 0.361 кг.
5) Массовая изобарная теплоемкость воздуха определяется через киломольную
теплоемкость с учетом атомности газа.
𝜇𝑐𝑝
𝑐𝑝 =
,
𝜇
Т.к.
воздух
двухатомный
газ,
то
𝜇𝑐𝑝
29,3
𝑐𝑝 =
=
=1,01 кДж/(кг·К).
𝜇
29
6) Количество тепла в процессе
𝑄 = 𝑚 ∙ 𝑐р ∙ (𝑇2 − 𝑇1 ) = 0,361 ∙ 1,01 ∙ (373 − 773) = −145,84 кДж.
7) Работа сжатия
𝐿 = 𝑝 ∙ (𝑉2 − 𝑉1 ) = 4 ∙ 105 ∙ (0.0966 − 0.2) = −41360 Дж = −41,36 кДж.
8) Изменение внутренней энергии определим из 1-го з-на термодинамики
∆𝑈 = 𝑄 − 𝐿 = −145.84 + 41.36 = −104.48 кДж.
Задача №4. m=10 кг азота, параметры которого р1=1,2 бар, t1=30 °С, сжимаются, причем
объем уменьшается в 2.5 раза.
Найти начальные и конечные параметры, количество тепла в процессе, работу и
изменение внутренней энергии, если сжатие происходит по адиабате с показателем адиабаты
k=1.4.
Построить процессы сжатия в pV-диаграмме.
Решение:
I.
Расчет адиабатного процесса.
1) Выполняем перевод внесистемных единиц измерения в единицы системы СИ: р=1.2
бар=1,2·105 Па; Т1=30+273=303 К.
2) Газовая постоянная азота
𝑅𝑦
8314
𝑅 = 𝜇 = 28 = 297 Дж/(кг·К).
3) Начальный объем определяем по уравнению состояния
𝑚∙𝑅∙𝑇
10∙297∙303
𝑉1 = 𝑝 1 = 1.2∙105 = 7.5 м3.
1
4) Конечный объем
𝑉2 = 𝑉1⁄2.5 = 7.5⁄2.5 = 3 м3
5) Конечное давление
𝑉
7.5
𝑝2 = 𝑝1 ∙ ( 1 )𝑘 = 1.2 ∙ 105 ∙ ( )1.4 = 4.33 ∙ 105 Па.
𝑉2
3
6) Конечная температура определяется из уравнения состояния для точки 2 окончания
процесса
𝑇2 =
𝑝2 ∙𝑉2
𝑚∙𝑅
=
4.33∙105 ∙3
10∙297
= 434 𝐾.
7) Количество тепла в процессе Q=0, т.к. процесс адиабатный.
8) Работа сжатия
1
1
𝐿 = 𝑘−1 ∙ 𝑅(𝑇1 − 𝑇2 ) = 1.4−1 ∙ 297 ∙ (303 − 434) = −97268 Дж.
9) Изменение внутренней энергии по 1-му з-ну термодинамики
∆𝑈 = −𝐿 = 97268 Дж.
Практическая работа № 3
РАСЧЁТ ЦИКЛА ПОРШНЕВОГО ДВС
1. Цель работы
Приобретение практических навыков расчета цикла поршневого двигателя внутреннего
сгорания.
2. Требования к отчёту
5.1. Номер работы, тема, цель.
5.2. Записать условие задания.
5.3. Вычисления начинать с записи расчётных формул в общем виде.
5.4. Размеры величин указывать в системе СИ.
5.5. Необходимые схемы, графики и рисунки выполнять карандашом с применением
чертежных принадлежностей.
ЗАДАНИЕ
Поршневой двигатель внутреннего сгорания (ДВС) – с изохорно-изобарным подводом
тепла (цикл Тринклера) работает при следующих условиях: начальные давление и температура
р1, t1; степень сжатия ε; степень повышения давления λ; степень предварительного расширения
ρ. Определить параметры состояния р, v, t в характерных точках цикла двигателя, подведенное
и отведенное тепло и термический КПД. Рабочим телом считать воздух, полагая теплоемкость
его постоянной. Масса рабочего тела – 1 кг. Изобразить цикл ДВС в pV-диаграмме.
Исходные данные взять из табл. 3.1.
№
варта
1
2
3
4
5
6
7
р1, кПа
t1, ºС
ε
λ
95
98
96
97
98
100
96
40
30
25
27
17
25
30
16
13
14
15
16
17
18
1,5
1,6
1,5
1,7
1,4
1,5
1,6
Таблица 3.1
ρ
1,5
1,4
1,4
1,3
1,6
1,6
1,3
8
9
10
97
98
99
40
27
17
19
16
18
1,7
1,5
1,6
1,2
1,4
1,3
Методические указания
Перед выполнением работы следует внимательно изучить указанные разделы в
литературных источниках.
При выполнении работы используются уравнения газовых законов, термодинамических
процессов. Кроме этого в условии заданы коэффициенты, характеризующие тип цикла:
𝑣
𝑣
𝑝
𝜀 = 𝑣2 - степень сжатия; 𝜌 = 𝑣4 - степень предварительного расширения; 𝜆 = 𝑝2 - степень
1
3
1
повышения давления.
КПД цикла определяется с учетом количества подведенного и отведенного тепла,
значения которых берутся по абсолютной величине:
𝑞1 − 𝑞2
𝑞2
𝜂𝑡 =
= 1−
𝑞1
𝑞1
Цикл Тринклера.
Рассчитать цикл ДВС: определить параметры в характерных точках цикла, рассчитать
количество подведенного и отведенного тепла и КПД цикла, построить цикл в pV-диаграмме.
Исходные данные: р1=1 МПа; Т1=315 К; λ=2,2; ε=14; ρ=1,9. Рабочее тело – воздух, массой 1 кг.
Решение:
1.Определяем газовую постоянную.
Ry 8314
Дж
R=

 287

29
кг  К
Точка 1
P1V1=RT1
RT
287  315
м3
V1 = 1 

0
,
09
кг
P1
110 6
Точка 2 (линия 1-2 – адиабатный процесс)
T1V1k-1 = T2V2k-1
сp
c p 37,7
кДж
K=
; cp 
;

 1,3
сv
v
29
кг  К
c 29,3
êÄæ
cv  v 
 1,01
.
v
29
êã  Ê
1,3
K=1,01 = 1,3
3
V1
V
0,09
 0,006 м
; V2= 1 =
кг
14
V2

V
0,09 1,3-1
T2 = T1 ( 1 )k-1= 315(
)
=709,8 К
0,006
V2
ε=
P2V2=RT2
RT
287  709,8
 33,9МПа
P2 = 2 
V2
0,006
Точка 3 (линия 2-3 – изохорный процесс)
3
V2 =V3 =0,006 м
кг
P3
λ=
; P3 =λP2 =2,2 ∙ 33,9 =74,58 МПа
P2
PV
74,58  0,006
 1559 К
T3 = 3 3 
R
287
Точка 4 (линия 3-4 – изобарный процесс)
𝑣4
м3
𝜌=
→ 𝑣4 = 𝜌 ∙ 𝑣3 = 1.9 ∙ 0.006 = 0.0114 .
𝑣3
кг
T3 V3
TV
1559  0,0114
; T4  3 4 

 2962,1K
T4 V4
V3
0,006
P3=P4=74,58Мпа
Точка 5 (линия 4-5 – адиабатное расширение)
T4V4k-1 = T5V5k-1
k 1
TV
2962,1  0,0114 0,3 2962,1  0,206
T5  4 k41 

 1258К
0,485
V5
0,09 0,3
Т.к. линия 5-1 – изохорный отвод тепла, то 𝑣5 = 𝑣1 .
P5V5=RT5
𝑅 ∙ 𝑇5 287 ∙ 1258
𝑝5 =
=
= 4.01 МПа.
𝑣5
0.09
Подведенное тепло 𝑞1 = 𝑞1′ + 𝑞1′′ .
кДж
.
кг
кДж
𝑞1′′ = 𝑐𝑝 ∙ (𝑇4 − 𝑇3 ) = 1,3 ∙ (2962,1 − 1559) = 1824,03
.
кг
кДж
𝑞1 = 857,69 + 1824,03 = 2681,72
.
кг
кДж
Отведенное тепло 𝑞2 = 𝑐𝑣 ∙ (𝑇1 − 𝑇5 ) = 1.01 ∙ (315 − 1258) = −952.43 кг .
Определяем КПД
𝑞2
952.43
𝜂𝑡 = 1 − = 1 −
= 0.645.
𝑞1
2681.72
По рассчитанным значениям параметров строится цикл в pV-диаграмме.
𝑞1′ = 𝑐𝑣 ∙ (𝑇3 − 𝑇2 ) = 1,01 ∙ (1559 − 709,8) = 857,69
Практическая работа № 4
РАСЧЁТ ТЕПЛОПЕРЕДАЧИ ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ
1. Цель работы
Приобретение практических навыков расчета процессов теплообмена.
2. Требования к отчёту
5.1. Номер работы, тема, цель.
5.2. Записать условие задания.
5.3. Вычисления начинать с записи расчётных формул в общем виде.
5.4. Размеры величин указывать в системе СИ.
5.5. Необходимые схемы, графики и рисунки выполнять карандашом с применением
чертежных принадлежностей.
ЗАДАНИЕ
Плоская стальная стенка, толщиной δс омывается с одной стороны горячими газами с
температурой t1, а с другой стороны водой с температурой t2. Определить коэффициент
теплопередачи от газов к воде, плотность теплового потока и температуру обеих поверхностей
стенки, если известны коэффициенты теплоотдачи от газа к стенке α1 и от стенке к воде α2.
Определить также все указанные выше величины для случая, если стенка, омываемая водой,
покроется слоем накипи толщиной δн. Для указанных вариантов задачи построить эпюры
температур от t1 до t2. Объяснить, в чем состоит вред отложения накипи на стальных
поверхностях нагрева.
Исходные данные для решения взять из табл. 4.1.
Принять: коэффициент теплопроводности стали λс=50 Вт/(м·К), коэффициент
теплопроводности накипи λн=1 Вт/(м·К).
Таблица 4.1
№
варта
1
2
3
4
5
6
7
8
9
10
δс, мм
δн, мм
α1,
Вт/(м2·К)
α2,
Вт/(м2·К)
t1, °С
t2, °С
14
16
18
20
22
15
17
19
21
23
0,7
0,9
0,8
1,2
1,4
1,0
1,6
1,8
1,7
1,3
32
35
38
40
42
45
34
37
41
44
3200
3600
3000
4000
4300
4600
4200
4500
4300
5000
750
700
780
800
820
850
880
760
830
900
110
120
100
130
150
140
170
160
180
190
Методические указания
Перед выполнением работы следует внимательно изучить указанные разделы в
литературных источниках.
Для выполнения работы следует:
 Знать и различать виды теплообмена;

Знать основные уравнения и расчетные формулы видов теплообмена.
При расчете теплопередачи через плоскую стенку используют следующие формулы:
I)
Для однослойной плоской стенки
Коэффициент теплопередачи К, Вт/(м2·К)
1
𝐾=
.
1 𝛿 1
(𝛼 + + 𝛼 )
𝜆
1
2
2
Удельный тепловой поток q, Вт/м
(𝑡1 − 𝑡2 )
𝑞=
.
1 𝛿 1
(𝛼 + + 𝛼 )
𝜆
1
2
Температуры поверхностей стенок, °С
𝑡𝑤1 = 𝑡1 − 𝑞 ⁄𝛼1 ;
𝑡𝑤2 = 𝑡2 + 𝑞 ⁄𝛼2 .
Где 𝛼1 , 𝛼2 - коэффициенты теплоотдачи от первой жидкости к стенке и от стенки ко
второй жидкости соответственно, Вт/(м2·°С); 𝛿 - толщина стенки, м; 𝜆 - коэффициент
теплопроводности материала стенки, Вт/(м·°С); 𝑡1 , 𝑡2 - температуры первой и второй
жидкости соответственно, °С (см.рис…).
II)
Для многослойной плоской стенки
Коэффициент теплопередачи К, Вт/(м2·К)
1
𝐾=
.
1
1
𝑛 𝛿𝑖
∑
(𝛼 + 𝑖=1 + 𝛼 )
𝜆𝑖
1
2
2
Удельный тепловой поток q, Вт/м
(𝑡1 − 𝑡2 )
𝑞=
.
1
𝛿
1
(𝛼 + ∑𝑛𝑖=1 𝑖 + 𝛼 )
𝜆𝑖
1
2
Температуры поверхностей стенок, °С
𝑡𝑤1 = 𝑡1 − 𝑞 ⁄𝛼1 ;
𝑡𝑤2 = 𝑡1 − 𝑞 ∙ (1⁄𝛼1 + 𝛿1 ⁄𝜆1 );
𝑡𝑤3 = 𝑡2 + 𝑞 ⁄𝛼2 .
Пример решения задачи
Задача. Поверхность нагрева состоит из плоской стальной стенки толщиной Sст = 8 мм. По
одну сторону стенки движется горячая вода, температура которой t1 = 120° С, по другую —
вода с температурой t2 = 60° С. Определить: плотность теплового потока, коэффициент
теплопередачи, значения температур на обеих поверхностях стенки.
Найти, как изменяется плотность теплового потока и температура на поверхности стенки,
если со стороны наибольшего нагрева стальной стенки появится накипь толщиной 1 мм.
Принять: α1=2 000 Вт/(м2 •ºС), α2 = 1250 Вт/(м2 •ºС), λст = 40 Вт/(м •ºС), для накипи λн=
0,5 Вm/(м • ºС).
Решение:
А)без накипи
1) Коэффициент теплопередачи
1
1
Вт
𝐾=
=
= 666 2
.
1
0,008
1
1 𝑆ст 1
м ∙℃
+
+
+
+
40
𝛼1 𝜆ст 𝛼2 2000
1250
2) Плотность теплового потока
𝑞 = 𝐾 ∙ (𝑡1 − 𝑡2 ) = 666 ∙ (120 − 60) = 39960 Вт/м2.
3) Температуры на поверхностях стенки
1
1
= 120 − 39960 ∙
= 100.02 ℃.
𝛼1
2000
1
1
′′
𝑡ст
= 𝑡2 + 𝑞 ∙
= 60 + 39960 ∙
= 91.97 ℃.
𝛼2
1250
′
𝑡ст
= 𝑡1 − 𝑞 ∙
Б) с накипью
1) Коэффициент теплопередачи
1
1
Вт
𝐾=
=
= 285,7 2
.
1
0,001 0,008
1
1 𝑆н 𝑆ст 1
м ∙℃
+
+
+
+
+
+
40
𝛼1 𝜆н 𝜆ст 𝛼2 2000
0,5
1250
2) Плотность теплового потока
𝑞 = 𝐾 ∙ (𝑡1 − 𝑡2 ) = 285,7 ∙ (120 − 60) = 17142 Вт/м2.
3) Температуры на поверхностях стенки
1 𝑆н
1
0.001
′
𝑡ст
= 𝑡1 − 𝑞 ∙ ( + ) = 120 − 17142 ∙ (
+
) = 77.15 ℃.
𝛼1 𝜆н
2000
0.5
1
1
′′
𝑡ст
= 𝑡2 + 𝑞 ∙
= 60 + 17142 ∙
= 73.71 ℃.
𝛼2
1250