Геометрия 8класс
реклама

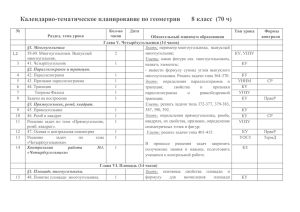
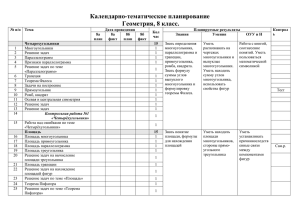
Пояснительная записка Данная рабочая программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов: Федеральный базисный учебный план для ОУ, реализующих программы общего образования (приказ Минобразования России от 09.03.2004 №1312) Программы общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7-9 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2009. – с. 19-21); Федеральный перечень учебников, рекомендованных к использованию в образовательном процессе в ОУ, реализующих программы общего образования на 2014-2015 учебный год; Учебный план МБОУ «Ныргындинская СОШ» на 2014-2015 учебный год. Положение о Рабочей программе учителя, утвержденной приказом директора школы. Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. На изучение предмета отводится 2 часа в неделю, итого 68 часов за учебный год, В том числе: контрольных работ – 5 Изучение геометрии на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования; интеллектуальное развитие, формирование свойственных математической деятельности качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; формирование представлений об идеях и методах геометрии как универсального языка науки и техники, средства моделирования явлений и процессов; воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии. Задачи обучения: Рассмотреть фигуру – четырёхугольник – с различных позиций (виды четырёхугольников, выделить элементы в четырёхугольниках, вывод формул для вычисления площади параллелограмма, квадрата, прямоугольника, ромба, трапеции). Выявить соотношение между гипотенузой и катетами прямоугольного треугольника – теорема Пифагора, а также соотношение между сторонами углами прямоугольного треугольника. Сформировать понятие – подобные треугольники. Научить применять подобие, а также признаки подобия треугольников при доказательстве других теорем и решении задач. Использовать геометрические инструменты для решения задач на построение. Научить проводить анализ геометрических задач на построение. Сформировать понятие окружности и её элементов – касательной, центрального и вписанного углов. Рассмотреть виды окружности – вписанная и описанная. Выделить основные методы доказательств, с целью обоснования (опровержения) утверждений и для решения ряда геометрических задач. Научить проводить рассуждения, используя математический язык, ссылаясь на соответствующие геометрические утверждения. Использовать алгебраический аппарат для решения геометрических задач. Требования к уровню подготовки учащихся. В результате изучения курса ученик должен знать/понимать основные понятия и определения геометрических фигур по программе; формулировки аксиом планиметрии, основных теорем и их следствий; Уметь пользоваться геометрическим языком для описания предметов окружающего мира; распознавать геометрические фигуры, различать их взаимное расположение; изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур; решать задачи на вычисление геометрических величин, применяя изученные свойства фигур и формулы. решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат; проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования; решать простейшие планиметрические задачи в пространстве; владеть алгоритмами решения основных задач на построение. использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: описания реальных ситуаций на языке геометрии; расчетов, включающих простейшие тригонометрические формулы; решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства); построений геометрическими инструментами (линейка, угольник, циркуль, транспортир); владения практическими навыками использования геометрических инструментов для изображения фигур, а также нахождения длин отрезков и величин углов. В результате изучения данного курса учащиеся 8 класса должны уметь/знать: Объяснить, какая фигура называется многоугольником, назвать его элементы. Знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу суммы углов выпуклого многоугольника. Знать определения параллелограмм и трапеции, формулировки свойств и признаков параллелограмма и равнобедренной трапеции; уметь их доказывать и применять при решении задач; делить отрезок на n равных частей с помощью циркуля и линейки и решать задачи на построение. Знать определения прямоугольника, ромба, квадрата, формулировки их свойств и признаков; уметь доказывать изученные теоремы и применять их при решении задач; знать определения симметричных точек и фигур относительно прямой и точки; уметь строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией. Знать основные свойства площадей и формулу для вычисления площади прямоугольника, уметь вывести эту формулу и использовать её и свойства площадей при решении задач. Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу, и уметь применять изученные формулы при решении задач. Знать теорему Пифагора и обратную её теорему; уметь их доказывать и применять при решении задач. Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении площадей подобных треугольников и свойство биссектрисы треугольника; уметь применять их при решении задач. Знать признаки подобия треугольников, уметь их доказывать и применять при решении задач. Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике; уметь их доказывать и применять при решении задач, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение. Знать определения синуса, косинуса, тангенса острого угла прямоугольного треугольника; уметь доказывать основное тригонометрическое тождество; знать значения синуса, косинуса, тангенса для углов 30º, 45º, 60º. Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной; уметь их доказывать и применять при решении задач. Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из ней и теорему о произведении отрезков пересекающихся хорд; уметь доказывать эти теоремы и применять их при решении задач. Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, теорему о пересечении высот треугольника; уметь их доказывать и применять при решении задач. Знать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырёхугольников; уметь их доказывать и применять при решении задач. Учебно-тематический план № параграфа учебника Тема Количество часов Глава 5. Четырёхугольники (14 часов) 1 Многоугольники 2 2 Параллелограмм и трапеция 6 3 Прямоугольник. Ромб. Квадрат. 5 Контрольная работа №1 по теме: «Четырёхугольники» 1 Глава 6. Площадь (14 часов) 1 Площадь многоугольника 2 2 Площадь параллелограмма, треугольника и трапеции 6 3 Теорема Пифагора 5 Контрольная работа №2 по теме: «Площадь» 1 Глава 7. Подобные треугольники (20часов) 1 Определение подобных треугольников 3 2 Признаки подобия треугольников 5 Контрольная работа №3 по теме: «Подобные треугольники» 1 3 Применение подобия к доказательству теорем и решению задач 7 4 Соотношения между сторонами и углами прямоугольного треугольника 3 Контрольная работа №4 по теме: «Применение подобия треугольников» 1 Глава 8. Окружность (16 часов) 1 Касательная к окружности 3 2 Центральные и вписанные углы 4 3 Четыре замечательные точки треугольника 3 4 Вписанная и описанная окружности 5 Контрольная работа №5 по теме: «Окружность» 1 Повторение. Решение задач (2 часа) ИТОГО 68 часов Тематическое планирование № урок а Тема урока 1 Повторение. Решение задач 2 Повторение. Решение задач Содержание урока Четырёхугольники (14 часов) 3 Многоугольники Многоугольники, выпуклые многоугольники, 4 Многоугольники Многоугольник, периметр многоугольника, выпуклый многоугольник, четырёхугольник. Сумма углов выпуклого многоугольника. 5 Параллелограмм Параллелограмм. Свойства параллелограмма 6 Признаки параллелограмма Параллелограмм, его свойства и признаки. 7 Решение задач по теме: «Параллелограмм» Свойства и признаки параллелограмма 8 Трапеция Трапеция, равнобедренная трапеция, свойства равнобедренной трапеции, средняя линия трапеции. 9 Теорема Фалеса Теорема Фалеса. Применение данной теоремы при решении задач. 10 Задачи на построение Задачи на построение. Деление отрезка на п равных частей 11 Прямоугольник Прямоугольник, квадрат, ромб, их свойства 12 Ромб. Квадрат и признаки 13 Решение задач по теме: «Прямоугольник. Ромб. Квадрат» Ромб, квадрат, свойства и признаки ромба и квадрата 14 Осевая и центральная симметрия Осевая и центральная симметрия, практическое применение. 15 Решение задач 16 Контрольная работа №1 по теме: «Четырёхугольники» Определение многоугольника, выпуклого многоугольника, четырёхугольника, параллелограмма, прямоугольника, ромба, квадрата, осевой и центральной симметрии, свойства параллелограмма и его признаки, свойства и признаки ромба, квадрата, прямоугольника. Площадь – 14 часов 17 Площадь прямоугольника Вывод формулы для вычисления площади 18 Площадь прямоугольника 19 Площадь параллелограмма Площадь параллелограмма. Вывод формулы. 20 Площадь треугольника 21 Площадь треугольника Площадь треугольника. Теорема об отношении площадей треугольников, имеющих по равному углу 22 Площадь трапеции Площадь трапеции 23 Решение задач на нахождение площадей фигур Совершенствовать теоретический материал при решении задач 24 Решение задач на нахождение площадей фигур 25 Теорема Пифагора Теорема Пифагора. Пифагоровы тройки 26 Теорема, обратная теореме Пифагора Теорема Пифагора и обратная теорема 27 Решение задач по теме: «Теореме Пифагора» 28 Решение задач 29 Решение задач 30 Контрольная работа №2 по теме: «Площадь» Вывод формулы Герона, решение задач Понятие площади многоугольника, формулы для вычисления площади прямоугольника, параллелограмма, треугольника, ромба, трапеции; теорему Пифагора. Подобие треугольников – 20 часов 31 Определение подобных треугольников Пропорциональные отрезки Подобие треугольников. 32 Отношение площадей Пропорциональные отрезки. Определение подобных треугольников подобных треугольников. Отношение площадей подобных треугольников. Коэффициент подобия. 33 Первый признак подобия Признаки подобия треугольников треугольников 34 Решение задач на применение первого признака подобия треугольников 35 Второй и третий признаки подобия треугольников 36 Решение задач на применение признаков подобия треугольников Признаки подобия треугольников. Применение подобия 37 Решение задач 38 Контрольная работа №3 по теме: «Признаки подобия треугольников» Пропорциональные отрезки. Определение подобных треугольников. Отношение площадей подобных треугольников. Признаки подобия треугольников. Применение подобия 39 Средняя линия треугольника Средняя линия треугольника. Теорема о средней линии треугольника 40 Свойство медиан треугольника 41 Пропорциональные отрезки 42 Пропорциональные отрезки в прямоугольном треугольнике Пропорциональные отрезки в прямоугольном треугольнике Теоремы о точке пересечения медиан треугольника. Применение теории о подобных треугольниках при измерительных работах на местности. 43 Измерительные работы на местности 44 Задачи на построение методом подобия 45 Задачи на построение методом подобия 46 Синус, косинус и тангенс острого угла прямоугольного треугольника Синус, косинус и тангенс острого угла прямоугольного треугольника и у4глов от 0° до 180°. Решение задач. 47 Значение синуса, косинуса, тангенса для углов, равных 30°, 45° и Значения синуса, косинуса, тангенса углов 30°, 45° и 60, метрические соотношения, Практические приложения подобия треугольников . Подобие произвольных фигур 60° приведение к острому углу. 48 Соотношения между сторонами и углами в треугольнике Решение прямоугольных треугольников. 49 Решение задач Алгоритм решения задач на применение теории подобия треугольников и соотношений между сторонами. 50 Контрольная работа №4 по теме: «Соотношения между сторонами и углами в треугольнике» Понятие подобных треугольников; признаки подобия треугольников; синус, косинус, тангенс острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Окружность – 16 часов 51 Взаимное расположение прямой и окружности Взаимное расположение прямой и окружности, двух окружностей. 52 Касательная к окружности 53 Касательная к окружности Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. Касательная, свойство и признак касательной. 54 Градусная мера дуги окружности Дуга, полуокружность, градусная мера дуги окружности, центральный вписанный угол 55 Теорема о вписанном угле Вписанный угол, теорема о величине вписанного угла 56 Теорема об отрезках пересекающихся хорд Теорема об отрезках пересекающихся хорд, ее применение при решении задач. 57 Решение задач по теме «Центральные и вписанные углы» Систематизация теоретических знаний по теме. Решение задач. Метрические соотношения в окружности: свойства секущих, касательных, хорд. 58 Свойство биссектрисы угла Свойства биссектрисы угла и серединного перпендикуляра. Точки пересечения серединных перпендикуляров. биссектрис, медиан. 59 Серединный перпендикуляр . 60 Теорема о точке пересечения высот треугольника Теорема о пересечении высот треугольника, замечательные точки треугольника 61 Вписанная окружность 62 Свойство описанного четырёхугольника Вписанная окружность, описанный многоугольник, теорема о вписанной окружности 63 Описанная окружность 64 Свойство вписанного четырёхугольника 65 Решение задач 66 Контрольная работа №5 по теме: «Окружность» 67 Четырёхугольники. Площади. Повторение 68 Подобные треугольники. Приведение в систему знаний, умений и Окружность. Повтор. навыков учащихся по теме описанная окружность, вписанный многоугольник, теорема об описанной окружности, теорема о сумме противоположных углов вписанного многоугольника касательная к окружности, центральный угол, вписанный угол, замечательные точки треугольника, вписанная и описанная окружность Взаимное расположение прямой и окружности; касательная к окружности, её свойство и признак; центральные и вписанные углы; четыре замечательные точки треугольника; вписанная и описанная окружности. Приведение в систему знаний, умений и навыков учащихся по теме Материально-техническое обеспечение Геометрия 7-9, Атанасян Л.С. и др. М.: Просвещение,2013г. Зив Б.Г. .Геометрия: дидактические материалы для 8 кл. / Б. Г. Зив, В.М. Мейлер. — М.: Просвещение, 2007—2010. Электронное приложение к учебникуЛ.С.Атанасяна, С.Б.Кадомцева Изучение геометрии в 8 классе: методические рекомендации: кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. -М.: Просвещение, 2010г. Рабочие программы по геометрии:8 класс /Составитель Г.И.МаслаковаМ.:ВАКО, 2014г. Зив Б.Г. .Геометрия: дидактические материалы для кл. / Б. Г. Зив, В.М. Мейлер. — М.: Просвещение, 2010.