Задача № 1. Дано: Решение: = 28кH; F

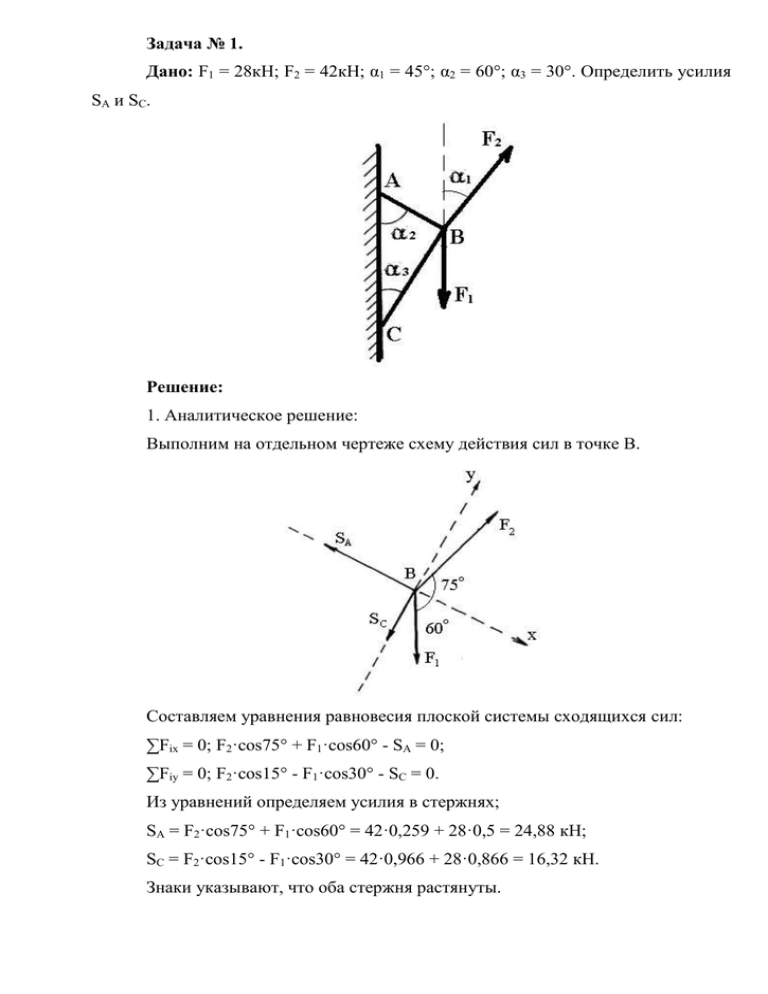
Задача № 1.
Дано: F1 = 28кH; F2 = 42кH; α1 = 45°; α2 = 60°; α3 = 30°. Определить усилия
SA и SС.
Решение:
1. Аналитическое решение:
Выполним на отдельном чертеже схему действия сил в точке В.
Составляем уравнения равновесия плоской системы сходящихся сил:
∑Fix = 0; F2·cos75° + F1·cos60° - SА = 0;
∑Fiу = 0; F2·cos15° - F1·cos30° - SС = 0.
Из уравнений определяем усилия в стержнях;
SА = F2·cos75° + F1·cos60° = 42·0,259 + 28·0,5 = 24,88 кН;
SС = F2·cos15° - F1·cos30° = 42·0,966 + 28·0,866 = 16,32 кН.
Знаки указывают, что оба стержня растянуты.
2. Графическое решение
Выбираем масштаб сил m = 10 кН/см, тогда силы F1 и F2 будут откладываться отрезками
F1 28
=
= 2,8 см;
m 10
F2 42
=
=
= 4,2 см.
m 10
F1m =
F2m
Строим силовой многоугольник.
Измеряя отрезки SAm и SCm и, умножая их на масштаб, находим значение
SA и SC:
SA = SAm·m = 2,5·10 = 25 кН;
SС = SСm·m = 1,62·10 = 16,2 кН.
Вычислим допущенную при графическом решении ошибку:
𝛿А =
𝛿С =
25 − 24,88
∙ 100 % = 0,48 %;
24,88
16,32 − 16,2
∙ 100 % = 0,73 %.
16,32
Ошибка находится в разрешённых пределах (менее 2 %).
Задача № 2.
Дано: F = 24 кH; q = 6 кН/м; М = 12 кН·м α = 60°; а = 1,8 м; b = 5,2 м; с =
3,0 м. Определить реакции VA, HA и VВ.
Решение:
Определяем равнодействующую распределенной нагрузки:
Q = q·a2 = 6·5,2 = 31,2 кН.
Для полученной произвольной плоской системы сил составляем уравнения
равновесия:
∑Fix = 0; HA – F·cos60° = 0;
∑Fiу = 0; VA – F·cos30° – Q + VB = 0;
∑МА(Fi) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – М – VB·(1,8 + 5,2 + 3) = 0.
Решаем систему уравнений.
HA = F·cos60° = 24·0,5 = 12 кН;
VB =
Q ∙ (1,8 + 2,6) + F ∙ cos30° ∙ (1,8 + 5,2) − М
;
1,8 + 5,2 + 3
31,2 ∙ 4,4 + 24 ∙ 0,866 ∙ 7 − 12
= 27,08 кН;
10
VA = F·cos30° + Q – VB = 24·0,866 + 31,2 – 27,08 = 24,9 кН.
VB =
Проверка:
∑МА(Fi) = VA·7 – Q·2,6 – М – VB·3 = 24,9·7 – 31,2·2,6 – 12 – 27,08·3 = – 0,06.
Задача № 3.
Дано: F1 = 28кН; F2 = 64кН; l1 = 2,4м; l2 = 2,2м; l3 = 2,0м; А = 3,2см2;
Е = 2,1∙105 МПа.
Решение:
Проводим ось z
В
сторону свободного конца бруса и определяем реакцию
заделки
∑FRZ = F1 – F2 + V = 0;
V = – F1 + F2 = – 28 + 64 = 36 кН.
Определяем величины продольных сил:
N1 = F1 = 28 кН.
N2 = F1 = 28 кН;
N3 = F1 – F2 = 28 – 64 = -36 кН.
По найденным значениям продольной силы строим соответствующую
эпюру. Определяем нормальные напряжения в характерных сечениях бруса по
формуле:
σ=
N
;
A
N1 28 ∙ 103
σ1 =
=
= 87,5 Н⁄мм2 = 87,5 МПа;
A1 3,2 ∙ 102
N2 28 ∙ 103
σ2 =
=
= 43,75 МПа;
A2 6,4 ∙ 102
N3 −36 ∙ 103
σ3 =
=
= −112,5 МПа.
A1
3,2 ∙ 102
Строим соответствующую найденным значениям эпюру.
Определяем абсолютное удлинение бруса:
∆l = σ1
l1
l2
l3
+ σ2 + σ3 .
E
E
E
103
∆l =
∙ (87,5 ∙ 2,4 + 43,75 ∙ 2,2 − 112,5 ∙ 2,0) = 0,39 мм.
2,1 ∙ 105
Задача № 4.
Дано: Р1 = 30 кВт; Р2 = 10 кВт; Р3 = 12 кВт; Р4 = 8 кВт; l1 = 0,4 м; l2 = 0,3 м;
l3 = 0,5 м; ω = 100 рад/с.
Решение.
Мощность, подводимая к валу без учёта потерь на трение, равна сумме
мощностей, снимаемых с вала:
Р1 = Р2 + Р3 + Р4 = 10 + 12 + 8 = 30 кВт.
Определяем вращающий момент на шкивах по формуле:
m
P
;

30 10 3
10  10 3
m1 
 300 Н  м; m 2 
 100 Н  м;
100
100
12  10 3
8  10 3
m3 
 120 Н  м; m 4 
 80Н  м.
100
100
При равновесии момент движущий равен сумме моментов сопротивления:
m1 = m2 + m3 + m4 = 100 + 120 + 80 =300.
Определяем крутящие моменты в поперечных сечениях бруса с помощью
метода сечений.
Мк1 = – m4 = – 80 Н∙м;
Мк2 = – m4 – m3 = – 80 – 120 = – 200 Н∙м;
Мк3 = – m4 – m3 + m1 = – 80 – 120 + 300 = 100 Н∙м;
Мк4 = – m4 – m3 + m1 – m2 = – 80 – 120 + 300 – 100 = 0 Н∙м.
По полученным значениям строим эпюру крутящих моментов.
Исходя из условия прочности:
τmax =
Mk max
≤ [τ],
Wх
где Мк max – максимальный крутящий момент на валу; Мк max = 200 Н·м;
Wρ – осевой момент сопротивления круглого сечения;
π ∙ d3
Wх =
≈ 0,2d3 .
16
Таким образом
200
0,2d 3
≤30 МПа ;
Диаметр вала:
d
=3
200 • 10 3
= 32,18 мм.
0,2 • 30
Определяем углы закручивания на каждом участке вала:
φ=
180° Мк ∙ l
∙
,
π Jρ ∙ G
где G – модуль упругости сдвига; G = 8·104 МПа.
Jρ – полярный момент инерции; для круга равен
π ∙ d4
Jρ =
≈ 0,1d4 .
32
180° 80 ∙ 103 ∙ 0,4 ∙ 103
φ1 =
∙
= 0,21°;
3,14 0,1 ∙ 32,184 ∙ 8 ∙ 104
180° 200 ∙ 103 ∙ 0,3 ∙ 103
φ2 =
∙
= 0,4°;
3,14 0,1 ∙ 32,184 ∙ 8 ∙ 104
180° 100 ∙ 103 ∙ 0,5 ∙ 103
φ3 =
∙
= 0,33°;
3,14 0,1 ∙ 32,184 ∙ 8 ∙ 104
Задача № 5.
Дано: Fl = 24 кН; F2 = 36 кН; a = 2 м; b = 3 м; c = 3 м; М1 = 18 кН∙м; М2 = 24
кН∙м; [σ] = 160 МПа.
Решение:
Составляем уравнения равновесия параллельной системы сил.
∑МА(Fi) = 0; F1·2 + M1 +F2·3 – M2 – VB·6 = 0;
(1)
∑МВ(Fi) = 0; F1·8 + M1 +F2·3 – M2 – VА·6 = 0;
(2)
Определяем реакции опор:
−F1 ∙ 8 − M1 + F2 ∙ 3 + M2 −24 ∙ 8 − 18 + 36 ∙ 3 + 24
=
= −13 кН.
6
6
F1 ∙ 2 + M1 + F2 ∙ 3 − M2 24 ∙ 2 + 18 + 36 ∙ 3 − 24
VВ =
=
= 25 кН.
6
6
Проверка:
VA =
∑Fiу = F1 –VA – F2 + VB = 24 – 13 – 36 + 25 = 0.
Реакции определены верно.
Определяем значения поперечной силы Q в характерных сечениях балки.
Q1 = Q2лев = F1 = 24 кН;
Q2прав = Q3лев = F1 –VA = 24 – 13 = 11 кН;
Q3прав = Q4лев = F1 –VA – F2 = 24 – 13 – 36 = – 25 кН.
По найденным значениям строим эпюру поперечных сил Q. Определяем
значения изгибающего момента МИ в характерных сечениях балки:
МИ1 =0;
МИ2лев = F1·2 = 24·2 = 48 кН·м;
МИ2прав = М2лев + М1 = 48 + 18 = 66 кН·м;
МИ3 = F1·5 + М1 – VA·3 = 24·5 + 18 – 39 = 99 кН·м;
МИ4 = М2 = 24 кН·м.
По найденным значениям строим опору изгибающих моментов МИ.
По эпюре изгибающих моментов определяем положение опасного сечения
балки (сечения, в котором изгибающий момент имеет наибольшее значение по
абсолютной величине). В нашем случае Мmax = 99 кН·м.
Из условия прочности балки на изгиб
σ=
Мmax
≤ [σ]
Wx
вычисляем необходимый осевой момент сопротивления:
Mmax 99 ∙ 106
Wx =
=
= 0,619 ∙ 106 мм3 = 619 см3 .
[σ]
160
В соответствии с ГОСТ 8239—89 (таблица 1) принимаем сечение из стального двутавра № 33 с WХ = 597 cм3.
Имеем напряжение:
Мmax
99 ∙ 106
σ=
=
= 165,8 МПа.
Wx
597 ∙ 103
σ=
σmax − [σ]
165.8 − 160
∙ 100 % =
∙ 100 % = 3,6 % < 5 %,
[σ]
160