Лабораторная работа №4. «Изучение излучающей способности
реклама

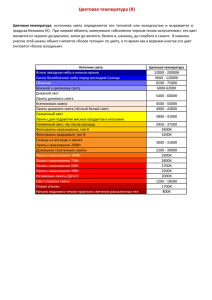
Лабораторная работа №4. «Изучение излучающей способности металла». Цель работы: изучить закон теплового излучения на примере прохождения постоянного электрического тока через вольфрамовую нить накала лампы. Задачи работы: снятие вольт-амперной характеристики вольфрамовой нити лампы накаливания; определение температур вольфрамовой нити лампы накаливания в рабочем режиме; исследование излучающей способности вольфрамовой нити лампы накаливания от температуры. Оборудование: лампа накаливания (3,5 В; 0,26 А), миллиамперметр, вольтметр, источник постоянного тока, реостат, ключ, соединительные провода – лабораторный набор «Lmicro». Теория и метод выполнения работы: Тепловое излучение – испускание электромагнитных волн за счет внутренней энергии тела (энергии теплового движения атомов и молекул вещества). Оно происходит при любой температуре тела и имеет сплошной спектр, положение максимума которого зависит от температуры тела (вещества). При невысоких температурах излучаются лишь электромагнитные волны с большой длиной волны (инфракрасная область спектра). С повышением температуры возрастает общая энергия испускаемого теплового излучения, а положение максимума перемещается в область малых длин волн. Тепловое излучение испускает, например, поверхность накаленного металла, земная атмосфера, кожный покров человека и т.д. Все остальные виды излучения, возбуждаемые за счет любого другого вида энергии, кроме внутренней (например, налетающими частицами, фотонами, механическим воздействием), носят название – люминесценции. Очень важными характеристиками теплового излучения являются энергетическая светимость, спектральная плотность энергетической светимости тела, испускательная и поглощательная способности. Энергетической светимостью тела называется поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π) R W . В 1879 г. Й. Стефан (Йозеф tS Стефан, австрийский физик, 1835–1893), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость R~T4. Стефан считал, что этот закон справедлив для интегральной светимости всех тел. Однако оказалось, что он строго выполняется только для абсолютно черного тела. Это показал в 1884 г. Л. Больцман (Людвиг Больцман, австрийский физик–теоретик, 1844–1906), исходя из законов классической термодинамики и используя результаты теории электромагнетизма 4 Максвелла: R T . Последнее соотношение получило название закона Стефана– Больцмана: энергетическая термодинамической светимость температуры. тел Константу пропорциональна σ называют четвертой степени постоянной Стефана– Больцмана. Ее экспериментальное значение равно: σ = 5,6696∙10–8Вт/м2∙К4. Абсолютно черное тело – обладает свойством поглощать все излучение, что падает на это тело. Абсолютно черных тел не бывает в природе. Наиболее близко к нему приближаются: сажа, платиновая чернь, но и то лишь в некоторой области частот. Для реальных тел вводят понятие серого тела, которое поглощает часть падающей энергии, но одинаковую n для всех частот. Поэтому для нечерного тела выполняется соотношение R const T , где const и n принимают различные значения для разных температурных интервалов. При высоких температурах спирали лампы накаливания потерями тепла за счет теплообмена можно пренебречь, поэтому можно считать, что вся подводимая к лампе мощность расходуется на излучение, т.е. P=R∙S=const∙S∙Tn, где: R – энергетическая светимость, S – площадь поверхности спирали, P=I∙U – подводимая к лампе накаливания мощность, T – абсолютная температура накала лампы, определяется по зависимости сопротивления металлического проводника от его температуры Rt R0 1 t . Для исследования излучающей способности вольфрамовой нити лампы накаливания от температуры обе части выражения I∙U =const∙S∙Tn прологарифмируем: ln(I∙U) =ln(const∙S∙Tn) Используя свойства логарифмов, представим в виде: ln(I∙U) =ln(const∙S)+n∙lnT Если построить графическую зависимость ln(I∙U) =f(lnT), то угловой коэффициент, определяет значение показателя n в законе теплового излучения реального тела R const T n . Аналитическое выражение, описывающее зависимость сопротивления металла от температуры имеет вид: Rt R0 1 t Rt – сопротивление металла при температуре t; R0 – сопротивление металла при 0 0С; температурный коэффициент сопротивления металла; t – изменение температуры в сравнении с 20 0С; Упрощённая формула принимает вид: Rt R0 1 t При вычислении температуры вольфрамовой нити лампы накаливания в рабочем режиме предполагаем: R0 – сопротивление металла при 0 0С совпадает с сопротивлением вольфрамовой нити лампы накаливания неизлучающей свет (1-я пара экспериментальных значений силы тока и напряжения) при комнатной температуре 20 0С; Rt – сопротивление металла при температуре t совпадает с сопротивлением вольфрамовой нити лампы накаливания излучающей свет; при расчёте R0 и Rt использовать закон Ома для участка цепи: Rt R0 1 t U I 1 Ut U0 1 t t t 0 1 200 С It I0 U0 It температурный коэффициент сопротивления вольфрама =0,0048 (С-1) К-1 Таким образом, в данной лабораторной работе исследуется вольт-амперная характеристика лампы накаливания накаливания от электрической I=f(U), зависимость сопротивления лампы мощности R=f(P), подводимой к лампе, зависимость сопротивления лампы накаливания от температуры R=f(T), зависимость подводимой электрической мощности от температуры вольфрамовой нити лампы накаливания P=f(T) и графическая зависимость ln(I∙U) =f(lnT). Ход работы: 1. Используя лабораторное оборудование, собрать экспериментальную установку для снятия вольт-амперной характеристики вольфрамовой нити лампы накаливания по схеме: 2. Установить выходное напряжение на источнике постоянного тока 3÷3,5 В. 3. Плавно изменяя положение ползунка реостата заполнить раздел «Измерено» таблицы экспериментальных данных. 4. Используя закон Ома для участка цепи Rt накаливания и результаты занести в U рассчитать сопротивление лампы I раздел «Вычислено» таблицы экспериментальных данных. 5. Рассчитать электрическую мощность, подводимую к лампе накаливания P=I∙U. Результаты занести в раздел «Вычислено» таблицы экспериментальных данных. 6. По формуле U I 1 t t 0 1 U0 It определить температуру нити лампы накаливания, представить значения температур в термодинамической шкале и результаты занести в раздел «Вычислено» таблицы экспериментальных данных. 7. Определить lnP и lnT. Результаты вычислений занести в раздел «Вычислено» таблицы экспериментальных данных. Таблица экспериментальных данных Измерено I, А U, В Вычислено R, Ом P, Вт t, 0C T, К lnP lnT 8. Построить в Microsoft Excel, используя мастер диаграмм с добавлением линии тренда, указанием уравнения: вольт-амперную характеристику лампы накаливания I=f(U); зависимость сопротивления лампы накаливания от электрической мощности R=f(P), подводимой к лампе; зависимость сопротивления лампы накаливания от температуры R=f(T); зависимость подводимой электрической мощности от температуры вольфрамовой нити лампы накаливания P=f(T), определить по уравнению кривой значение показателя n в законе теплового излучения реального тела R const T n ; графическую зависимость ln(I∙U) =f(lnT), определить по уравнению прямой значение показателя n в законе теплового излучения реального тела R const T n . 9. Сформулировать общий вывод по лабораторной работе.