ЛАБОРАТОРНАЯ РАБОТА №2. Основы анализа эффективности алгоритмов.

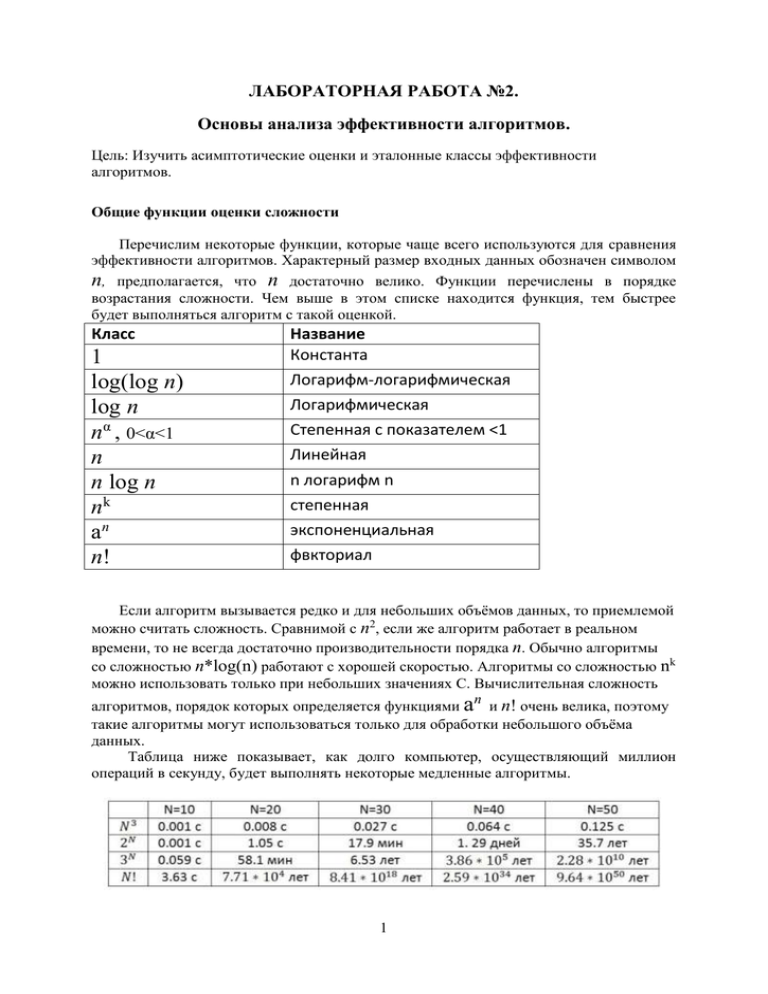
ЛАБОРАТОРНАЯ РАБОТА №2.
Основы анализа эффективности алгоритмов.
Цель: Изучить асимптотические оценки и эталонные классы эффективности
алгоритмов.
Общие функции оценки сложности
Перечислим некоторые функции, которые чаще всего используются для сравнения
эффективности алгоритмов. Характерный размер входных данных обозначен символом
n, предполагается, что n достаточно велико. Функции перечислены в порядке
возрастания сложности. Чем выше в этом списке находится функция, тем быстрее
будет выполняться алгоритм с такой оценкой.
Класс
1
log(log n)
log n
nα , 0<α<1
n
n log n
nk
an
n!
Название
Константа
Логарифм-логарифмическая
Логарифмическая
Степенная с показателем <1
Линейная
n логарифм n
степенная
экспоненциальная
фвкториал
Если алгоритм вызывается редко и для небольших объёмов данных, то приемлемой
можно считать сложность. Сравнимой с n2, если же алгоритм работает в реальном
времени, то не всегда достаточно производительности порядка n. Обычно алгоритмы
со сложностью n*log(n) работают с хорошей скоростью. Алгоритмы со сложностью nk
можно использовать только при небольших значениях C. Вычислительная сложность
n
алгоритмов, порядок которых определяется функциями a и n! очень велика, поэтому
такие алгоритмы могут использоваться только для обработки небольшого объёма
данных.
Таблица ниже показывает, как долго компьютер, осуществляющий миллион
операций в секунду, будет выполнять некоторые медленные алгоритмы.
1
О-, Ω- и Θ-обозначения эффективности
Для указания и сравнения асимптотических порядков роста функций, выражающих
эффективность алгоритмов, используются О- Ω- и Θ – обозначения (О большое, омега
и тэта).
Оценка О большое требует, чтобы функция f(n) не превышала значения функции
g(n) при n>n0 с точностью до положительного постоянного множителя, а именно
f(n)=O(g(n)), если:
O(g(n)) обозначает класс функций, таких, что все они растут не быстрее, чем
функция g(n) с точностью до положительного постоянного множителя. Говорят, что
функция g(n) мажорирует функцию f(n). Например, для всех функций:
f1(n)=12, f2(n)=5n+23, f3(n)=n*ln n, f4(n)=7n2+12n-34
будет справедлива оценка O(n2).
Следует указывать наиболее «близкую» мажорирующую функцию, поскольку,
например, для функции f ( n ) = 12n3 справедлива оценка 0 ( 2 n ) , однако практически
она будет мало пригодна.
Оценка Θ (тета). Говорят, что функция f(n)=Θ(g(n)), если:
Функция g ( n ) является асимптотически точной оценкой функции f ( n ) , т. к.
функция f ( n ) отличается от функции g(n) на положительный ограниченный
множитель при всех значениях аргумента n>n0.
Запись f(n)=Θ(1) означает, что функция f(n) или равна константе, не равной нулю,
или ограничена двумя положительными константами при любых значениях аргумента
n>n0.
Функция Θ(g(n)) есть обозначение класса функций, каждая из которых
удовлетворяет условию выше.
2
Оценка Ω (омега). Оценка Ω является оценкой снизу – т.е. определяет класс
функций, которые растут не медленнее, чем функция g(n) с точностью до
положительного постоянного множителя: f(n)=Ω(g(n)), если:
Например, запись Ω(n*ln n) обозначает класс функций, которые растут не
медленнее, чем g(n) = n*ln n, в этот класс попадают, например, все полиномы со
степенью больше единицы.
1. Задания для выполнения лабораторной работы 2.
Задание 1.
Построить графики функций:
1) log(log n);
2) ln n;
3) sqrt(n);
4) n;
5) n*log n;
6) n3/2;
7) n2;
8) n3;
9) 2(logn);
10) 2n;
11) n!;
3
12) nn;
13) n2+n;
14) (n-1)/(n+3);
15) n3 + 2n2+3;
16) log n2;
17) n3-n2;
18) n4 + 2n+3;
19) log 2n
Задание 2. Определите, к какому классу относятся указанные функции, поставьте в
соответствующую клетку таблицы +.
O(1)
O(n)
O(n2)
O(nlogn)
O(n3)
O(2n)
O(n!)
2log n
22n+1
( n+1)!
ln n
n log log n
Задание 3. Определите, истинны или ложны следующие утверждения?
Задание 4. Для каждой из приведенных функций укажите класс Θ(g(n)), к которому
относится функция. (При ответе используйте максимально простую функцию g(n)).
Задание 5. Расположите перечисленные ниже функции в соответствии с их порядком
роста(от меньшего к большему).
Задание 6.
4
Задание 7. Докажите теорему.
2. Контрольные вопросы к лабораторной работе 2.
1.
2.
3.
4.
Расскажите про общие функции оценки сложности алгоритмов;
Опишите О-обозначения эффективности;
Опишите Ω-обозначения эффективности;
Опишите Θ-обозначения эффективности.
5