Хэш-функции
реклама

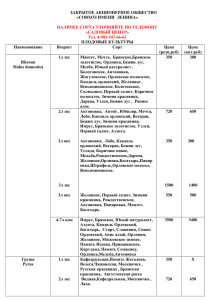
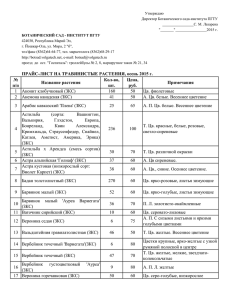
184-190стр.Молдовян Н.А, Молдовян А.А. Введение в криптосистемы с открытым ключом.-СПб.:БХВ-Петербург, 2005.-288с.:ил. Хэш-функции Защита от модифицирования данных Защита информации от модифицирования требует решения комплекса задач, связанных с надежностью аппаратного и программного обеспечения, организационными вопросами, резервированием данных, защитой от компьютерных вирусов, проверкой целостности данных, оперативностью их восстановления и др. В реальных информационных системах всегда имеется существенная вероятность модифицирования информации. Одной из важнейших задач защиты от модифицирования данных является обнаружение факта искажения информации. Во многих случаях обнаружение этого факта является достаточно сложной задачей. Последствия от использования модифицированных программ и данных в информационных автоматизированных системах могут привести к большому экономическому ущербу. Причинами нарушения целостности информации являются ненадежность аппаратных средств, используемых в информационных технологиях, воздействие внешних электромагнитных излучений, наличие естественных помехе каналах связи, ошибки операторов и программистов, компьютерные вирусы и действия нарушителей. Многие из этих причин вызывают появление непреднамеренных ошибок, которые имеют случайный характер, а другие связаны с умышленными воздействиями на информацию. Это может быть осуществлено специально внесенной в компьютерную систему программой или специально разработанным вирусом. Нарушитель, получая возможность несанкционированного доступа к информационным ресурсам, может внести изменения в электронные документы, модифицировать технологическую программу, удалить информацию из базы данных или внести дополнительную информацию. Умышленные воздействия имеют целенаправленный характер. При целенаправленном внесении изменений нарушитель может учитывать используемые механизмы обнаружения модификаций с целью осуществления такого модифицирования, которое нельзя было бы обнаружить. В некоторых ситуациях умышленные воздействия будут приводить к случайному модифицированию данных, например, при модифицировании зашифрованных данных. Очевидно, что если решается задача обнаружения целенаправленного модифицирования, то одновременно решается и задача обнаружения случайных искажений информации. Одним из способов проверки целостности информации является хранение эталонных копий, используемых для сравнения. Однако при необходимости частых проверок целостности данных большого объема такая процедура приводит к существенным временным задержкам, поэтому она применяется только в специальных случаях. Более технологичным является способ, основанный на вычислении по сложным законам некоторых контрольных сумм. Вычисляются контрольные суммы для массивов данных (например файлов, каталогов), находящихся в так называемом эталонном состоянии. Эти эталонные контрольные суммы записываются в таблицы, которые затем используются для проверки целостности информации. В этом случае проверка целостности состоит в вычислении по заданному алгоритму контрольной суммы для данного блока информации и сопоставлении полученного значения с эталонным значением контрольной суммы. Выигрыш состоит в том, что теперь нет необходимости проводить сравнение двух больших массивов данных. Целостность проверяется путем сравнения, например 64битовых, 128-битовых или 256-битовых контрольных сумм. Такие контрольные суммы называются защитными контрольными суммами (ЗКС). Для их вычисления необходимо использовать алгоритмы, которые обеспечивают влияние каждого бита сообщения на значение выходного кода, описываемое некоторым «сложным» законом. Иными словами, требуется алгоритм с хорошими свойствами рассеивания. В связи с этим криптографические преобразования используются не только для закрытия передаваемых или хранимых сообщений, но и для контроля целостности информации. Применяются различные типы алгоритмов вычисления ЗКС в зависимости от конкретных угроз целостности информации и требуемого уровня необнаружения модификаций данных. Двумя основными типами алгоритмов вычисления ЗКС являются: • секретные (или использующие секретный ключ); • открытые (или бесключевые). Первые используют секретный ключ, или сами являются секретными (наиболее удобным является использование секретного ключа). Вторые не содержат никаких секретных элементов и известны потенциальным нарушителям. В зависимости от конкретной решаемой задачи применяются алгоритмы вычисления ЗКС первого или второго типа. Для защиты от непреднамеренных модификаций могут быть применены оба варианта. Для защиты от преднамеренных искажений также могут быть использованы секретные или открытые алгоритмы, однако во втором случае требуется обеспечить целостность самой контрольной суммы, чтобы нарушитель не мог осуществить замену исходного значения ЗКС на новое, вычисленное от модифицированного сообщения. Для этого контрольные суммы могут храниться в зашифрованном виде (т. е. опять приходим к использованию секретного ключа) или на носителях, которые являются недоступными для потенциальных нарушителей. При использовании алгоритмов с хорошими криптографическими свойствами 64-битовые ЗКС являются вполне достаточными для обнаружения умышленного модифицирования информации в случае, когда значение ЗКС недоступно нарушителю (вероятность необнаружения равна 2 64 В случае открытых алгоритмов нарушитель может вычислить эталонное значение ЗКС и попытаться осуществить очень большое число экспериментов с целью получения модифицированного сообщения, значение ЗКС которого равно эталонному. В случае mбитовых ЗКС при количестве таких экспериментов 2 m имеется вероятность более 1/2, что нарушителем будет обнаружено нужное ему модифицированное сообщение. Следовательно, если указанная угроза актуальна и потенциальный нарушитель имеет доступ к большим вычислительным ресурсам, то можно рекомендовать использование значения m 96 . Разновидностью контрольной суммы является имитовставка, которая представляет собой некоторую дополнительную информацию, имеющую сравнительно малый размер и присоединяемую к передаваемому шифртексту. Имитовставка может быть вычислена по следующей итеративной формуле S i Ek ( M i S i 1 ) , где К — секретный ключ (не обязательно совпадающий с ключом, использованным для шифрования сообщения), Л/, - совокупность блоков данных, на которые разбивается сообщение, преобразуемое с помощью некоторой функции шифрования E, i 1,2,..., n. Если используется имитовставка длиной т бит, то вероятность того, что имевшая место модификация данных не будет обнаружена приемной стороной, составляет 2 m .Свойство защищенности криптосистемы от навязывания ложных сообщений называется имитостопкостью, которую можно оценить вероятностью необнаружения искажений криптограммы. Во многих практических случаях значение т - 64 или даже т = 32 обеспечивает приемлемую имитостойкость. Приведенная выше формула фактически описывает шифрование в режиме сцепления блоков шифра, но выходом является не все зашифрованное сообщение, а только последний блок, значение которого и служит контрольной суммой. Криптографические контрольные суммы Важнейшим типом ЗКС являются хэш-функции, относящиеся к бесключевым ЗКС. Хэш-функции иногда называют криптографическими контрольными суммами. В связи с их применением в системах ЭЦП в качестве цифрового «отпечатка пальцев» малого размера (128, 160 или 256 бит) от электронного документа большого размера (например 10 бит) к ним предъявляются наиболее жесткие требования по сравнению с другими типами алгоритмов ЗКС. Вместо подписывания большого числа фрагментов документа вырабатывается подпись к хэшфункции, вычисленной от документа. Это значительно ускоряет процедуру подписывания документа, поскольку алгоритмы хэширования работают очень быстро, но основным достоинством является многократное сокращение длины подписи, что имеет важное практическое значение при работе с большим числом подписанных электронных документов. Хэш-функция должна удовлетворять следующим требованиям: • аргументом для хэш-функции может быть сообщение произвольной длины; • значение хэш-функции имеет фиксированную разрядность (фиксированный размер); • хэш-функция является эффективно вычислимой; • хэш-функция является криптографически стойкой. Эффективная вычислимость означает, что алгоритмы хэшфункций при программной и/или аппаратной реализации должны иметь достаточно высокую производительность. По стойкости к хэш-функциям предъявляются наиболее высокие требования по сравнению с различными вариантами ЗКС. Особые требования к хэш-функциям связаны с тем, что ряд атак на ЭЦП основан на нападениях на используемые хэш-функции. В частности, так называемая атака с помощью секретарши представляет собой попытку сформировать два документа — легальный и модифицированный, имеющие одинаковое значение хэш-функции. После подписывания хэш-функции проверяющему направляется модифицированный документ, который успешно пройдет процедуру проверки подписи, так как полученное от него значение хэш-функции на самом деле подписано владельцем секретного ключа, хотя последний полагал, что подписывал легальный документ. Потенциальная возможность осуществления такой атаки диктует наиболее жесткое требование к хэш-функциям, которое формулируется следующим образом: хэш-фулщия должна быть стойкой к коллизиям. Это означает, что нахождение двух сообщений (документов), имеющих одно и то же значение хэшфункции, является вычислительно сложной задачей, которая не может быть решена за обозримое время. При этом предполагается, что атакующий может использовать очень большие вычислительные ресурсы, например организовать атаку с использованием миллионов процессоров и памяти порядка 1016 байт. Пусть Н есть хэш-функция, а М — сообщение произвольного размера. Формально требование коллизионной устойчивости можно сформулировать так: Вычислительно неосуществимо нахождение двух сообщений M и M M для H ( M ) H ( M ) , которых с существенной вероятностью выполняется условие. Оно называется также строгим (или сильным) требованием коллизионной стойкости. Формулируют также требование слабой коллизионной стойкости: Для данного сообщения М, хэш-функция от которого равна /ДМ), вычислительно неосуществимо нахождение другого сообщения M M , для которого с существенной вероятностью выполняется условие H (M ) H ( M ). Очевидно, что хэш-функция, стойкая к коллизиям в строгом смысле, является стойкой и в слабом смысле. Но хэш-функция, стойкая к коллизиям в слабом смысле, не всегда является стойкой к коллизиям в строгом смысле. Для того чтобы хэш-функция была устойчивой к коллизиям, необходимо, но не достаточно, чтобы она была труднообратимой. Функция называется труднообратимой, если выполняется следующее условие. Для случайно выбранного значения Н вычислительно неосуществимо нахождение сообщения М, хэш-функция от которого с существенной вероятностью была бы равна H, т.е. Н=Н(М). Иными словами, хэш-функция должна быть труднообратимой. Функция может быть труднообратимой, но не быть коллизионно устойчивой. Примером может служить функция возведения в дискретную степень по модулю большого простого x числа: Y mod p, где а — первообразный корень в поле вычетов по модулю р. При заданном случайном Y вычислительно сложно найти какое-либо значение X, которое бы соответствовало данному Y, хотя таких значений чрезвычайно много, если не ограничивать размер аргумента, что и имеет место в случае хэш-функций. Наибольший интерес представляют хэш-функции, являющиеся стойкими к коллизиям в строгом смысле. Если хэш-функция стойкая, то при любом изменении аргумента (т. е. входного сообщения) ее значение изменится псевдослучайным образом, а именно с вероятностью 1/2 изменится каждый из т битов двоичного вектора Н. Простейшей атакой на труднообратимую хэш-функцию является подбор сообщения, имеющего заданное значение хэш-функции Н. Оценим количество различных текстов (7V), от которых надо вычислить хэш-функцию, чтобы с вероятностью 1/2 среди них оказался текст с заданным значением хэш-функции. Вероятность того, что хэш-функция от некоторого произвольно выбранного текста не совпадет с заданным значением У, равна 1 2 m . Вероятность, что хэш-функция ни от одного из N различных текстов не совпадает с Н, равна p (1 2 m ) N . Вероятность того, что хэш-функция, по крайней мере, от одного из этих сообщений совпадает с H 0 , равна Используя формулу бинома Ньютона, получаем следующие приближения (1 x) N 1 Nx N ( N 1) 2 n( N 1)( N 2) 3 x x ... 1 Nx, p N * 2 m иN p * 2 m 2! 3! если А" мало. При р = 1/2 имеем N 2 m1 . В настоящее время для значения т = 64 такая лобовая (силовая) атака может быть реализована организацией, имеющей сравнительно большие вычислительные ресурсы. При т>96 битов труднообратимая хэш-функция является стойкой к такой атаке, однако существуют и другие варианты атак (см. раздел 6.4), которые диктуют необходимость использования значений m 128 Для того чтобы иметь возможность вычислять хэш-функции от сообщений произвольного размера, используют разбиение блока данных на подблоки одинакового размера: M (M 1 , M 2 ,..., M n ) , где п — число подблоков длины т бит. Если длина исходного сообщения не кратна т, то оно дополняется до кратной длины по некоторому заранее оговоренному правилу, задающему однозначность дополнения. Один из способов построения хэш-функций состоит в использовании некоторого итеративного механизма на базе блочного одностороннего преобразования или стойкой шифрующей H i E ( H i 1 , M i ), i 1,2,..., n, функции Е с n-битовым входом: где H 0 — некоторое специфицированное начальное значение, M i — блоки сообщения, используемые в качестве ключа. Значение H H n принимается за значение хэш-функции, которую можно записать в виде H H ( H 0 , M ) , что подчеркивает зависимость Н от начального параметра H 0 . В таких схемах построения стойкость хэш-функций не превышает стойкости базовой итеративной функции Е, что делает необходимым применение криптографически стойких базовых функций. Не представляет труда изменить преобразования, используемые в некоторой стойкой хэш-функции, таким образом, чтобы они зависели от секретного ключа или использовали некоторые секретные параметры, однако такие хэш-функции не настолько широко применяются, как бесключевые хэш-функции. Если имеется стойкая бесключевая хэш- функция, то она очень просто может быть преобразована в хэшфункцию с ключом. Достаточно дополнительно использовать зашифрование полученного значения хэш-функции с помощью некоторого известного блочного шифра. Несомненно, что использование секретных элементов в хэш-функциях делает их более стойкими, однако во многих случаях требуются бесключевые хэш-функции. В первую очередь это касается систем ЭЦП, прочно вошедших в широкое применение.