Заметим, что аналогичное соотношение было принято в

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
«ВЫСШАЯ ШКОЛА ЭКОНОМИКИ»
Московский институт электроники и математики
ДОРОФЕЕВ ПЕТР АРКАДЬЕВИЧ
О НЕКОТОРЫХ ПРОБЛЕМАХ ПОСТРОЕНИЯ И АНАЛИЗА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ФУНКЦИОНИРОВАНИЯ РЕГУЛИРУЕМОГО ПЕРЕКРЕСТКА В СОВРЕМЕННОМ МЕГАПОЛИСЕ
Выпускная квалификационная работа
студента образовательной программы бакалавриата
01.03.04 Прикладная математика
Студент группы № М-72
Дорофеев П.А.
Научный руководитель
Кандидат физ.-мат. наук, доцент.
Шнурков Петр Викторович
Москва 2015 г.
Оглавление
Введение ............................................................................................... 3
Проблемы управления движением в Москве. ................................... 3
Глава 1. Обзор научных результатов, связанных с разработкой
оптимальной организации уличного движения в крупных городах . 4
§1. Краткое описание истории создания теории оптимальной
организации уличного движения. .................................................... 4
§2. Основные модели, используемые в теории оптимальной
организации уличного движения. .................................................... 5
§3. О проблеме регулируемого пересечения городских магистралей и
общих подходах к ее исследованию. ............................................. 12
Глава 2. Разработка и анализ стохастической модели ОДД на
многополосном перекрестке ............................................................. 17
§1. Общее описание исследуемой системы и ее основные
характеристики ................................................................................. 17
§2. Стохастические объекты, связанные с рассматриваемой системой, и
их вероятностные характеристики. ................................................. 19
Заключение ......................................................................................... 28
Список литературы ............................................................................. 29
2
Введение
Транспортная
инфраструктура
играет
важную
роль
в
обеспечении
нормального функционирования и жизнедеятельности городов. В развитых странах
на развитие транспортной инфраструктуры тратится существенный процент ВВП.
Чтобы инвестиции были эффективными, необходимо просчитывать все параметры и
закономерности транспортных сетей. В противном случае неизбежно возникновение
дисбаланса в сети, что приводит к постоянным заторам, перегрузкам и
экологическому
ущербу.
Для
оптимального планирования были привлечены специалисты из разных областей –
физики, математики, специалисты по транспорту, экономисты и др.
Проблемы управления движением в Москве.
В недавнем интервью бизнес-изданию РБК [21] заместитель мэра Москвы по
вопросам транспорта Максим Ликсутов охарактеризовал общие проблемы ОДД
(здесь и далее - организации дорожного движения) в Москве и, в частности,
довольно ясно описал причинно-следственную связь заторов и факторов,
вызывающих их.
М. Ликсутов отметил, что в настоящее время существует созданная по заказу
Правительства Москвы интеллектуальная транспортная система, позволяющая
проанализировать
маршруты
передвижения
автомобилей,
посчитать
в
количественном отношении транспортные потоки. Собранные данные можно
использовать для “изменения работы светофоров, введения одностороннего режима
движения”.
Для того, чтобы данная система функционировала и развивалась, необходимы
теоретические разработки функционирования транспортных узлов, перекрестков,
магистралей и тд.
3
Глава 1. Обзор научных результатов, связанных с разработкой
оптимальной организации уличного движения в крупных городах
§1. Краткое описание истории создания теории оптимальной
организации уличного движения.
Пионером в области научного исследования проблемы и адаптации городской
инфраструктуры к неизбежному увеличению числа автомобилей является русский
ученый Г. Д. Дубелир. В его трудах «Планировка городов» [2, 1910 год] и «Основы
проектирования автомобильных дорог» [3, 1937 год] были впервые рассмотрены
вопросы оптимизации сети автомобильных дорог.
Первое исследование проблемы функционирования транспортных потоков и
описания движения АТС (здесь и далее АТС - автотранспортные средства),
основанное на идеях и методах теории вероятностей выполнил Адамс в 1936 году
[10]. В это же время в Бюро Дорожного Движения Йельского университета Брюс
Гриншильдс [14] предложил аналоговый метод в исследовании потоков АТС.
После Второй Мировой Войны взрывной рост числа автомобилей в городах, а
также неминуемое увеличение городских автотранспортных сетей поднял на новый
уровень изучение транспортных потоков. В 50-х годах XX века были созданы и
исследованы
первые математические модели
функционирования дорожного
движения в городах. Эти модели были связаны с такими областями науки как
волновая теория и теория очередей (теория массового обслуживания), а также
появившейся как самостоятельная теория - теория следования за лидером.
Наиболее известная математическая модель динамики транспортного потока
была разработана и исследована Лайтхиллом, Уиземом [16] и, независимо,
Ричардсом в 1955 г. [20]. В научной литературе эта модель получила краткое
название - LWR (Lighthill-Whitham-Richards).
Параллельно, увидели свет труды таких ученых, как Ньюэлл [18, 1962год],
Вэбстер (1957), Чендлер (1958) и другие.
4
К концу 50х годов развитие теории транспортных потоков вышло на тот
уровень, при котором необходимо было провести международный семинар для
обмена опытом и идеями. В 1959 году на базе исследовательской лаборатории
General Motors был проведен симпозиум по Теории Транспортных потоков. В
последующие десятилетия данные мероприятия проводились регулярно, в том числе
на базе калифорнийского университета Беркли.
В нашей стране серьезные работы по исследованию автотранспортных
потоков были впервые представлены на механико-математическом факультете МГУ
им. М. В. Ломоносова в конце 70х годов XX века, перед Олимпиадой-80 в Москве.
В настоящее время, изучением Теории транспортных потоков занимаются
ведущие институты и лаборатории мира. Выпускаются специализированные
академические журналы, посвященные автомобильному движению. Власти США
отнесли проблемы транспортных систем к проблемам национальной безопасности и
используют самую современную технику для исследований в Национальной
исследовательской лаборатории Лос-Аламос (штат Нью-Мексико).
В Российской Федерации над проблемой динамики дорожного движения
работают в МИФИ, Новосибирском Государственном Университете, МГУ им. М. В.
Ломоносова, НИУ ВШЭ, Томском Государственном Университете, Институте
системного анализа РАН, МАДИ, МГТУ им. Баумана, Институте прикладной
математики им. М. В. Келдыша, ЦИТИ и др.
§2.
Основные
модели,
используемые
в
теории
оптимальной
организации уличного движения.
Исторически, в процессе развития сформировалось два традиционных подхода
к моделированию движения АТС. Макроскопический подход основан на моделях и
методах теоретической и математической физики, а именно таких направлений как
гидро- и газовая динамика. В микроскопическом подходе предполагается, что
каждый автомобиль представляет собой отдельный дискретный случайный объект,
и его движение определяется случайными факторами. Принцип построения моделей
5
основан на таких областях науки как механика взаимодействия твердых тел,
стохастический анализ, в частности теория массового обслуживания (в зарубежной
литературе
–
теория
очередей),
а
также
имитационное
компьютерное
моделирование.
Макроскопические (детерминированные) модели
Макроскопический подход к математическому моделированию транспортных
потоков используется для описания движения транспорта на расстояниях, во много
раз превосходящих размеры самих автомобилей. При этом плотность самих потоков
достаточно велика. В такой ситуации всем водителям приходится придерживаться
одинаковой стратегии поведения. Скорость потоков далека от скорости свободного
движения. Такие модели были названы также моделями-аналогами, так как
движение транспортных средств рассматривается как движение физического потока,
например слабосжимаемой жидкости. В основе макроскопических моделей лежит
функциональная зависимость между скоростью и дистанцией.
Далее рассмотрим некоторые наиболее известные из этих моделей (отметим,
что в работах [1] и [9] содержатся библиографические очерки с описанием
существующих макроскопических моделей).
Модель Гриншилдса и Гринберга
Данная модель изложена в работах [13] и [14]. Для описания этой
гидродинамической модели вводятся усредненные характеристики, такие как
скорость автомобилей 𝑣(𝑥, 𝑡) и плотность потока 𝜌(𝑥, 𝑡) − число автомобилей на
единицу длины дороги в момент времени 𝑡. Количество автомобилей, находящихся
в области (𝑥1 , 𝑥2 ) в момент времени 𝑡 выражается в форме интеграла от плотности
потока:
𝑥2
∫ 𝜌(𝑥, 𝑡)𝑑𝑥
𝑥1
6
В теории известно уравнение изменения плотности, показывающее, как
въезжающие и выезжающие автомобили изменяют общее число АТС на интервале
(𝑥1 , 𝑥2 ):
𝑥2
𝑑
∫ 𝜌(𝑥, 𝑡)𝑑𝑥 = 𝜌(𝑥1 , 𝑡)𝑣(𝑥1 , 𝑡) + 𝜌(𝑥2 , 𝑡)𝑣(𝑥2 , 𝑡)
𝑑𝑡
𝑥1
Полагая, что 𝜌 и 𝑣 - непрерывные функции, проинтегрируем это соотношение
по времени:
𝑡2 𝑥2
∬
𝑡1 𝑥1
𝜕𝜌(𝑥, 𝑡)
𝑑𝑥𝑑𝑡
𝜕𝑡
𝑡2
= ∫ (𝜌(𝑥1 , 𝑡)𝑣(𝑥1 , 𝑡) + 𝜌(𝑥2 , 𝑡)𝑣(𝑥2 , 𝑡))𝑑𝑥𝑑𝑡
𝑡1
𝑡2 𝑥2
= − ∬ [
𝑡1 𝑥1
𝜕(𝜌(𝑥, 𝑡)𝑣(𝑥, 𝑡))
] 𝑑𝑥𝑑𝑡
𝜕𝑡
Так как 𝑡1 𝑡2 > 0, 𝑥1 𝑥2 ∈ ℝ , вышестоящее уравнение перепишется в виде:
𝜌𝑡 + (𝜌𝑣)𝑥 = 0
(1.1)
Начальные условия: 𝜌(𝑥, 0) = 𝜌0 (𝑥)
Далее найдем выражение для скорости 𝑣. Пусть 𝑣 зависит только от 𝜌.
Очевидно, что если 𝜌 = 0 (отсутствие АТС), то 𝑣 = 𝑣𝑚𝑎𝑥 .
Верно и обратное: при 𝜌 = 𝜌𝑚𝑎𝑥 , 𝑣 = 0. В этом случае известна следующая
формула, которая была получена Б. Гриншилдсом [14]:
𝜌
𝑣𝑚𝑎𝑥 (𝜌) = 𝑣 (1 −
) , 0 ≤ 𝜌 ≤ 𝜌𝑚𝑎𝑥
𝜌𝑚𝑎𝑥
Тогда соотношение (1.1) примет вид:
𝜌
𝜌𝑡 + [𝑣𝑚𝑎𝑥 𝜌 (1 −
)] = 0, 𝑥 ∈ ℝ, 𝑡 > 0
𝜌𝑚𝑎𝑥
Этот закон был назван "законом сохранения автомобилей".
7
(1.2)
Позже, Гринберг построил модель, в которой уравнение Гриншилдса (1.2)
является частным случаем.
Подставим (1.1) в уравнение изменения скорости потока во времени:
𝑑𝑣
𝑑𝑣 𝑑𝑣
= −𝜌 ( )
𝑑𝑡
𝑑𝑥 𝑑𝜌
Так как по предположению
𝑣 = 𝑣[𝜌(𝑥(𝑡), 𝑡)]
(1.3)
соотношение (1.3) можно переписать в виде
𝑑𝑣
𝑑𝑣 2 𝜕𝜌
= −𝜌 ( )
𝑑𝑡
𝑑𝜌 𝜕𝑥
Из гидродинамики известно аналогичное уравнение для несжимаемой
жидкости, выведенное Эйлером:
𝑑𝑣
𝜕𝜌
= −С2 𝜌𝑛
𝑑𝑡
𝜕𝑥
(1.4)
Решением уравнения (1.4) для задачи с потоком транспорта будет следующее
выражение, впервые полученное Гринбергом :
𝜌𝑚𝑎𝑥
𝐶𝑙𝑛
,
𝑛 = −1
𝜌
𝑣={
𝑛+1
𝑛+1
𝐶
[𝜌𝑚𝑎𝑥 2 − 𝜌 2 ] , 𝑛 ≠ −1
𝑛+1
𝐶 = 𝑐𝑜𝑛𝑠𝑡
Модель Гриншилдса (1.2) является частным случаем модели Гринберга [13]
𝑛 = 1:
𝜌
𝑛+1
2
𝑣 = 𝑣0 (1 − [
]
𝜌𝑚𝑎𝑥
)
где 𝑣0 - скорость при 𝜌 = 0
Модель Лайтхилла-Уизема-Ричардса [16, 20]
В
данной
модели
предполагается,
что
существует
функциональная
зависимость между скоростью и плотностью для того, чтобы учесть изменение
скорости движения потока АТС с ростом его плотности.
8
Средняя скорость потока есть функция плотности
𝑣(𝑥, 𝑡) = 𝑣𝑒 [𝜌(𝑥, 𝑡)]
Сама трасса - есть однополосная, однонаправленная дорога.
Лайтхилл и Уизем вывели следующее уравнение:
𝜌𝑡 + 𝑐(𝜌)𝜌𝑥 = 0
(1.5)
где 𝑐(𝜌) = 𝑄′ (𝜌) = 𝑣𝑒 (𝜌) + 𝜌𝑣 ′ 𝑒 (𝜌) - скорость распространения возмущений
Соотношение
𝑄(𝜌) = 𝜌𝑣𝑒 (𝜌) задает
фундаментальную
диаграмму
и
показывает, что пропускная способность дороги определяется плотностью потока.
Общий вид решения (1.5):
𝑐(𝑥, 𝑡) = 𝐹(𝑥 − 𝑣𝑡)
- описывает бегущую волну, взятую из природы кинематических волн.
Модель Пэйна
Модель Лайтхилла-Уизема предполагает значение скорости равновесным, что,
на практике, совсем не так. Практически на всех дорогах присутствуют сужения и
съезды, при проезде которых скорость АТС неравновесна. Поэтому, Пэйном [19]
было предложено дифференциальное уравнение для описания динамики средней
скорости в неравновесных ситуациях [1], [9]:
𝜕(𝜌𝑣) 𝜕(𝜌𝑣 2 + 𝑃(𝜌))
1
+
= − (𝜌𝑣 − 𝜌𝑉(𝜌))
𝜕𝑡
𝜕𝑥
𝜏
1
(1.6)
𝜌
где 𝑃(𝜌) = ∫0 𝐷(𝜑)𝑑𝜑
𝜏
По своему физическому содержанию, уравнение(1.6) - есть закон изменения
импульса в дивергентной форме.
Микроскопические (стохастические) модели
С позиции микроскопического подхода к моделированию, транспортный
поток рассматривается как вероятностный процесс. Когда мы рассматриваем
каждый автомобиль в отдельности, со своими правилами поведения и обращаем
внимание на расстояния
между соседними
микроскопический принцип моделирования.
Нелинейная модель следования за лидером
9
авто,
то
используем
именно
Одна из первых моделей данного типа была предложена сотрудниками
концерна General Motors Д. Газисом и Р. Херманом [1], [9]. В качестве основы для
построения модели взяли однополосный транспортный поток и гипотезу о том, что
движение любого автомобиля в потоке ограниченно впереди идущим автомобилемлидером.
В начале предполагалось, что каждый водитель согласует свою скорость с
ведущим автомобилем так, что выполняется соотношение:
1
𝑥𝑖+1
̈ (𝑡) = (𝑥̇ 𝑖 (𝑡) − 𝑥̇ 𝑖+1 (𝑡))
𝜏
(1.7)
Где 𝜏 - время согласования скоростей, 𝑥𝑖 - координата автомобиля-лидера.
В дальнейшем, модель усовершенствовали, добавив время реакции водителя
на изменение скорости автомобиля-лидера. В итоге, команда исследователей из GM
модифицировала уравнение (1.7):
𝑥̈ 𝑖+1 (𝑡 + 𝑡𝑑 ) = 𝛼(𝑥̇ 𝑖+1 (𝑡 + 𝑡𝑑 ))𝑛1
𝑥̇ 𝑖 (𝑡) − 𝑥̇ 𝑖+1 (𝑡)
(𝑥𝑖 (𝑡) − 𝑥𝑖+1 (𝑡))𝑛2
добавив оценку коэффициентов 𝑛1 и 𝑛2 по итогам экспериментов.
Подстановка самых простых чисел 𝑛1 = 0 и 𝑛2 = 0 дает следующий результат,
использующийся для аналитических исследований:
𝑥̈ 𝑖+1 (𝑡 + 𝑡𝑑 ) = 𝛼
𝑥̇ (𝑡) − 𝑥̇ 𝑖+1 (𝑡)
𝑥𝑖 (𝑡) − 𝑥𝑖+1 (𝑡)
(1.8)
Проинтегрировав (1.8), получим:
𝑥̇ 𝑖+1 (𝑡 + 𝑡𝑑 ) = ln (𝜌𝑚𝑎𝑥 (𝑥𝑖 (𝑡) − 𝑥𝑖+1 (𝑡)))
где 𝜌𝑚𝑎𝑥 – постоянная величина, значение которой характеризует движение
автомобилей близко друг к другу.
Как и в предыдущих моделях, плотность потока выражается через 𝜌 и в
данной модели задается формулой:
𝜌=
1
𝑥𝑖 (𝑡) − 𝑥𝑖+1 (𝑡)
10
Тогда выражение для скорости будет выглядеть следующим образом:
1 𝜌𝑚𝑎𝑥
𝑣 = 𝑙𝑛
𝜏
𝜌
Данное выражение совпадает с известным нам результатом из модели
Гринберга [13]. Совпадение результатов, получаемых при исследовании различных
моделей, означает, что эти подели по-разному, но в целом правильно отражают
объективную реальность.
Модель, основанная на теории клеточных автоматов.
Клеточные
автоматы
-
пример
дискретных
динамических
систем,
пространство которых представлено сеткой, с ячейками одинакового размера.
Первая модель, использующая теорию клеточных автоматов (КА), была разработана
Фон Нейманом, при попытке создать самовоспроизводящихся роботов. Позже,
Нагель и Шрекенберг [17] применили теорию КА к решению транспортных задач. В
первоначальном варианте данная модель была предназначена для описания
функционирования однополосной дороги, где каждая ячейка была свободным или
занятым участком. Рассмотрим подробнее данную концепцию.
Обозначим за 𝑥𝑖 и 𝑣𝑖 обозначили координату и скорость -го автомобиля, 𝑑𝑖 =
𝑥𝑖+1 − 𝑥𝑖 - дистанцию до лидирующего автомобиля. Скорость принимает одно из
𝑣𝑚𝑎𝑥 + 1 допустимых значений, где 𝑣𝑖 = 0,1, … 𝑣𝑚𝑎𝑥 . В каждый новый момент
времени состояние автомобилей в системе обновляется (происходит перемещение
автомобилей на соответствующее число ячеек)
Динамика модели или эволюция данной системы во времени описывается
следующим образом:
Шаг 1: Ускорение Если 𝑣𝑖 < 𝑣𝑚𝑎𝑥 , 𝑣𝑖 увеличивается на 1. В противном случае
𝑣𝑖 остается неизменной.
По-сути, данный шаг показывает стремление водителя ехать быстрее.
Шаг 2: Торможение Если 𝑑𝑖 ≤ 𝑣𝑖 , то -й автомобиль сбрасывает скорость до
𝑑𝑖 − 1.
Соблюдение
данного
правила
автомобилем, движущимся впереди.
11
позволит
избежать
столкновений
с
Шаг 3: Случайные возмущения Если текущая скорость 𝑖 автомобиля больше 0,
то она может быть уменьшена на единицу с вероятностью 𝑝, в противном случае
скорость остается неизменной.
Шаг 4: Движение После выполнения шагов 1-3, каждый автомобиль
продвигается вперед на количество ячеек, соответствующее приобретенной после
шагов 1-3 скорости.
Таким образом, изложенная выше модель отражает основные свойства
транспортного потока. В частности, она позволяет прогнозировать динамику потока
и вычислять его различные характеристики.
§3. О проблеме регулируемого пересечения городских магистралей и
общих подходах к ее исследованию.
Одной из наиболее актуальных и малоизученных областей в исследовании
транспортных потоков является анализ пересечений транспортными средствами
автомобильных дорог по перекресткам, сужениям и пр. Существует два
направления работ, в которых исследуется регулируемое пересечение магистралей.
В первом случае объектом изучения служит отдельный перекресток, во втором –
взаимосвязанная система перекрестков.
В данной работе будет представлена модель исследования первого типа.
Отдельным или изолированным перекресток является тогда, когда его процесс
функционирования не зависит от
работы светофоров и правил организации
движения на соседних перекрестках.
Введем
основные
понятия,
используемые
в
моделях.
Ключевыми
характеристиками главного регулятора на перекрестке - светофорной сигнализации
являются такт, фаза и цикл. Тактом называется интервал времени, в течение
12
которого разрешено движение одному из конкурирующих направлений (возможно и
нескольким другим второстепенным). Для каждого направления можно определить
основной такт и промежуточные, в течение которых потоку практически (по
основному направлению) запрещено движение. Совокупность основного и
промежуточного такта называется фазой. Периодически повторяющийся набор фаз
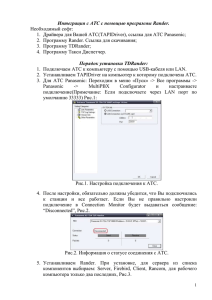
называется циклом [6], (см Рис.1).
Рис. 1
Рисунок 1 представляет собой форму изобразительного, наглядного описания
функционирования
системы
регулируемого
перекрестка.
Функционирование
системы происходит циклически, циклы повторяются и одинаковы по своей
структуре. Каждый цикл состоит из двух фаз. Первая фаза включает два такта. На
первом такте по первому направлению движение разрешено, а по второму
запрещено. Второй такт является промежуточным, по обоим направлениями
установлен предупредительный желтый сигнал. Первый и второй такты образуют
первую фазу. Вторая фаза также состоит из двух тактов: третьего и четвертого. На
третьем такте по первому направлению движение запрещено, а по второму
разрешено, т.е. ситуация зеркально отражает события на первом такте. Четвертый
такт вновь является промежуточным; по обоим направлениям установлен желтый
сигнал. Вторая фаза завершает цикл, в момент ее окончания начинается следующий
цикл, который идентичен предыдущему, т.е. имеет ту же самую структуру.
При исследовании проблемы оптимизации регулирования светофорной
сигнализации и увеличения пропускной способности перекрестка, была рассмотрена
13
зависимость пропускной способности, величины образовавшегося затора и время
ожидания от светофорных режимов.
К настоящему времени, с использованием численного моделирования удалось
уточнить и дополнить данный раздел новыми решениями для многополосных АТС.
Основополагающим научным исследованием в области теории отдельного
регулируемого перекрестка является работа американского ученого Дональда Р.
МакНила, опубликованная в 1968 году [11] и в дальнейшем адаптированная для
неспециалистов [12].
В работе [11] рассматривается перекресток, управляемый светофором с
фиксированным временем горения красного (𝑟) и зеленого (𝑔) сигналов светофора.
Движение на перекрестке в целом происходит согласно схеме, представленной на
рис. 1. Отметим, что в основу математической модели положена общая
конструкция, используемая в теории массового обслуживания.
Процессы прибытия АТС на перекресток считаются Пуассоновскими. Отсюда
следует, что интервалы времени между моментами прибытия АТС на перекресток
независимы и имеют экспоненциальное распределение с заданным параметром.
Светофоры играют роль обслуживающих устройств.
МакНил вывел формулу, определяющую ожидаемую задержку при проезде
перекрестка с постоянным временем убытия. Общая транспортная задержка за 1
сигнальный цикл выражается через сумму двух компонент:
𝑊 = 𝑊1 + 𝑊2
(1.9)
где
𝑊1 - задержка на красной фазе горения светофорной сигнализации
𝑊2 - задержка на зеленой фазе горения светофорной сигнализации.
Рассмотрим подробнее данную модель.
Обозначим через 𝑄(𝑡) - количество АТС, скопившееся в очереди за время
горения красного сигнала к моменту времени 𝑡, 𝐴(𝑡)- число АТС, подъехавших к
перекрестку за время 𝑡.
14
Обозначим через 𝑐 общее время сигнального цикла, 𝑔 - время горения
зеленого сигнала светофора (величины 𝑐 и
𝑔 предполагаются заданными и
детерминированными).
Имеют место следующие формулы для случайных длительностей задержки:
𝑐−𝑔
𝑊1 = ∫ [𝑄(0) + 𝐴(𝑡)]𝑑𝑡
(1.10)
0
𝑐
𝑊2 = ∫ 𝑄(𝑡)𝑑𝑡
𝑐−𝑔
Используя свойства Пуассоновсого процесса, выразим математическое
ожидание (1.10):
1
𝐸(𝑊1 ) = (𝑐 − 𝑔)𝑄0 + 𝑞(𝑐 − 𝑔)2
2
Введем переменную 𝑍 - полное время ожидания, необходимое для
обслуживания АТС, количество которых в очереди отражает процесс 𝑄(𝑡); при этом
процесс прибытия АТС в очередь релевантен сложным Пуассоновским процессам, с
1
постоянным временем обслуживания .
𝑆
(1 + 𝐼𝑞 ⁄𝑆 − 𝑞⁄𝑆)𝐸[𝑄(𝑡0 )]
𝐸[𝑄2 (𝑡0 )]
𝐸(𝑍) =
+
2𝑆(1 − 𝑞⁄𝑆)2
2𝑆(1 − 𝑞⁄𝑆)
Математическое ожидание может быть выражено следующим образом:
𝐸(𝑊2 ) = 𝐸[𝑍|𝑄(𝑡 = 𝑐 − 𝑔)] − 𝐸[𝑍|𝑄(𝑡 = 𝑐)]
Тогда явно выразим 𝐸(𝑊2 ):
(1 + 𝐼𝑞 ⁄𝑆 − 𝑞⁄𝑆)𝐸[𝑄(𝑐 − 𝑔)] − 𝐸[𝑄(𝑐)] 𝐸[𝑄2 (𝑐 − 𝑔)]−𝐸[𝑄2 (𝑐)]
𝐸(𝑊2 ) =
+
2𝑆(1 − 𝑞⁄𝑆)2
2𝑆(1 − 𝑞⁄𝑆)
Далее явно выражаем числители в обоих слагаемых и получаем следующую
формулу:
15
𝐸(𝑊2 ) =
1
((1 + 𝐼 𝑞⁄𝑆 − 𝑞⁄𝑆)𝑔(𝑐 − 𝑔) + (1 − 𝑞⁄𝑆)(2𝑞(𝑐 − 𝑔)𝑄0 ))
2𝑆(1 − 𝑞⁄𝑆)2
+
1
(𝑞 2 (𝑐 − 𝑔)2 + 𝑞(𝑐 − 𝑔)𝐼)
2𝑆(1 − 𝑞⁄𝑆)
Подставляя полученные выражения для 𝑊1 и 𝑊2 в исходную формулу (1.9)
получим окончательную формулу средней задержки АТС на перекрестке:
𝐸(𝑊) =
(𝑐 − 𝑔) 𝑄0
𝑐−𝑔
1
𝐼
[ +(
) 𝑞𝑐 + (1 +
)]
𝑐(1 − 𝑞⁄𝑆) 𝑞
2
𝑆
1 − 𝑞 ⁄𝑆
Данная формула представляет собой основной результат работы [11].
Замечания: Приведенная выше модель имитирует ситуацию на регулируемом
перекрестке двух однополосных дорог. У обслуживающего устройства (светофора)
всего два режима работы: красный и зеленый. Соответственно один цикл содержит
только две фазы: горение красного и зеленого сигналов. На практике, таких
пересечений практически нет. В современных городах регулируемые перекрестки
являются развязками для трех, четырех, а то и шести направлений одновременно.
Поэтому к моделированию реальной ситуации вывод Мак Нила применить нельзя.
В то же время, модель, разработанная Мак Нилом, может быть развита и
усложнена. Построение и анализ такой усложненной модели проводится в
следующей главе настоящей работы. Предлагаемая новая модель, использующая
идеи модели Мак Нила, позволяет описывать реальные системы организации
движения на перекрестках в крупных современных городах.
16
Глава 2. Разработка и анализ стохастической модели ОДД на
многополосном перекрестке
§1.
Общее
описание
исследуемой
системы
и
ее
основные
характеристики
Начнем наше изложение с основных понятий и обозначений, используемых
при построении математической модели функционирования системы ОДД на
перекрестке.
𝐴(𝑡) - число АТС, поступивших в систему за время t от начального момента
𝑐𝑖 - длительность i фазы (детерминированная величина)
𝑑 - средняя задержка.
𝑔 - эффективное время горения зеленого сигнала.
𝑞 - параметр входящего потока, т.е. математическое ожидание числа АТС,
поступающих за единицу времени.
𝑄0 - число АТС, оставшихся недообслужанными после предыдущих циклов.
𝑄(𝑡) - общее число АТС в системе в момент времени t.
𝑟 - эффективное время горения красного сигнала.
𝑆𝑖 - пропускная способность совокупности полос в i фазе, т. е. число АТС,
которые могут пройти перекресток в течение этой фазы при непрерывном
движении транспорта; величина 𝑆𝑖
предполагается детерминированной и
заданной.
𝑊 - общая суммарная случайная задержка в системе.
𝑊𝑖 - случайная задержка на i фазе.
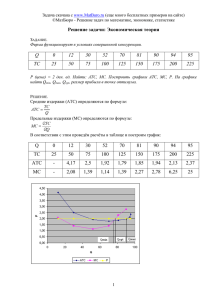
Построим математическую модель функционирования реальной системы
ОДД, расположенной на пересечении Ленинского проспекта и улицы Обручева в г.
Москве. Схема данного перекрестка представлена на Рис. 2
17
Рис. 2
Для
каждой
дороги
существуют
четыре
режима,
определяемых
соответствующим сигналом светофора. Фазы следуют одна за другой в строго
определенной последовательности. Порядок фаз определяется их номерами 1,2,3,4.
После завершения 4 фазы происходит переход к 1. Как было сказано в предыдущей
главе, период между началом первой фазы и концом последней называется циклом
функционирования.
Описание функционирования рассматриваемой системы, т.е. полное описание
возможных режимов работы, задается следующей Таблицей 1:
Табл. 1
Где знаки «стрелка» означают направления, по которым разрешено движение
для данной дороги на конкретной фазе работы светофорной сигнализации, а «круг» полное запрещение движения по всем направлениям
Анализ особенностей поведения системы, описанной указанной таблицей,
приводит к выводу, что убытие в каждой фазе для каждой дороги неравномерно - за
18
время горения разрешающего сигнала светофора для соответствующей дороги число
покинувших автомобилей меньше абсолютного значения пропускной способности
перекрестка.
Итак, с каждой фазой системы связана определенная задержка. В предыдущем
разделе работы было описано понятие задержки, связанной с каждой фазой. Фазы
последовательно сменяют друг друга. Естественно считать, что общая случайная
задержка, связанная с циклом из четырех фаз, должна быть равна сумме задержек по
каждой фазе. Таким образом должно выполняться соотношение:
𝐸𝑊 = 𝐸𝑊1 + 𝐸𝑊2 + 𝐸𝑊3 + 𝐸𝑊4,
(2.1)
где 𝑊 − общая задержка,
𝑊𝑖 − задержка, связанная с -фазой, 𝑖 = 1 … 4
Заметим, что аналогичное соотношение было принято в работе [11] для
модели с двумя фазами.
Перейдем к анализу отдельных фаз и определению их вероятностных
характеристик.
§2. Стохастические объекты, связанные с рассматриваемой системой,
и их вероятностные характеристики.
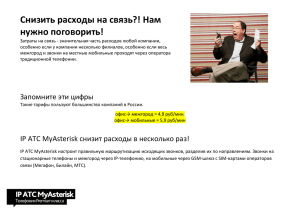
По аналогии с работой МакНила (McNeil'a [11]) введем случайный процесс
𝑄(𝑡), представляющий собой общее число АТС, находящихся в системе в момент
времени t. Как известно из [11], случайная длительность задержки по отдельной
фазе может быть выражена в форме интеграла от траектории процесса 𝑄(𝑡) (Схема
изображена на Рис.3).
Распространим этот подход на рассматриваемую систему.
Обозначим через 𝑐𝑖 длительность i-й фазы цикла, 𝑖 = 1 … 3
Заметим, что величины 𝑐𝑖 являются детерминированными и, фактически,
определяют режим работы светофорной сигнализации на перекрестке. Таким
образом,
параметры
𝑐𝑖 естественно
считать
рассматриваемой системе.
19
параметрами
управления
в
Рис. 3
В дальнейшем будем рассматривать величину средней суммарной задержки
𝐸(𝑊) как показатель качества функционирования исследуемой системы. Целью
последующего анализа будет получение явной зависимости величины 𝐸(𝑊) от
параметров 𝑐𝑖 , 𝑖 = 1 … 3
Перейдем к нахождению математических ожиданий 𝐸(𝑊𝑖 ), 𝑖 = 1. .4 входящих
в формулу (2.1).
Начнем с первой фазы функционирования системы. Будем предполагать, что
поступление АТС в систему описывается случайным пуассоновским процессом 𝐴(𝑡)
с заданным параметром 𝑞 > 0. Иначе говоря, 𝐴(𝑡) - есть число АТС, поступивших в
систему за время [0; 𝑡]. Тогда значение случайного процесса 𝑄(𝑡) может быть
выражено формулой
𝑄(𝑡) = 𝑄(0) + 𝐴(𝑡), где 𝑄(0) = 𝑄0 - значение случайного процесса 𝑄(𝑡) в
момент𝑡 = 0, то есть в момент начала рассматриваемого цикла. Предположим, что
данная величина является фиксированной.
Как уже отмечалось, имеет место связь между случайной величиной задержки
и траекторией процесса 𝑄(𝑡):
𝑐1
𝑐1
𝑊1 = ∫ 𝑄(𝑡)𝑑𝑡 = ∫ [𝑄(0) + 𝐴(𝑡)]𝑑𝑡
0
0
20
(2.2)
Интеграл в правой части формулы (2.2) понимается как стохастический
интеграл от траектории случайного процесса 𝑄(𝑡).
Воспользуемся свойством математического ожидания интеграла (см. [7] гл.1,
пар.2, теорема 1.9). Тогда из (2.2) следует:
𝑐1
𝐸𝑊1 = 𝐸[∫ (𝑄0 + 𝐴(𝑡))𝑑𝑡
0
𝑐1
𝑐1
𝑞𝑐1 2
= 𝑐1 𝐸𝑄0 + ∫ [𝐸𝐴(𝑡)]𝑑𝑡 = 𝑐1 𝑄0 + ∫ 𝑞𝑡𝑑𝑡 = 𝑐1 𝑄0 +
2
0
0
Обозначим для удобства
𝑖
𝑐̂𝑖 = ∑ 𝑐𝑘 , 𝑖 = 1, … 4; 𝑐0 = 0
𝑘=𝑜
тогда 𝑐̂1 = 𝑐1 , 𝑐̂2 = 𝑐1 +𝑐2 , 𝑐̂3 = 𝑐1 +𝑐2 + 𝑐3 , 𝑐̂4 = 𝑐
̂
Запишем формулы для приращений на интервале длительности [𝑐̂
𝑖−1 , 𝑐𝑖 ] 𝑖 =
1. .4:
𝑄(𝑐̂)
̂)
𝑖 = 𝑄(𝑐̂
𝑖−1 ) + [𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 𝑆𝑖
где
𝑄(𝑐̂
𝑖−1 ) - начальное значение процесса,
[𝐴(𝑐̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 )] - число требований, поступивших на данном интервале
(пуассоновская величина),
𝑆𝑖 - число обслуженных требований (величина детерминированная)
Сформулируем
общий
результат
для
представления
математических
ожиданий длительностей задержки на отдельных фазах функционирования
рассматриваемой системы обслуживания регулируемого перекрестка.
Теорема 1. Имеет место следующая формула для математического
ожидания задержки на i-й фазе функционирования системы:
2
2
𝐸[𝑄(𝑐̂)]
𝐸[𝑄(𝑐̂)
𝑖 − 𝐸[𝑄(𝑐̂
𝑖−1 )]
𝑖 ] − 𝐸[𝑄(𝑐̂
𝑖−1 ) ]
𝐸(𝑊𝑖 ) =
+
𝑞
𝑞 2
2𝑆𝑖 (1 − 𝑆 )
2𝑆𝑖 (1 − )
𝑖
𝑆𝑖
21
(2.3)
Доказательство.
Рассмотрим первую фазу функционирования системы. Пусть 𝑊𝑖 - задержка на
первой фазе.
Обозначим через 𝑍(𝑄(𝑡)) - случайное полное время ожидания, необходимое
для обслуживания АТС, находящихся в системе в некоторый момент времени 𝑡 в
течение одного периода занятости. Данная величина зависит от 𝑄(𝑡) - числа
требований в системе в момент 𝑡, т. е. определяется для любого фиксированного
значения 𝑄(𝑡). Обозначим такую величину 𝑍 при условии 𝑄(𝑡)) через 𝑍(𝑄(𝑡)).
Тогда величина задержки, возникающей на первой фазе:
𝑊1 = 𝑍(𝑄(𝑐1 )) − 𝑍(𝑄(𝑐0 ))
(2.4)
Будем обозначать в дальнейшем
𝐸𝑍(𝑄(𝑡)) = 𝐸[𝑍|𝑄(𝑡)] - условное математическое ожидание величины 𝑍 при
условии, что значение процесса 𝑄(𝑡) фиксировано.
Тогда из (2.4) следует, что математическое ожидание величины задержки
может быть записано следующим образом:
𝐸𝑊1 = 𝐸[𝑍|(𝑄(𝑐1 ))] − 𝐸[𝑍|(𝑄(𝑐0 ))]
(2.5)
Далее воспользуемся теоретическими результатами для общей модели
массового обслуживания со сложным пуассоновским входящим потоком и
детерминированной
длительностью обслуживания. В работе
[11]
доказана
следующая формула для математического ожидания случайной величины 𝑍,
зависящей от условия 𝑄(𝑡):
𝐸[𝑄(𝑡)]
𝐸[𝑄2 (𝑡)]
𝐸(𝑊1 ) =
+
2𝑆1 (1 − 𝑞⁄𝑆1 )2 2𝑆1 (1 − 𝑞⁄𝑆1 )
(2.6)
Из (2.5) и (2.6) следует:
𝐸[𝑄(𝑐1 )] − 𝐸[𝑄(0)] 𝐸[𝑄2 (𝑐1 )]−𝐸[𝑄2 (0)]
𝐸(𝑊1 ) =
+
2𝑆1 (1 − 𝑞⁄𝑆1 )2
2𝑆1 (1 − 𝑞⁄𝑆1 )
(2.7)
В формулах (2.6), (2.7) используются уже известные обозначения:
𝑞 - интенсивность входящего потока,
22
𝑆1 - число требований, обслуженных за рассматриваемый период времени
длительности 𝑐1 .
Теперь применим общие результаты анализа модели массового обслуживания,
рассмотренной в работе [11], для получения формул для математических ожиданий
длительностей задержек остальных фаз с номерами 𝑖 = 2 … 4. Обозначим через 𝑐𝑖 длительность 𝑖 -й фазы, а через 𝑆𝑖 - число требований (АТС), обслуженных в
системе в течение 𝑖 -й фазы (в силу специфики модели, 𝑆𝑖 является заданной
детерминированной величиной 𝑖 = 2 … 4. По аналогии с (2.5) имеем формулу для
математического ожидания длительности задержки на 𝑖 -й фазе:
𝐸𝑊𝑖 = 𝐸[𝑍|(𝑄(𝑐̂))]
− 𝐸[𝑍|(𝑄(𝑐̂
𝑖
𝑖−1 ))]
(2.8)
где полагаем 𝑐0 = 0.
Воспользуемся формулой (2.6) для моментов времени окончания фаз:
𝐸[𝑄(𝑐̂)]
𝐸[𝑄2 (𝑐̂)]
𝑖
𝑖
𝐸[𝑍|𝑄(𝑐̂)]
=
+
𝑖
2
2𝑆𝑖 (1 − 𝑞⁄𝑆𝑖 )
2𝑆𝑖 (1 − 𝑞⁄𝑆𝑖 )
(2.9)
𝑖 = 1…3
Из (2.8) и (2.9) получаем общую формулу для математического ожидания
задержки на i-й фазе:
𝐸(𝑊𝑖 ) =
2
2
𝐸[𝑄(𝑐̂)]
𝐸[𝑄(𝑐̂)
𝑖 − 𝐸[𝑄(𝑐̂
𝑖−1 )]
𝑖 ] − 𝐸[𝑄(𝑐̂
𝑖−1 ) ]
+
𝑞
𝑞 2
2𝑆𝑖 (1 − 𝑆 )
2𝑆𝑖 (1 − )
𝑖
𝑆𝑖
Теорема 1 доказана.
Для определения полной случайной задержки необходимо найти выражения
для числителей (2.3) в явном виде.
Заметим предварительно, что случайный процесс 𝑄(𝑡) обладает следующим
свойством: величины 𝑄(𝑐̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 ) являются независимыми.
Действительно, в соответствии с принятой моделью имеет место соотношение
𝑄(𝑐̂)
̂)
𝑖 = 𝑄(𝑐̂
𝑖−1 ) + [𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 𝑆𝑖
(2.10)
Именно, число АТС в момент начала 𝑖 -фазы 𝑐̂𝑖 складывается из следующих
составляющих:
23
𝑄(𝑐̂
𝑖−1 ) – число АТС в момент начала 𝑖 -фазы 𝑐̂
𝑖−1 (Число АТС, оставшихся в
системе в момент 𝑐̂
𝑖−1 );
[𝐴(𝑐̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 )] – число АТС, поступивших в систему за период реализации 𝑖
-фазы;
𝑆𝑖 – число АТС, покинувших систему за период реализации 𝑖 -фазы;
Тогда
𝑄(𝑐̂)
̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 ) = [𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 𝑆𝑖
(2.11)
Процесс 𝐴(𝑡) является Пуассоновским, следовательно, его приращения на
непересекающихся интервалах времени
[𝑐̂
̂]
𝑖−1 ; 𝑐
𝑖 являются независимыми. В
рассматриваемой модели 𝑆𝑖 – заданные детерминированные величины. Отсюда
следует, что приращения 𝑄(𝑐̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 ) являются независимыми.
Обратим внимание на то, что указанное свойство процесса 𝑄(𝑡) выполняется
только для интервалов времени [𝑐̂
̂],
то есть для периодов прохождения
𝑖−1 ; 𝑐
𝑖
различных фаз. Для других интервалов времени соотношение (2.10), вообще говоря,
не выполняется, и аналогичные рассуждения провести нельзя.
Сформулируем лемму для вывода в явном виде числителя первого слагаемого
(2.3):
Лемма 1. Для рассматриваемой модели имеет место следующая формула для
математических ожиданий приращений процесса 𝑄(𝑡):
𝐸[𝑄(𝑐̂)]
𝑖 − 𝐸[𝑄(𝑐̂
𝑖−1 )] = 𝑐𝑖 𝑞 − 𝑆𝑖
Доказательство. Из соотношения (2.11) следует, что
𝐸[𝑄(𝑐̂)
̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 )] = 𝐸[𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 𝑆𝑖
(2.12)
По свойству Пуассоновского процесса для любого интервала времени (𝑡, 𝑡 +
𝛿), 𝛿 > 0 имеет место:
𝐸[𝐴(𝑡 + 𝛿) − 𝐴(𝑡)] = 𝑞𝛿
Таким образом, из (2.12) получаем
𝐸[𝑄(𝑐̂)]
𝑖 − 𝐸[𝑄(𝑐̂
𝑖−1 )] = 𝑐𝑖 𝑞 − 𝑆𝑖
Лемма 1 доказана.
24
Лемма 2. Для рассматриваемого случайного процесса 𝑄(𝑡) имеет место
следующее равенство:
2
2
2 2
̂
𝐸𝑄2 (𝑐̂)
𝑖 − 𝐸𝑄 (𝑐̂
𝑖−1 ) = 2[𝑄0 + 𝑞𝑐̂
𝑖−1 − 𝑆𝑖−1 ](𝑞𝑐𝑖 − 𝑆𝑖 ) + 𝑞 𝑐𝑖 + 𝑞𝑐𝑖 − 2𝑆𝑖 𝑞𝑐𝑖 + 𝑆𝑖
Доказательство. Воспользуемся равенством
𝑄(𝑐̂)
̂)
𝑖 = 𝑄(𝑐̂
𝑖−1 ) + [𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )], 𝑖 = 1,2,3,4; 𝑐̂0 = 0
(2.13)
Причем 𝑄(𝑐̂0 ) = 𝑄(0) = 𝑄0 – фиксированное
𝐸𝑄(𝑐̂)
̂)
̂)
𝑖 = 𝐸𝑄(𝑐̂
𝑖−1 ) + 𝐸[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] = 𝐸𝑄(𝑐̂
𝑖−1 ) + 𝐸[𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 ) − 𝑆𝑖 ]
= 𝐸𝑄(𝑐̂
𝑖−1 ) + 𝑞𝑐𝑖 − 𝑆𝑖
(2.14)
При 𝑖 = 1 имеем:
𝐸𝑄(𝑐̂1 ) = 𝐸𝑄0 + 𝑞𝑐1 − 𝑆1 = 𝑄0 + 𝑞𝑐1 − 𝑆1
Отсюда следует:
𝐸𝑄(𝑐̂2 ) = 𝐸𝑄(𝑐̂1 ) + 𝑞𝑐2 − 𝑆2 = 𝑄0 + 𝑞𝑐1 − 𝑆1 + 𝑞𝑐2 − 𝑆2
= 𝑄0 + 𝑞(𝑐1 + 𝑐2 ) − (𝑆1 + 𝑆2 ) = 𝑄0 + 𝑞𝑐̂2 − (𝑆1 + 𝑆2 )
𝐸𝑄(𝑐̂3 ) = 𝐸𝑄(𝑐̂2 ) + 𝑞𝑐3 − 𝑆3 = 𝑄0 + 𝑞𝑐̂2 − (𝑆1 + 𝑆2 ) + 𝑞𝑐3 − 𝑆3
= 𝑄0 + 𝑞𝑐̂3 − (𝑆1 + 𝑆2 + 𝑆3 )
𝐸𝑄(𝑐̂4 ) = 𝐸𝑄(𝑐̂3 ) + 𝑞𝑐4 − 𝑆4 = 𝑄0 + 𝑞𝑐̂3 − (𝑆1 + 𝑆2 + 𝑆3 ) + 𝑞𝑐4 − 𝑆4
= 𝑄0 + 𝑞𝑐̂4 − (𝑆1 + 𝑆2 + 𝑆3 + 𝑆4 )
Итак, в общем случае
𝑖
𝐸𝑄(𝑐̂)
̂𝑖 − ∑ 𝑆𝑘 = 𝑄0 + 𝑞𝑐̂𝑖 + 𝑆̂𝑖
𝑖 = 𝑄0 + 𝑞𝑐
(2.15)
𝑘=1
Где 𝑆̂𝑖 = ∑𝑖𝑘=1 𝑆𝑘
Вновь воспользуемся (2.13):
2
2
𝑄2 (𝑐̂)
̂)
̂)
𝑖 = 𝑄 (𝑐̂
𝑖−1 ) + 2𝑄(𝑐̂
𝑖−1 )[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] + [𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )]
(2.16)
Из (2.16) следует:
2
𝑄2 (𝑐̂)
𝑖 − 𝑄 (𝑐̂
𝑖−1 ) =
2
= 2𝑄(𝑐̂
̂)
̂)
𝑖−1 )[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] + [𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )]
(2.17)
Применим операцию математического ожидания к обеим частям (2.17):
2
𝐸𝑄2 (𝑐̂)
𝑖 − 𝐸𝑄 (𝑐̂
𝑖−1 ) =
2
= 2𝐸𝑄(𝑐̂
̂)
̂)
𝑖−1 )[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] + 𝐸[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )]
25
(2.18)
Заметим, что
𝑄(𝑐̂)
̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 ) = [𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 𝑆𝑖
(2.19)
В то же время,
𝑖−1
𝑖−1
𝑄(𝑐̂
̂)]
𝑖−1 ) = 𝑄0 + ∑ [𝐴(𝑐̂𝑘 ) − 𝐴(𝑐
𝑘−1 − ∑ 𝑆𝑘
𝑘=1
(2.20)
𝑘=1
Из соотношений (2.19), (2.20) и свойства независимости приращений
пуассоновского процесса 𝐴(𝑡) следует, что величины 𝑄(𝑐̂
̂)
𝑖−1 ) и [𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )]
являются независимыми для любого фиксированного 𝑖. Тогда по свойству
математического ожидания
𝐸𝑄(𝑐̂
̂)
̂)
𝑖−1 )[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] = 𝐸𝑄(𝑐̂
𝑖−1 )𝐸[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )]
(2.21)
Из (2.21) с учетом (2.15) и Леммы 1 получаем формулу:
̂
𝐸𝑄(𝑐̂
̂)
𝑖−1 )[𝑄(𝑐
𝑖 − 𝑄(𝑐̂
𝑖−1 )] = [𝑄0 + 𝑞𝑐̂
𝑖−1 − 𝑆𝑖−1 ](𝑞𝑐𝑖 − 𝑆𝑖 )
(2.22)
Возведем в квадрат обе части равенства (2.19):
2
[𝑄(𝑐̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 )] =
2
2
= [𝐴(𝑐̂)
̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 2𝑆𝑖 [𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] + 𝑆𝑖
(2.23)
Применим операцию математического ожидания к обеим частям (2.23) и
воспользуемся свойством линейности математического ожидания. Тогда
2
𝐸[𝑄(𝑐̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 )] =
2
2
= 𝐸[𝐴(𝑐̂)
̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 )] − 2𝑆𝑖 𝐸[𝐴(𝑐
𝑖 − 𝐴(𝑐̂
𝑖−1 )] + 𝑆𝑖
(2.24)
Величина 𝐴(𝑐̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 ) имеет пуассоновское распределение с параметром
𝑞𝑐𝑖 . Отсюда
2
2 2
𝐸[𝐴(𝑐̂)
𝑖 − 𝐴(𝑐̂
𝑖−1 )] = 𝑞 𝑐𝑖 + 𝑞𝑐𝑖
(2.25)
Из соотношения (2.24) и (2.25) получаем:
2
2
2 2
𝐸[𝑄(𝑐̂)
𝑖 − 𝑄(𝑐̂
𝑖−1 )] = 𝑞 𝑐𝑖 + 𝑞𝑐𝑖 − 2𝑆𝑖 𝑞𝑐𝑖 + 𝑆𝑖
(2.26)
Подставив равенства (2.22) и (2.26) в соотношение (2.18), получим итоговый
результат:
2
2
2 2
̂
𝐸𝑄2 (𝑐̂)
𝑖 − 𝐸𝑄 (𝑐̂
𝑖−1 ) == 2[𝑄0 + 𝑞𝑐̂
𝑖−1 − 𝑆𝑖−1 ](𝑞𝑐𝑖 − 𝑆𝑖 ) + 𝑞 𝑐𝑖 + 𝑞𝑐𝑖 − 2𝑆𝑖 𝑞𝑐𝑖 + 𝑆𝑖
Лемма 2 доказана.
Теперь можно получить итоговый результат.
26
Теорема
2.
Математическое
ожидание
суммарной
задержки
в
рассматриваемой системе
𝐸𝑊 =
4
= ∑ 𝐸𝑊𝑖 =
𝑖=1
4
𝑐𝑖 𝑞 − 𝑆𝑖
= ∑[
𝑞 2
𝑖=1 2𝑆𝑖 (1 − )
𝑆
𝑖
2
2 2
̂
2[𝑄0 + 𝑞𝑐̂
𝑖−1 − 𝑆𝑖−1 ](𝑞𝑐𝑖 − 𝑆𝑖 ) + 𝑞 𝑐𝑖 + 𝑞𝑐𝑖 − 2𝑆𝑖 𝑞𝑐𝑖 + 𝑆𝑖
+
]
𝑞
2𝑆𝑖 (1 − 𝑆 )
𝑖
(2.27)
Доказательство.
Из Теоремы 1 с учетом утверждений Леммы 1 и Леммы 2 получаем явную
формулу для математического ожидания задержки, связанной с 𝑖 −фазой:
𝐸(𝑊𝑖 ) =
=
𝑐𝑖 𝑞 − 𝑆𝑖
𝑞 2
2𝑆𝑖 (1 − )
𝑆𝑖
2
2 2
̂
2[𝑄0 + 𝑞𝑐̂
𝑖−1 − 𝑆𝑖−1 ](𝑞𝑐𝑖 − 𝑆𝑖 ) + 𝑞 𝑐𝑖 + 𝑞𝑐𝑖 − 2𝑆𝑖 𝑞𝑐𝑖 + 𝑆𝑖
+
𝑞
2𝑆𝑖 (1 − 𝑆 )
𝑖
(2.28)
Тогда из соотношения (2.1) с учетом полученного результата (2.28) получаем
(2.27).
Теорема 2 доказана.
Утверждение Теоремы 2 представляет собой итоговый результат данного
исследования. Полученная явная формула (2.27) для средней суммарной задержки
позволяет вычислять показатель качества функционирования рассматриваемой
системы ОДД.
27
Заключение
Работа
на
математических
современном
тему
«О
моделей
мегаполисе»
некоторых
проблемах
функционирования
посвящена
построения
регулируемого
созданию
и
и
анализа
перекрестка
исследованию
в
модели
организации дорожного движения на регулируемом пересечении Ленинского
проспекта и улицы Обручева в г. Москве.
В первой части работы приведен обзор и краткий анализ результатов,
связанных с исследованием и разработкой математических моделей динамики
автотранспортного потока.
В основной части за основу исследования был взят существующий результат
микроскопического моделирования американского ученого МакНила [11] для
двухфазной системы регулирования движения на перекрестке.
В настоящей работе построена и исследована более сложная четырехфазная
модель ОДД на перекрестке. В результате анализа получена явная формула для
важного показателя – математического ожидания суммарной задержки в системе.
Данный показатель может служить характеристикой качества ОДД в системе.
Отметим, что данное исследование было выполнено на базе реальной
системы, а именно, системы ОДД перекрестка Ленинского проспекта и улицы
Обручева. Однако теоретические результаты, полученные в работе, могут быть
использованы и для анализа других систем ОДД в крупных современных городах.
28
Список литературы
[1] Гасников А. В., Кленов С. Л., Нурминский Е. А., Холодов Я. А., Шамрай
Н. Б. Введение в математическое моделирование транспортных потоков под
ред. А. В. Гасникова, с приложениями М.Л. Бланка, Е.В. Гасниковой, А.А.
Замятина, В.А. Малышева, А.В. Колесникова, А.М. Райгородского. – МФТИ,
2010
[2] Дубелир Г.Д. Планировка городов. - СПБ, 1910
[3] Дубелир Г.Д., Корнеев Б.Г., Кудрявцев М.Н. Основы проектирования
автомобильных дорог. – М., Л.: Изд-во Наркомхоза РСФСР, 1938
[4] Ивченко Г.И., Каштанов В.А., Коваленко И.Н. Теория массового
обслуживания: Учеб. пособие для вузов. – М.: Высш. школа, 1982
[5] Иносэ Х., Хамада Т. Управление дорожным движением. М.: Транспорт, 1983
[6] Левашев А. Г., Михайлов А. Ю., Головных И. М. Проектирование
регулируемых пересечений. - Учеб. Пособие – Иркутск: Изд-во ИрГТУ, 2007
[7] Липцер Р. Ш., Ширяев А. Н. Статистика случайных процессов. Нелинейная
фильтрация и смежные вопросы. - М., Изд-во Наука, 1974
[8] Маталыцкий М.А., Тихоненко О.М., Косарева Е.В. Анализ и применения
систем и сетей массового обслуживания. -ГрГУ им. Я. Купалы, 2013
[9] Сысоев А.С. Моделирование и оптимизация систем с переменной структурой
методами идемпотентной математики и анализа конечных изменений: Дисс.
–Липецк, 2013
[10]
Adams W. F. Road traffic considered as a random series. – J. Inst. Civil
Engineers. 1936, vol. 4
[11]
Donald R. McNeil. A Solution to the Fixed-Cycle Traffic Light Problem for
Compound Poisson Arrivals. – Journal of Applied Probability, Vol. 5, No. 3 (Dec.,
1968)
[12]
Edited by Gartner N.H., Messer C. J., Rathi A.K. Traffic flow theory: A state-
of-the-art report. -Washington DC: Transportation Research Board, 2001
29
[13]
Greenberg H. An analysis of traffic flow. – Opns. res., 1959, vol.7
[14]
Greenshields B. A study of traffic capacity.– Proc. (US) highway research,
board, 1934, vol. 14
[15]
Hongjun Zhang, Stephen G. Ritchie. An integrated traffic responsive ramp
control strategy via nonlinear state feedback. – Institute of transportation studies
university of California, Irvine. 1995
[16]
Lighthill M.J., Whitham G. B. On kinematic waves: II. – Proc. R. Soc.
London, Ser. A. 1955, vol. 5.
[17]
Nagel K., Schreckenberg M. A cellular automation model for freeway traffic.
– Phys. I France. 1992. Vol. 2
[18]
Newell G.F. Nonlinear effects in the dynamics of car following. – Opns. Res.
1961, vol. 9
[19]
Payne H.J. Models of freeway traffic and control.– Simulation Council Proc.
28, Mathematical Models of Public Systems. Edited by G.A. Be key. 1971, vol. 1
[20]
Richards P.I. Shock waves on the Highway. – Opns. Res. 1956, vol. 5
[21]
Анатолий Темкин, Иван Голунов.: Максим Ликсутов – РБК: «Надо
дать возможность людям легально парковаться». – РБКdaily,URL:http://daily.rbc.ru/interview/business/09/02/2015/54d73d849a7947745a9
0bb71#xtor=AL-%5Binternal_traffic%5D--%5Bm.rbc.ru_tablet%5D%5Bmain_body%5D-%5Bitem_11%5D
30